Рассмотрим несколько режимов, каждый из которых определяется конкретными схемой соединения обмоток трансформатора, исполнением линии, загрузкой трансформатора и т.д. Для каждого из рассматриваемых режимов изменяется спектр высших гармоник тока и соответствующий ему спектр высших гармоник напряжения. Кроме того, изменяется эквивалентное сопротивление сети для n-й гармоники Z(n), которая определяется сопротивлениями конкретных элементов сети. Очевидно, что в сетях НН точно определить значения коэффициента искажения синусоидальности кривой напряжения КU, не зная значения гармоник тока, генерируемых конкретной нелинейной нагрузкой в конкретном режиме, не представляется возможным.
В работе [40] рассмотрено, как изменяются высшие гармоники при изменении схемы соединения обмоток трансформатора. Если мы рассчитаем с помощью точной модели значения КU для сети НН с трансформатором, обмотки которого соединены по схеме звезда—зигзаг с нулем, то увидим, что они будут соответствовать верхней кривой (расчет), показанной на рис. 2.14. Известно, что при соединении обмоток по такой схеме сопротивление нулевой последовательности трансформатора Ζτ на порядок меньше соответствующего сопротивления при соединении обмоток по схеме звезда—звезда с нулем. В результате уменьшается значение Z(n=3k) для данного режима. Если мы используем выражения (2.9) и (2.10) для определения напряжений высших гармоник, подставляя известные значения I(n), посчитанные для
сети НН с трансформатором, обмотки которого соединены по схеме звезда—звезда с нулем, и вновь рассчитанные значения Z(n), то получаем значения ΚU, зависимость которых от а показана на рис. 2.14 кривой 2 (предположение).
Из рисунка видно, что расчетные значения ΚU превышают предполагаемые в 1,6—1,8 раза. Это вызвано возросшей амплитудой токов высших гармоник (особенно кратных трем) при использовании трансформатора со схемой соединения обмоток звезда-зигзаг с нулем.
Рис. 2.14. Уменьшение значения Κ в случае неправильного учета изменения схемы соединения обмоток трансформатора: 1— расчет; 2— предположение
Рис. 2.15. Уменьшение значения Κ в случае неправильного учета изменения коэффициента загрузки трансформатора: 1 — расчет; 2 — предположение
Таким образом, применение традиционных моделей для определения напряжений высших гармоник в сети НН с трансформатором, обмотки которого соединены по этой схеме, на основании имеющейся информации о значении высших гармоник тока, генерируемых данной нелинейной нагрузкой в случае использования трансформатора со схемой соединения обмоток звезда—звезда с нулем, приводит к неверным результатам. При этом амплитудные значения и фазы напряжений отдельных гармоник значительно отличаются от рассчитанных с помощью точной модели.
Проанализируем возможность использования выражений (2.9) и (2.10) для определения напряжений высших гармоник при разных значениях коэффициента загрузки трансформатора β. На рис. 2.15 показаны зависимости Κ от а при β = 0,8 и β = 0,4, причем две верхние кривые (расчет) построены с учетом результатов, полученных путем точного моделирования данных нагрузочных режимов, а две нижние кривые (предположение) — с учетом значения токов высших гармоник, которое скорректировано в соответствии с β. При этом предположении нелинейная нагрузка представлялась источником токов высших гармоник
где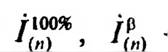
— ток п-й гармоники для случаев 100%-ной загрузки трансформатора и предполагаемой загрузки трансформатора, определяемой β.
Из рис. 2.15 видно, что при снижении β увеличивается ошибка от расчета с учетом предполагаемых значений. Если при β = 0,8 расчетные значения Κ превышают предполагаемые в 1,1—1,2 раза, то при β = 0,4 — в 1,8—2,1 раза. Как и в предыдущем случае, амплитудные значения отдельных гармоник напряжения, рассчитанные двумя методами, различаются в несколько раз.
Полученные результаты можно объяснить следующим образом. Каждый конкретный режим определяется конкретным соотношением параметров сети и нагрузки и, как следствие, характером протекания электромагнитных процессов. В результате каждый конкретный режим подключения нелинейной нагрузки к низковольтной сети характеризуется определенным искажением форм кривых как тока, так и напряжения и, следовательно, определенным значением их высших гармоник. В связи с этим формально использовать выражения (2.9) и (2.10) для нахождения значений напряжений высших гармоник одного режима по значениям токов высших гармоник других режимов (даже очень близких) в целях проведения точного анализа не представляется возможным.
Таким образом, с учетом изложенного выше, схемы замещения сети НН с нелинейной нагрузкой, в которых данная нагрузка представляется источниками токов высших гармоник можно использовать для разработки приближенных оценочных методик. С помощью таких методик можно, в частности, проводить общий анализ влияния нелинейных нагрузок на форму кривых токов и напряжений в трехфазных сетях с нулевым проводом. Для проведения данного анализа необходимо определить зависимость между коэффициентом «-й гармонической составляющей напряжения в виде Кт = UM/UHOM и коэффициентом гармонической составляющей тока в виде К действующие значения тока и напряжения номинальных фазных и п-й гармоники соответственно) для конкретной сети. Упростив выражение (2.8) переходом к действующим значениям тока и напряжения и подставив в него выраженные через К, получим
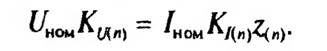
Разделив левую и правую части на Iном, найдем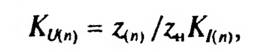 
где z — полное сопротивление нагрузки, z(n) — полное сопротивление сети для п-й гармоники.
Для определения полного сопротивления нагрузки находим:
- Полное, активное и индуктивное сопротивления фазы сети
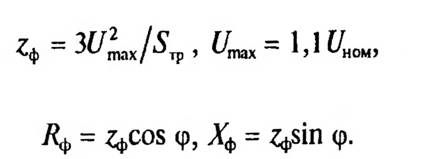
- Активное и индуктивное сопротивления фазных продольных элементов сети
- Активное, индуктивное и полное сопротивления нагрузки
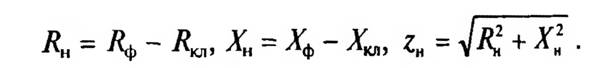
Обозначив Z|Zh = А(n) получим
Таким образом, зная значения zH для конкретной сети, мы можем определять зависимость K в этой сети, не конкретизируя нелинейную нагрузку.
В качестве примера рассмотрим сеть НН, которая представлена трансформатором мощностью 25 кВ А (схема соединения обмоток звезда—звезда с нулем), кабельной линией сечением 3x25+1x10 мм2 длиной 0,2 км и нагрузкой, являющейся источником токов высших гармоник, причем cos φ = 0,95. Тогда сопротивления элементов схемы замещения (Ом) такие:
В результате расчета получаем z= 5,941 Ом, а значения можно найти из выражений (2.9) и (2.10).
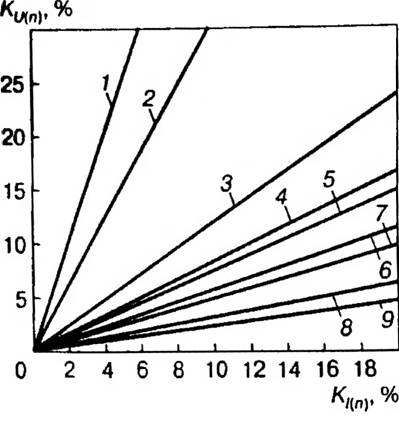
Рис. 2.16. Зависимости К для одного из конкретных вариантов исполнения сети НН
Тогда для данного варианта сети НН получаем следующие значения коэффициентов А(п) для одного из вариантов сети НН:
Очевидно, что значения в общем случае существенно превышают А. В соответствии с этим, напряжения гармоник, кратных трем, являются определяющими для суммарного напряжения высших гармоник даже при небольших значениях соответствующих составляющих токов. При одинаковом относительном увеличении токов всех гармоник напряжения возрастают значительно быстрее напряжений U. На рис. 2.16 показаны зависимости К для рассматриваемых гармоник. Из представленных графиков видно, что при K= 10 % К =11,84 %, а при К(5) = 10 %, Ки(5) - 2,26 %. Если соответствующий Кп(3) возрастает до 20%, то увеличивается до 23,68%, а К(5) — только до 4,52%. Согласно ГОСТ 13109—97 нормально допустимое значение К при n= 3 равно 5%, а при 5 — 6%. Из графиков (рис. 2.16) видно, что для выполнения этого условия в рассматриваемой сети К(3) не должен превышать 4,22%. Для сравнения: требования ГОСТ 13109—97 для высших гармоник с n= 5 в этом случае выполняются при К(5) < 26,51 %.
Таким образом, полученные кривые наглядно показывают, что даже низкий уровень токов гармоник, кратных трем (единицы процентов), может привести к значительным искажениям напряжений. Вместе с тем даже большие значения токов гармоник с n=2k(десятки процентов) часто не приводят к нарушению требований ГОСТ 13109—97 к значению.
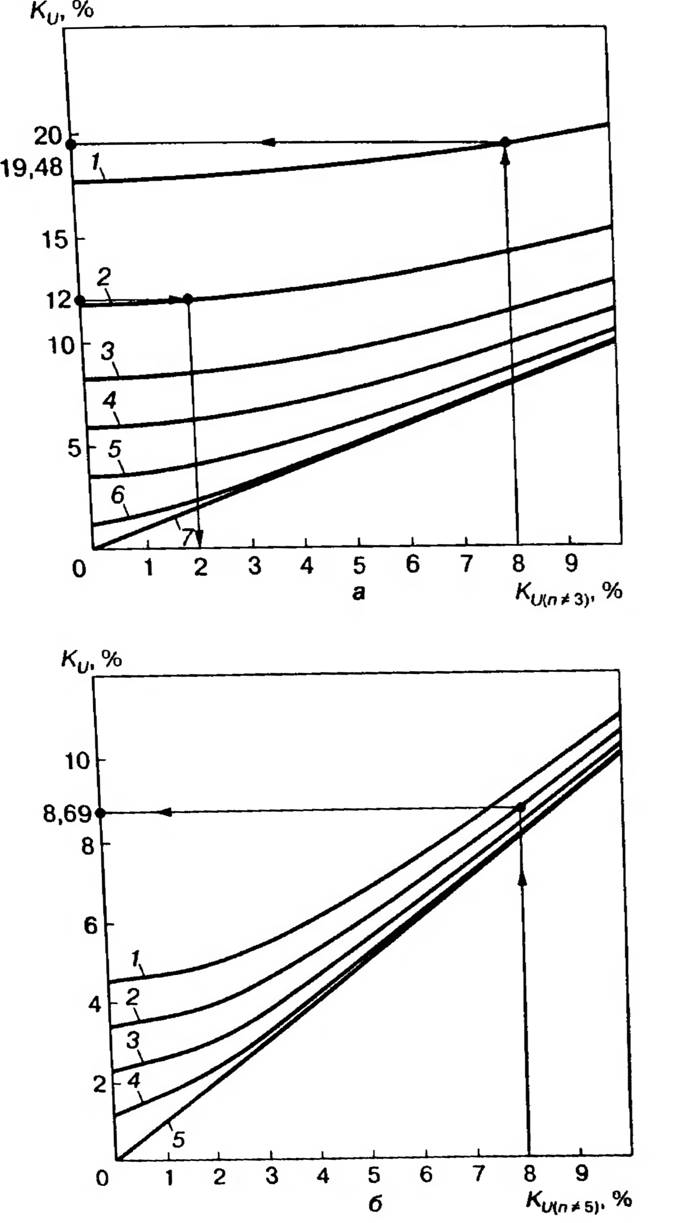
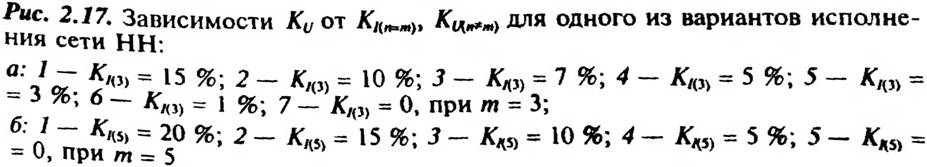
Наличие гармоник с n= 3k в спектре высших гармоник тока является определяющим фактором для коэффициента искажения синусоидальности кривой напряжения. На рис. 2.17, показаны зависимости
соответственно для случаев т = 3 и т = 5, где коэффициент искажения синусоидальности кривой напряжения с учетом всех гармоник, кроме п = т. Семейство кривых для заданных гармоник описывается выражением
С помощью указанных графиков легко определить, как токи разных гармоник влияют на значение Ки. Анализ графиков показывает, что, например, увеличение коэффициента искажения синусоидальности кривой напряжения за счет третьей гармоники тока при К(3) =3 % (рис. 2.17,а) можно сравнить с увеличением Κu за счет пятой гармоники тока при К(5) = 15 % (рис. 2.17, б).
Продолжая анализ, можно легко показать на графиках, что за счет третьей гармоники тока ( К0) = 15 %) Ки увеличивается от 8 до 19,48 % (рис. 2.17, а), а за счет пятой гармоники тока (К1(5)= 15 %) Кu изменяется от 8 до 8,69 %, т.е. увеличение составляет только 0,69 % (рис. 2.17, б). Рассмотрим случай (рис. 2.17, а), когда Κu = 12 %, причем известно, что К(3) =10 %. Из рисунка видно, что несинусоидальность напряжения, вызываемая остальными гармониками, будет определяться значением KU = 2 %. Из рис. 2.17, б следует, что при 8 пятая гармоника тока (Kl(5)= 10 %) почти не влияет на коэффициент искажения синусоидальности кривой напряжения.
Покажем с помощью рассматриваемых графиков, как это свойство трехфазных четырехпроводных сетей, которое заключается в преобладающем влиянии гармоник, кратных трем, можно использовать на практике. Очевидно, что, фильтруя токи указанных гармоник, можно значительно снизить несинусоидальность напряжения. Это предполагает применение фильтров токов гармоник, кратных трем, в качестве эффективного средства снижения искажений формы кривых напряжений в трехфазных сетях с нулевым проводом. Следует отметить, что для конкретной сети всегда можно построить графики, аналогичные показанным на рис. 2.17, и с их помощью, зная значения Ки и КI(n=3к), определить значение KU(n). В результате можно заранее сделать вывод об эффективности фильтрации высших гармоник с помощью упомянутых фильтров в данной сети.
Например, для рассматриваемого варианта сети (см. рис. 2.17, а) при К(3) =15 % полная фильтрация тока третьей гармоники может привести к значению Κ< 8 % (по ГОСТ 13109—97) в случае, если до фильтрации коэффициент искажения синусоидальности кривой напряжения был не больше 19,5%.
Очевидно, что искажение формы кривой тока, вызываемое нелинейной нагрузкой, можно определять коэффициентом искажения синусоидальности кривой тока выражая его через коэффициенты п-х гармонических составляющих тока:
где N - порядок последней из учитываемых гармоник тока.
Исходя из предыдущих выводов, можно предположить, что КI не является показателем, который однозначно характеризует влияние нелинейной нагрузки на форму кривой напряжения сети. Очевидно, что при постоянном К, значение К в каждом конкретном случае для различных гармоник может существенно различаться, что в свою очередь приведет к разным значениям Κu.
Покажем это на примере рассматриваемого варианта сети НН. Для простоты считаем, что нелинейная нагрузка вызывает появление только третьей, пятой и седьмой гармоник тока. Пусть К, = const = 14,14 %, а значение К1(п) для этих трех гармоник изменяется и может принимать одно из значений: 6,8 или 10 %. В результате Ки при различных значениях К(n) изменяет свое значение от 7,86 до 12,17 %.
Зависимости Ки от значения К(п) для гармоник с л = 3, 5, 7 описываются выражением
Поскольку К, = const, то, например, для каждой пары значений K(5) и КI(7) однозначно находится К(3) из выражения
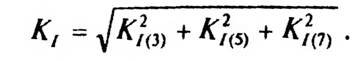
Аналогично по имеющимся значениям К можно находить Кт.
Очевидно, что при постоянном К= 14,14 % и изменяюoихся в широких пределах К(п) (от 0 до 14,14 %) интервал изменения очень велик — от 3,2 до 16,8 %. Меньшему значению Ки соответствует вариант, когда все искажение формы кривой напряжения вызвано током пятой гармоники при К(5)=14,14 %. Большее значение Ки = 16,8 %получается при K(3) = 14,14 %, Κ = 0 и К = 0.
Таким образом, показано, что при одном и том же значении К, значение Ки определяется количественным и качественным составом спектра высших гармоник тока нелинейной нагрузки и может принимать самые разные значения. При этом, как отмечалось ранее, определяющим фактором является значение токов гармоник, кратных трем. Это обстоятельство следует учитывать как при разработке фильтрующих устройств, так и при проектировании оборудования, которое является источником высших гармоник тока. Следовательно, при минимизации К, входного тока данной нелинейной нагрузки необходимо в первую очередь (если есть такая возможность) снижать уровень гармоник, кратных трем, причем в этом случае можно допустить увеличение уровня других гармоник и даже K.
На основании изложенного выше можно сделать вывод, что с помощью моделей сетей НН, в которых нелинейная нагрузка задается источниками токов высших гармоник, удобно проводить анализ зависимостей высших гармоник тока и напряжения. При этом, не конкретизируя нелинейную нагрузку, можно рассматривать конкретную низковольтную сеть с определенными параметрами. Предложенный метод дает возможность готовить демонстрационные или учебные материалы, а также разрабатывать соответствующие методики, позволяющие оценить уровень высших гармоник и определить некоторые закономерности для трехфазных сетей с нулевым проводом, например, наглядно показать доминирующее влияние гармоник, кратных трем. При этом можно, в частности, предложить направление оптимизации и рекомендовать средства снижения уровня высших гармоник.
