Несмотря на указанные ограничения, касающиеся области применения рассмотренной в предыдущем параграфе математической модели, полученные с ее помощью результаты достаточно точны, а достоверность их проверена на физической модели и не вызывает сомнения. Однако в инженерной практике часто возникает необходимость проведения оценочных, довольно приближенных, но удовлетворяющих по точности и, в то же время, не требующих разработки сложных математических моделей и привлечения компьютерной техники расчетов. В этом смысле традиционные модели, в которых нелинейная нагрузка задается источником тока n-й гармоники, представляют несомненный интерес.
Рассмотрим возможность использования подобных моделей для сетей НН. Как было отмечено в параграфе 2.2, при использовании этих моделей в трехпроводных сетях значение тока n-й гармоники находится при условии подключения данной нелинейной нагрузки к сети бесконечной мощности. Искажение синусоидальности кривой напряжения при этом определяется падениями напряжения от соответствующих токов высших гармоник на сопротивлениях продольных элементов сети. В случае трехфазной четырехпроводной сети путь протекания токов гармоник, кратных трем, отличается от пути протекания токов остальных гармоник. В соответствии с этим при условии симметрии нагрузок однолинейные схемы замещения могут быть двух видов. На рис. 2.8,а показана схема замещения сети для гармоник, некратных трем, кратных трем В этих схемах нелинейная нагрузка представлена источником тока n-й гармоники.
Здесь Ζκ(n) и ΖΤ(n) — сопротивления короткого замыкания и нулевой последовательности трансформатора для n-й гармоники;
Ζ(n) и Ζ0(n) — сопротивления фазного и нулевого проводов линии для n-й гармоники; I(n) и U(n) — ток и напряжение сети n-й гармоники, причем
 (2.8)
(2.8)

Рис. 2.8. Однолинейные схемы замещения сети НН с источником тока n-й гармоники
где Z(n) — эквивалентное сопротивление сети для n-й гармоники. Очевидно, что напряжение гармоник, некратных трем, имеет вид ![]()
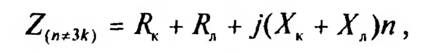
а напряжение гармоник, кратных трем, представлено в виде

Вначале убедимся, что без адаптации традиционных моделей к особенностям сетей НН, их применение для анализа рассматриваемой низковольтной сети невозможно. Зная токи высших гармоник, полученные при условии питания выпрямителя от сети бесконечной мощности, и значения соответствующих эквивалентных сопротивлений сети, с помощью выражений (2.9) и (2.10) можно определить значения напряжений этих гармоник и Кu. На рис. 2.9 показаны зависимости КU(n) и КU от а для выпрямителя с постоянной времени RС-цепи τ = 0,075 с и параметров рассматриваемого в параграфе 2.2 варианта сети НН, полученные с помощью традиционного подхода. Из рисунка видно, что напряжения рассматриваемых гармоник весьма значительны. В результате коэффициент искажения синусоидальности кривой напряжения достигает при а = 0,9 значения 289,6 %. Очевидно, что этот уровень гармоник напряжения в реальной сети невозможен, т.е. такой расчет гармоник напряжения в сетях НН с помощью традиционных моделей приводит к неверным результатам.
Внесем определенные коррективы в расчетный механизм, чтобы адаптировать данные модели к особенностям сетей НН и получить возможность применения традиционных схем замещения для инженерных расчетов. Как уже отмечалось, при подключении выпрямителя к конкретной сети НН значение высших гармоник уменьшается по сравнению с посчитанными при условии питания от сети бесконечной мощности. Предположим, что в схемах замещения (рис.2.8) источник тока n-й гармоники генерирует токи высших гармоник, значение которых соответствует посчитанным с учетом параметров сети; при этом эквивалентное сопротивление сети для п-й гармоники остается прежней. Определим напряжения высших гармоник с помощью выражений (2.9) и (2.10).

Рис. 2.9. Зависимости ΚU и КU(n) от а в случае использования традиционных моделей без адаптации к особенностям сети НН:
1 — Кu, 2 — КU(9); 3 — КU(3); 4 — КU(7), 5 — Кu(11),
Полученные в результате расчета значения напряжений высших гармоник с высокой точностью совпадают со значениями соответствующих напряжений, полученных с помощью модели, учитывающей параметры нагрузки и сети.
Следует отметить, что наилучшее совпадение наблюдается для напряжений гармоник с п < 13, для которых относительная погрешность составляет менее 5 %. Таким образом, традиционные однолинейные схемы замещения, в которых нелинейная нагрузка задается источниками тока высших гармоник, можно использовать для определения с достаточной для инженерных расчетов точностью напряжений высших гармоник в сетях НН. Для этого токи высших гармоник или форму их кривых (которую, в частности, можно получить экспериментально) необходимо приводить в соответствие с конкретной сетью НН.
Аналогично можно использовать и трехфазные схемы замещения сети НН, которые учитывают указанные ранее особенности ее построения. В работе [121] рассмотрена такая схема замещения сети НН с нелинейными нагрузками, представленными источниками тока произвольной формы (рис. 2.10). При этом для простоты индуктивные элементы сети и нагрузки не учитываются. На рисунке eA(t), e(t), e — трехфазная симметричная система ЭДС, R -RN — сопротивления фазных и нулевого проводов линии; Ra, Rb, Rc — три произвольных нагрузочных сопротивления, параллельно которым подключаются нелинейные нагрузки (источники тока); iA(t), i(t), i(t) — токи в фазных и нулевом проводе линии; fa(t), Ih(t), — фазные токи нелинейных нагрузок; i(t), i2(t), i3(t) — фазные токи в нагрузочных сопротивлениях.
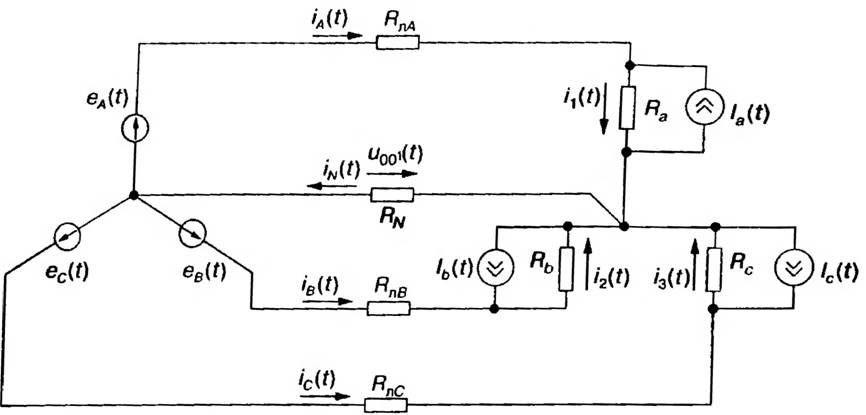
Рис. 2.10. Трехфазная схема замещения сети НН с источниками токов нелинейных нагрузок
Математическая модель, рассмотренная в предыдущем параграфе, использовалась для численного расчета токов и напряжений в сети НН. В работе [121] были получены аналитические выражения для режимных параметров низковольтной сети с нелинейными нагрузками без учета индуктивности элементов.
Для схемы (рис. 2.10) по методу узловых напряжений (при эквивалентной замене источников тока источниками ЭДС) запишем уравнение в виде: 
Из приведенного уравнения находим падение напряжения в нулевом проводе:

Как и прежде, в качестве нелинейной нагрузки в схеме замещения сети НН рассматриваем идеализированный однофазный выпрямитель, схема которого приведена на рис. 2.5. Известно, что поведение этой схемы, обусловленное процессами заряда и разряда конденсатора фильтра, характеризуется импульсным режимом работы выпрямителя. Это означает, что если на вход указанной схемы подается напряжение u(l) = Umsin ωt, то ее входной ток I(t) будет иметь импульсный характер с большим содержанием высших гармоник. В связи с этим представим входной ток рассматриваемого нелинейного электроприемника в виде:

Следует отметить, что выражение (2.14) лишь отражает импульсный характер рассматриваемого входного тока, гармонический спектр которого, как известно, содержит нечетные гармоники, соизмеримые по значению с первой. Поэтому данное представление его кривой не претендует на высокую точность, но с методической точки зрения представляется вполне корректным. Например, в работе [117] такое же представление входного тока выпрямителя с емкостным фильтром используется при моделировании его выходного напряжения в установившихся и переходных режимах.
Тогда с учетом (2.14) для фазных составляющих источника тока принимаем

Трехфазная система ЭДС задается в виде 
В соответствии с параметрами рассматриваемого варианта сети НН с помощью формул (2.11)—(2.16) были проведены расчеты режимных параметров, графики которых приведены на рис. 2.11 (входной ток выпрямителя), на рис. 2.12 (ток в фазном проводе линии), на рис. 2.13 (ток в нулевом проводе линии).
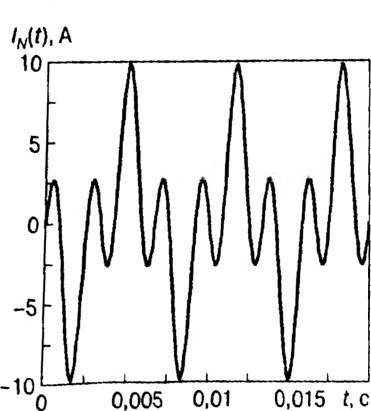
Рис. 2.13. Ток в нулевом проводе линии
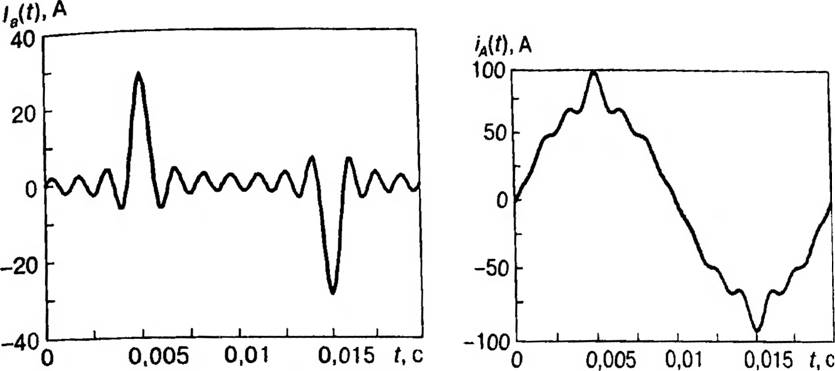
Рис. 2.12. Ток в фазном проводе линии
Рис. 2.11. Входной ток однофазного выпрямителя

Анализ данных результатов показал их определенное отличие от результатов, полученных с помощью точной модели. Очевидно, что это отличие определяется точностью представления тока нелинейной нагрузки в виде определенного аналитического выражения или точностью его приведения в соответствие с конкретной сетью НН. Более точные результаты можно вероятно ожидать при использовании экспериментально полученных осциллограмм кривых токов нелинейных нагрузок. Поэтому найденные аналитические характеристики можно использовать в дальнейших исследованиях для приближенного анализа электромагнитных процессов в сетях НН с нелинейными нагрузками.

