Глава вторая
МОДЕЛИРОВАНИЕ И АНАЛИЗ РЕЖИМОВ СЕТЕЙ НИЗКОГО НАПРЯЖЕНИЯ С НЕЛИНЕЙНЫМИ НАГРУЗКАМИ
Моделирование нелинейных нагрузок
Адекватность моделирования режима СЭС во многом определяется принятой моделью нагрузки [93]. Моделированию нелинейных нагрузок посвящен ряд работ отечественных и зарубежных ученых. Широко распространены модели, в которых нелинейные нагрузки определяются либо нелинейными вольт-амперными характеристиками, которые аппроксимируются различными функциями, либо нелинейными сопротивлениями (проводимостями), управляемыми напряжениями с заданными вольт-амперными характеристиками. Например, в работах [163, 164] анализируются и синтезируются корректирующие устройства для уравновешивания режимов в цепях с нелинейными нагрузками, характеристики которых аппроксимируются степенным полиномом. В работе [159] анализируются нелинейные электрические цепи постоянного и переменного токов, в которых нелинейные зависимости сопротивления нагрузки от тока или напряжения аппроксимируются, в частности, укороченным полиномом второй степени. В работе [19] математические модели нелинейных элементов в виде нелинейных проводимостей с заданным законом изменения использованы для расчета потокораспределения электроэнергетической системы. При этом в одних случаях рассматривается сеть бесконечной мощности, а в других — учитываются параметры сети. Однако описанные в этих работах модели нелинейных нагрузок непригодны для анализа электромагнитных процессов в питающей сети.
Известно, что преобразовательная техника является главным источником высших гармоник в современных СЭС. В настоящее время широко применяются модели полупроводниковых преобразователей (ПП), позволяющие исследовать и оптимизировать электромагнитные процессы, протекающие в их силовых цепях.
При этом модели и реализующие их комплексы программ могут быть как достаточно сложными, так и простыми (макромодели) [20] с точки зрения объема вычислений и затрат машинной памяти. Сложные универсальные модели вентильных преобразователей позволяют производить анализ установившихся и переходных процессов, вычислять значения токов и напряжений, установленные мощности во всех элементах цепи, исследовать различные режимы работы (наброс и сброс нагрузки, короткое замыкание и др.), выбирать параметры и настраивать системы авторегулирования, проводить гармонический анализ токов и напряжений на элементах и т.д.
Для проведения конкретных исследований определенного преобразователя используют макромодели полупроводниковых преобразователей, т.е. упрощенные модели, позволяющие решить задачу при сохранении достаточной для практики точности моделирования. Одной из конкретных задач является гармонический анализ кривой входного тока преобразователя. Известны модели, позволяющие определить гармоническое содержание кривой входного тока, различных видов преобразователей, в частности выпрямителей [58, 85, 161, 210]. Преимуществом подобных моделей является то, что величина высших гармоник определяется в зависимости от параметров конкретного преобразователя. Например, чаше всего встречающиеся шестипульсные выпрямительные системы образуют гармонические составляющие кривой тока порядка п= 6(k+ 1) ± 1, где к =0, 1, 2, 3,... Причем вопрос о доле этих гармонических составляющих в кривой тока, питающего выпрямитель, весьма сложный, так как она является функцией не только числа пульсаций, но и выпрямленного напряжения и параметров цепи выпрямителя. Кроме того, такие макромодели ПП позволяют анализировать электромагнитные процессы в их силовых цепях.
Одна из наиболее распространенных многофазных схем выпрямителей — это трехфазная мостовая схема. Общеизвестна проблема ухудшения КЭ, вызываемая несинусоидальным характером тока, потребляемого из сети нелинейными нагрузками типа трехфазного выпрямителя с емкостным фильтром [52]. Применительно к частотно регулируемому асинхронному электроприводу эта проблема в широком плане рассмотрена в [26]. В работе [25] приведены экспериментальные и расчетные характеристики фазных токов упомянутых выпрямителей. При этом расчеты проводились с помощью цифровой модели средствами пакета программ Microsim Design Lab 8.0 (PSpice).

Рис. 2.1. Трехфазная мостовая схема выпрямителя с емкостным фильтром
В работе [118] исследована математическая (аналитическая) модель трехфазных мостовых выпрямителей с применением коммутационных функций. На рис. 2.1 представлена трехфазная мостовая схема выпрямления. Здесь неуправляемый выпрямитель DI...D6 подключен к сети с трехфазной системой питающих напряжений uA(t), u(t), U(t).
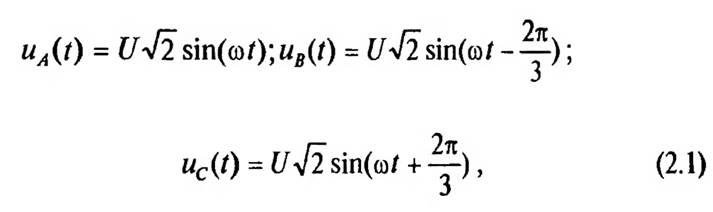
где ω = 314 — угловая частота; t — время; 220В — действующее значение фазного напряжения. Кроме того, на рисунке Сф — фильтрующий конденсатор; R — активная нагрузка; iA(t), i(t) — мгновенные значения токов на входе выпрямителя; iф(t), i(t) — мгновенные значения токов, протекающих в емкости фильтра и нагрузке; u(t), i — мгновенные значения выпрямленных напряжения и тока на выходе выпрямителя.
Известно [108], что математическая связь между мгновенными значениями входных и выходных электрических величин вентильного коммутатора выражается с помощью коммутационных функций следующим образом:
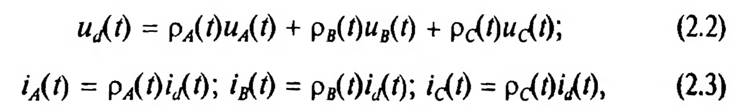
где ρΑ(ί), Рв(0» Рс(0 — коммутационные функции трехфазного выпрямителя. График изменения р^(г) приведен на рис. 2.2 для случая мгновенной коммутации вентилей и угла управления а = 0.

Рис. 2.2. Коммутационная функция для фазы А трехфазного выпрямителя
Рис. 2.3. Выпрямленное напряжение на выходе трехфазного выпрямителя
Аналитически функции p можно аппроксимировать следующим образом:
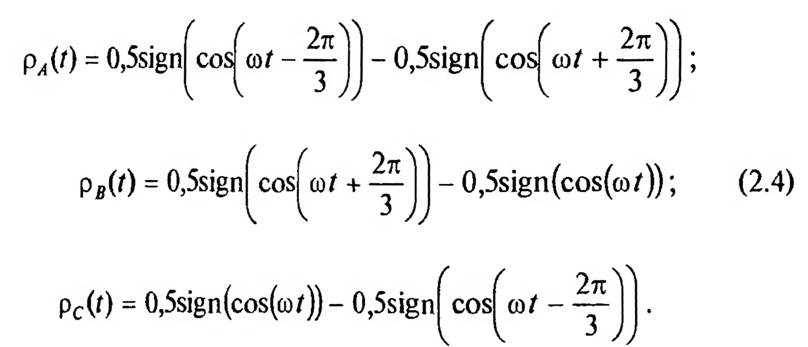
Согласно выражениям (2.1), (2.2) и (2.4) для выпрямленного напряжения ud(t) имеем график, представленный на рис. 2.3.
Функция, показанная на рисунке, аппроксимируется выражением
![]()
Запишем дифференциальное уравнение для RC -цепи выпрямителя:
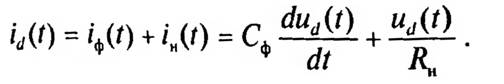
Тогда с учетом выражения (2.5) мгновенное значение выпрямленного тока такое:
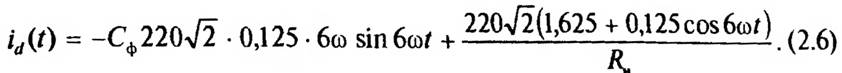
Мгновенные значения фазных токов, потребляемых схемой из сети, определяются с учетом формул (2.3) и (2.6):
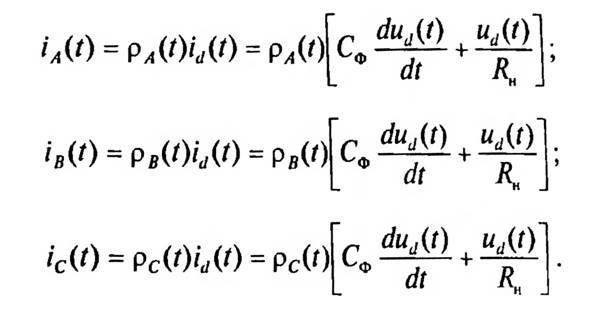
График изменения фазного тока iA(t) при значениях емкости Сф = 100 мкФ и сопротивления RH = 66 Ом приведен на рис. 2.4. Данная кривая (рис. 2.4) может быть аппроксимирована с определенной точностью (с учетом погрешности, которая возникает из-за приближенного выбора коммутационной функции) тригонометрическим полиномом вида


Рис. 2.4. Фазный ток на входе трехфазного выпрямителя
Из выражения (2.7) видно, что спектр гармоник потребляемого тока содержит пятую и седьмую гармоники, составляющие соответственно 90 % и 85 % основной, что соответствует результатам гармонического анализа фазных токов трехфазных мостовых выпрямителей с емкостным фильтром, полученным в работе [25]. Таким образом, корректность проведенного аналитического моделирования подтверждается результатами, полученными с помощью цифровой модели.
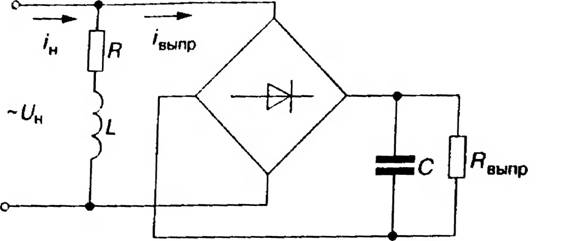
Рис. 2.3. Однофазный выпрямитель, включенный параллельно активно-индуктивной нагрузке
В сетях НН широко распространены однофазные выпрямительные нагрузки небольшой мощности, в частности, компьютеры, телекоммуникационная аппаратура, аудио- и видеотехника, бытовые электроприборы, а также источники питания различных электротехнических установок. Очевидно, что для указанных однофазных нагрузок можно построить модели (аналогичные рассмотренным трехфазным), позволяющие проводить гармонический анализ их входных токов. Например, в работе [123] предлагается аналитический способ определения входных и выходных токов однофазных мостовых преобразователей, который основывается на использовании параметров холостого хода T-образной схемы замещения преобразователя. В работе [2] представлены результаты численного моделирования средствами пакета программ PSpice ORCAD 9.2 Trial разных однофазных схем питания частотнорегулируемых приводов.
На рис. 2.5 показан однофазный выпрямитель с емкостным фильтром, включенный параллельно активно-индуктивной нагрузке и питающийся от сети бесконечной мощности напряжением Uном = 220 В. Пусть параметры этой суммарной нагрузки (в соответствии с вариантом, анализируемым в [48]) имеют следующие значения: R = 3,6 Ом; L = 21,5 мГн; Iвыпр = 29,31 Ом; С =2,56х10-3 Ф. При этом мощность выпрямителя Рвыпр = 3,035 кВт, а доля выпрямительной нагрузки а = Рвыпр/Рн = 0,5 суммарная активная мощность нагрузки).
Проведенные расчеты показывают, что ток выпрямителя с емкостным фильтром имеет ярко выраженный импульсный характер с большим содержанием высших гармоник. В результате коэффициент искажения синусоидальности кривой тока выпрямителя Квыпр = 168,53 %. Суммарный ток нагрузки содержит все гармоники входного тока выпрямителя, но К1н = 70,47 %, так как его первая гармоника больше. Ток активно-индуктивной нагрузки имеет синусоидальную форму, поскольку при питании от сети бесконечной мощности на него не влияет выпрямительная нагрузка.
Таким образом, рассмотренные модели позволяют проводить расчет высших гармоник тока с учетом характерных параметров нелинейных электроприемников. Однако, главным с точки зрения проведения исследований ЭМС недостатком рассмотренных моделей является то, что искажение синусоидальности кривой входного тока ПГТ определяется при условии питания его от сети бесконечной мощности. При этом получают спектр гармоник тока без учета обратного воздействия на них параметров сети, а искажение синусоидальности кривой питающего напряжения не рассматривают.

