Глава третья
УСОВЕРШЕНСТВОВАНИЕ МОДЕЛЕЙ И РАСЧЕТ НЕСИНУСОИДАЛЬНОСТИ ТОКОВ И НАПРЯЖЕНИЙ НИЗКОВОЛЬТНЫХ СЕТЕЙ
3.1. Математическая модель электрической сети здания с учетом параметров ее основных элементов и характерных электроприемников
Во второй главе рассмотрены математические модели низковольтных сетей с нелинейными нагрузками, которые позволяют определить искажения синусоидальности кривых токов и напряжений в зависимости от доли нелинейной нагрузки и параметров моделируемых нелинейных потребителей для сетей НН различного исполнения. Данные модели можно использовать для анализа электромагнитных процессов в автономных и распределительных сетях НН при условии, что нагрузка сосредоточена в одном узле. При этом для городских распределительных сетей такой нагрузкой является эквивалентная нагрузка всех электроприемников крупного объекта (здания, предприятия). Очевидно, что с помощью рассмотренных моделей нельзя определить значение высших гармоник токов и напряжений внутренней электрической сети объекта и, соответственно, искажения синусоидальности их кривых на зажимах подключенных к ней электроприемников. Поэтому данные модели необходимо усовершенствовать путем дополнительного учета параметров элементов внутренней сети здания и определения характерных нагрузочных узлов подключения отдельных групп электроприемников.
Как правило, основными элементами электрической сети жилого или общественного здания являются трансформатор 10/0,4 кВ, внешние питающие линии от шин НН трансформатора к главному распределительному щиту (ГРЩ) здания, внутренние питающие линии (стояки) от ГРЩ здания к распределительным щиткам (РЩ), линии от РЩ силовой сети к силовым электроприемникам (распределительная сеть), линии от РЩ осветительной сети к светильникам и/или розеткам (групповая сеть).
Очевидно, что усовершенствованная схема замещения сети НН станет более сложной из-за дополнительного учета не только указанных элементов сети, но и соответствующих групп электроприемников, которые подключаются к ГРЩ, РЩ и розеткам.
Иными словами, в схеме замещения станет больше ветвей и узлов. При этом количество нагрузочных узлов будет определяться назначением здания, его размерами, этажностью, количеством помещений и составом электроприемников, и, в соответствии с этим, схемой сети (магистральная, радиальная, смешанная), количеством стояков, РЩ и розеток.
Понятно, что при учете всех узлов схема замещения сети будет чрезмерно сложной. Поэтому необходимо ее упростить путем эквивалентирования нагрузок в целях получения оптимального количества нагрузочных узлов, к которым подключаются характерные группы электроприемников с их конкретными параметрами. В результате указанного эквивалентирования в схеме замещения должны быть представлены основные элементы сети, а суммарная мощность ее электроприемников, напряжение в эквивалентируемых узлах и токи в примыкающих к ним сетевых элементах не должны существенно измениться.
Очевидно, что эквивалентирование нелинейных нагрузок будет иметь свои особенности. Суть их состоит в том, что в зависимости от поставленной задачи относительно определения параметров несинусоидальности тока и напряжения в каком-либо узле эквивалентная схема замещения сети должна включать в себя фрагменты сетевых элементов (участки линий), которые формируют путь протекания тока нагрузки этого узла. При этом в схеме замещения сети всегда должны быть представлены узел ГРЩ (в различных вариантах при эквивалентировании нагрузок изменяться будет только мощность присоединяемых к ГРЩ электроприемников), а также узел соседнего сетевого элемента, ближайший к рассматриваемому, и участок линии между ними. Например, при построении эквивалентной схемы замещения для определения токов и напряжений в узле групповой (распределительной) сети следует учесть, кроме внешней питающей сети и ГРЩ, участок (участки) стояка и участок (участки) линии групповой (распределительной) сети с соответствующим количеством их узлов.
На основании изложенного выше можно сформулировать основные положения метода эквивалентирования нелинейных нагрузок и построения эквивалентных схем замещения сети.
- Суммарная мощность электроприемников, подключенных к нагрузочным узлам схемы замещения сети, после эквивалентирования не должна измениться.
- Схема замещения сети строится по принципу формирования пути протекания тока рассматриваемой нагрузки. При этом в общем случае, в схеме замещения должны быть представлены все основные элементы сети: внешняя питающая сеть, участок (участки) стояка и участок (участки) линии групповой (распределительной) сети с соответствующим количеством нагрузочных узлов.
- В пределах каждого элемента сети выделяется один эквивалентируемый узел, к которому подключается дополнительная нагрузка других узлов этого элемента. В этих эквивалентируемых узлах его собственная нагрузка суммируется с нагрузкой электроприемников, подключенных вне пути протекания тока рассматриваемого нагрузочного узла, а именно:
а) в узле ГРЩ суммируется нагрузка всех стояков, кроме рассматриваемого;
б) в узле РЩ суммируется нагрузка соответствующих РЩ, а также всех линий групповой (распределительной) сети данного РЩ, кроме рассматриваемой;
в) в узле групповой (распределительной) сети суммируется нагрузка соответствующих электроприемников данной линии, кроме рассматриваемой группы электроприемников.
- При эквивалентировании нагрузок в узлах исключаются продольные сопротивления соответствующих сетевых фрагментов, расположенных вне пути протекания тока рассматриваемого узла, а эквивалентная нагрузка представляется активными и реактивными элементами, значение которых определяется ее суммарной мощностью.
Проведенный анализ показал, что, с учетом сказанного, оптимальной для проведения моделирования и анализа режимов электрической сети здания с несимметричными нелинейными электроприемниками будет схема замещения, которая учитывает четыре характерных нагрузочных узла (ГРЩ, РЩ и два узла (розетки) групповой сети).
Поэтому в работе [38] был рассмотрен вариант развернутой схемы замещения сети НН, который приведен на рис. 3.1.

Рис. 3.1. Развернутая схема замещения сети НН
Из развернутой схемы замещения видно, что внешняя питающая сеть и стояки выполняются трехфазными с нулевым проводом (сопротивления Ζ и Z8), а нагрузка групповой сети (НЗ, Н4) подключается к РЩ двужильным (фаза—нуль) проводом. Следует отметить, что нагрузочные блоки HI—Н4 идентичны по своему составу и подобны нагрузке рассмотренной выше упрощенной модели сети НН. Каждый нагрузочный блок состоит из трех однофазных нагрузок, включенных на фазные напряжения (рис.2.5). Изменяя соответствующие сопротивления, можно изменять как мощность, так и соотношения линейной и нелинейной составляющих этих нагрузок.
Нетрудно видеть, что развернутую схему замещения сети можно условно разделить на четыре подобные подсхемы, каждую из которых можно описать подобной системой дифференциальных уравнений. Для простоты рассмотрим дифференциальные уравнения, которые описывают одну подсхему замещения, в состав которой входят еa, ев, ес — система ЭДС; Z, Z2, Z3, Z4 — продольные линейные сопротивления сети и элементы нагрузки Н1. При этом можно выделить три группы уравнений. Первая группа уравнений описывает токи и напряжения линейной части подсхемы замещения и имеет следующий вид:

где I1-I8 — мгновенные значения токов в соответствующих сопротивлениях подсхемы замещения токов нагрузки. Очевидно, что для третьей и четвертой подсхем замещения уравнения будут более простыми из-за отсутствия токов нулевого провода.
Вторая группа уравнений описывает токи и напряжения нагрузочной части подсхемы замещения и имеет следующий вид:

где![]() — мгновенные значения фазных токов линейной части нагрузки HI;
— мгновенные значения фазных токов линейной части нагрузки HI;![]() — мгновенные значения фазных токов нелинейной (выпрямительной) части нагрузки HI; R"1-R"2.
— мгновенные значения фазных токов нелинейной (выпрямительной) части нагрузки HI; R"1-R"2.
Третья группа уравнений описывает фазные токи выпрямительной части нагрузки. Уравнения для определения тока однофазного выпрямителя нагрузки Н1 имеет следующий вид:
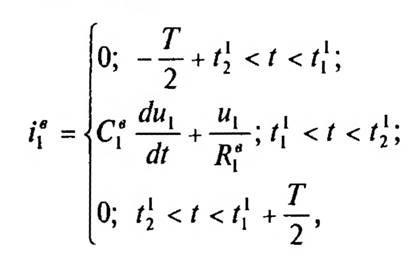
где С"1,R1 — емкость фильтра и активное сопротивление нагрузки однофазного выпрямителя; t1,t2 — моменты времени изменения состояния (отпирание-запирание) диодов указанного выпрямителя; Т — период. При этом момент времени определяется из условия равенства нулю тока, потребляемого выпрямителем рассматриваемой фазы:

Момент времени определяется из условия равенства напряжения и напряжения на нагрузке выпрямителя R“, поддерживаемого за счет запаса энергии в емкости С, которая была заряжена в предыдущий полупериод:
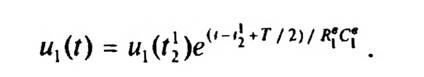
Аналогично записываются уравнения для остальных трех подсхем развернутой схемы замещения. Решив представленные дифференциальные уравнения, получим значения всех токов и напряжений моделируемой сети НН.
Таким образом, разработанная модель низковольтной сети с нелинейными нагрузками позволяет, в отличие от известных, определить значения искажений синусоидальности кривых токов и напряжений на зажимах электроприемников, подключенных в любой точке моделируемой сети НН. Результаты расчетов позволяют оценить и сопоставить уровень высших гармоник токов и напряжений на любом предусмотренном схемой замещения элементе сети в различных вариантах ее исполнения и состава электроприемников.

