Построение кривой провисания провода и определение стрел провисания
Общие сведения. Допускаемые напряжения в проводе
Жесткость проводов и тросов сказывается только при подвеске коротких отрезков проводов, например, длиной в несколько метров между гирляндами анкерных опор. При длине пролётов, принимаемых на воздушных линиях электропередачи, жесткостью проводов можно пренебречь и рассматривать их как идеальные гибкие нити, подвешенные в двух точках и подвергающихся воздействию равномерно распределенной нагрузки от собственного веса провода. Такая гибкая нить примет очертание цепной линии, как показано на рис. 2.11 [3, 11, 13].
Рис. 2.11. Кривая провисания провода при одинаковой высоте точек подвеса.
Согласно обозначениям на рис. 2.11, расстояние по горизонтали между точками подвеса А и В называется пролётом и обозначается буквой l. Расстояние по вертикали в середине пролёта между проводами и прямой АВ, соединяющей точки подвеса, называется стрелой провисания провода и обозначается буквой f. Обе величины измеряются в метрах. Сила, действующая в любой точке провода и направленная по касательной к кривой провисания, называется тяжением и обозначается буквой Т. Тяжение в низшей точке кривой провисания, направленное горизонтально, принято обозначать буквой Н. Оба вида тяжения измеряют в деканьютонах (даН) или килограмм - силах (кгс).
Сила, действующая на единицу сечения провода, называется напряжением, обозначается буквой σ и определяется по формуле:
(2.10)
даН/ мм , кгс/ мм ,
где T - тяжение в проводе, кгс (даН);
f - поперечное сечение провода, мм .
Согласно [13], механический расчет проводов и тросов производится по методу допускаемых напряжений, согласно которому необходимым условием является работа провода в пределах упругости его материала, то есть напряжения σ, возникающие в проводах или тросах при
воздействии наибольшей нагрузки или наинизшей температуры, должны быть меньше предела прочности материала проводника.
Допускаемое максимальное напряжение в проводе или тросе (даН/мм ) определяется в зависимости от временного сопротивления материала провода σΒ (даН/мм ) и принятого коэффициента запаса прочности n по формуле:
(2.11)
В [13] допускаемые напряжения установлены для трех исходных условий: 1) при наибольшей нагрузке; 2) при наинизшей температуре; 3) при среднегодовой температуре. При этом значения допускаемых напряжений при наибольшей нагрузке и наинизшей температуре имеют одинаковые численные значения [13, стр. 324, 325, табл. 2.5.7].
Определение стрелы провисания провода
Определение стрелы провисания провода при длине пролётов менее 800 метров
Если длина пролёта воздушной линии электропередачи составляет менее 800 м, расчет стрелы провисания провода производят по уравнению параболы [3, 11].
Для вывода уравнения кривой провисания провода примем систему координат с началом в низшей точке кривой провисания О, осью абсцисс X и осью ординат Y, как показано на рис. 2.12.
При выводе используются основные уравнения статики для системы, находящейся в равновесии:
а) сумма проекций всех внешних сил на координатные оси равна нулю:
Σ X = 0; Σ y = 0; (2.12)
б) сумма моментов всех внешних сил или их проекций относительно любой точки равна нулю:
Σ м = 0. (2.13)
Рассмотрим часть провода, разрезав его в низшей точке О и в любой точке D с координатами (х;у). Отрезанные части провода заменим соответствующими тяжениями: в низшей точке кривой провисания тяжением Н, а в точке D тяжением Т.
Так как для воздушных линий касательная к кривой провисания в любой точке имеет малый угол с горизонтальной прямой, то вес рассматриваемого участка можно принять равномерно распределенным по горизонтали и заменить сосредоточенной силой рх, действующей в
середине рассматриваемого участка, то есть на расстоянии х/2 от точек О и D, а силу тяжения Тх приравнивают к силе тяжения в наинизшей точке Н.
Направление действия силы Н в точке D противоположно по отношению к направлению этой же силы в наинизшей точке кривой провисания провода, так как вследствие свойств идеальной гибкой нити она может работать только на растяжение.
В этом случае уравнение моментов сил относительно точки D запишется следующим образом:
(2.14)
Решив уравнение (2.14) относительно у, получим основное уравнение кривой провисания провода:
2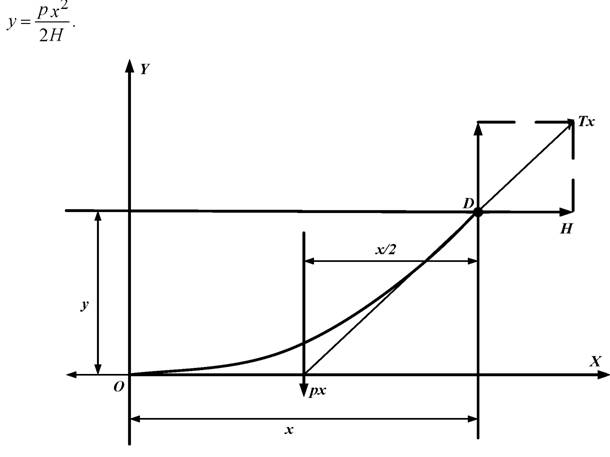
(2.15)
Рис. 2.12. Внешние силы, действующие на отрезок провода
В формулу (2.15) входят: единичная нагрузка на провод p и тяжение в низшей точке кривой провисания H. В практических же расчетах пользуются не тяжением, а напряжением в проводе σ, и не единичной нагрузкой, а удельной γ. Подставляя в формулу (2.15) p = γF и H = gF , получим:
(2.16)
Определение стрелы провисания провода при одинаковой высоте точек подвеса
Для определения стрелы провеса при одинаковой высоте точек подвеса достаточно подставить в формулу (2.16) значение x = I/ 2, тогда
(2.17)
Определение стрелы провисания провода при разной высоте точек подвеса
При разной высоте точек подвеса кривая провисания провода будет несимметричной и низшая точка кривой провисания провода будет находиться не в середине пролёта, а ближе либо к точке А, как показано на рис. 2.13, либо к точке В [3, 11].
В этом случае необходимо определять три различные стрелы провисания:
- fc - стрела провисания в середине пролёта, находится по выражению, тождественному выражению для стрелы провисания при одинаковой высоте точек подвеса провода, формула (2.17);
- fa - стрела провисания провода, измеряемая относительно ординаты низшей точки подвеса А, находится по формуле:
(2.18)
- fb - стрела провеса провода, измеряемая относительно ординаты высшей точки подвеса В, находится по формуле:
(2.19)
Рис. 2.13. Кривая провисания провода с разной высотой точек
подвеса
Определение стрелы провисания провода при длине пролётов более чем 800 метров
При длинах пролётов более чем 800 м погрешность значения стрелы провисания, определяемой по формуле (2.16), превышает допускаемую. В этом случае пользуются формулой, выведенной не из уравнения параболы, а из уравнения цепной линии, и определяют стрелу провисания по двучленной формуле:
(2.20)
Решение о том, допустимо ли пренебречь вторым членом формулы (2.20) или нет, делается на основании вычислений стрелы провисания. Если численное значение второго члена формулы (2.20) будет меньше чем 0,1% от значения стрелы провисания, то только в этом случае им можно пренебречь.
Пример 2.2
Пользуясь результатами примера 2.1, определить стрелу провисания провода АС - 240/32 нормальной конструкции для среднегодовых эксплуатационных условий работы. Провод будет смонтирован на унифицированных двухцепных свободностоящих стальных опорах 220 кВ.
Исходные данные и пояснения
Согласно техническим данным (табл. 2.1), провод АС-240/32 нормальной конструкции имеет поперечное сечение алюминиевого проводника Fс = 238 мм , а стального сердечника - Fc = 43,1 мм . Отношение площадей поперечных сечений алюминия и стали, обозначаемое ,
. В соответствии с [13, стр. 324, 325, табл. 2.5.7]
для сталеалюминиевых проводов сечением 120 мм2 и более при m = 6,11-6,25 допускаемое напряжение при среднегодовой температуре σд = 8,7 даН/мм . Среднеэксплуатационные условия работы провода характеризуются нагрузкой на провод γ1 = 0,35 · 10-2 даН/м мм2.
По условию задачи провод будет смонтирован на унифицированных двухцепных свободностоящих стальных опорах 220 кВ. Марка опоры П220-2 [6, стр. 40, табл. 1.34]. Для данного типа опор допустимыми являются промежуточные пролёты в пределах l = 470-345 м. Для решения примера примем 470 м.
Решение
Так как длина промежуточного пролёта менее чем 800 м, то стрелу провисания провода определим по формуле 2.17, тогда
Определение стрелы провисания провода при пересечении воздушными линиями электропередачи водных преград и инженерных сооружений
При проектировании воздушных линий требуется определять расстояние по вертикали от провода до различных пересекаемых инженерных сооружений или водных преград, чтобы проверить, будет ли соблюдаться допустимый габарит от низшей точки кривой провисания провода до сооружения или преграды [3, 11, 13, 14]. Как правило, в этих случаях бывает известна только высота точек подвеса провода на опорах (точки А и В), а высота низшей точки кривой провисания провода О не известна. Так как местонахождение точки О, которая одновременно является началом координат не известно, то принимают систему координат с началом в фиксированной точке, например, в одной из точек подвеса, которая расположена выше (точка А на рис. 2.14). Ось X направляют в сторону пролёта, а ось Y - вниз, параллельно действию нагрузки, как это показано на рис. 2.14.
Так как высоты точек подвеса А и В различны, а местонахождение точки О неизвестно, то условие статического равновесия нарушено. В этом случае помимо тяжения H необходимо учесть вертикальную реакцию V, параллельную оси Y, но противоположную ей по направлению.
Независимо от разницы в высотах точек подвеса провода вертикальная реакция зависит только от веса провода, равномерно распределенного по всей его длине, и равна весу, умноженному на половину длины пролёта:
(2.21)
Рис.2.14. К определению координат любой точки провода относительно начала, принятого в верхней точке подвеса
Составим уравнение моментов всех внешних сил, приложенных е произвольной точке Х с координатами (х;у) ( на рис. 2.14 точка Х находится в середине пролёта) с учетом сосредоточенной силы от собственной массы провода рх, действующей в середине рассматриваемого участка:
(2.22)
Искомой величиной в уравнении (2.22) является fx. Решая его относительно искомой стрелы провисания, получим:
(2.23)
(2.24)
В случае, если точка В окажется выше точки А, необходимо за начало координат принять точку В и изменить направление оси Х, направив ее в сторону пролёта, тогда уравнение 2.24 сохранится без изменения.
