Расчетные условия. Нагрузки на провода и тросы
Выбор расчетных климатических условий для воздушных линий, сооружаемых на территории России, производится с использованием карт районирования территории по гололеду и ветру [13].
Провода и тросы, подвешенные на опорах воздушных линий электропередачи, находятся под постоянным действием равномерно распределенной по длине статической нагрузки от собственного веса. Кроме того, на них могут действовать дополнительные нагрузки - вертикальная от гололеда и горизонтальная от ветра.
Вертикальная нагрузка от веса гололеда обычно вызывает наибольшие усилия в проводах, действует не постоянно, а при неблагоприятных атмосферных условиях. Она может существовать длительное время, поэтому ее считают основной при расчете проводов. Распределение гололеда по проводу не бывает строго равномерным. Учесть неравномерность не представляется возможным, поэтому такую нагрузку считают равномерно распределенной по длине провода.
Горизонтальная нагрузка от ветра, так же, как и нагрузка от гололеда, вызывает большие усилия в проводе, поэтому учитывается в расчетах. Неравномерность скоростного напора по длине пролёта учитывается коэффициентом неравномерности α.
Равномерно распределенная нагрузка в килограммах, отнесенная к 1 м длины провода, называется единичной нагрузкой и выражается в кг/м [3, 11, 13].
Единичная нагрузка от собственного веса провода р1.
Для вычисления нагрузки р1 пользуются данными о массе (весе) провода из действующих стандартов или технических условий, где обычно указывается вес провода в килограммах на один километр [6, стр. 53-57, табл. 1.47-1.52 и стр. 60-63, табл. 1.58-1.63]. Для получения единичной нагрузки от собственного веса провода в килограммах на один метр следует массу или вес, указанный в стандарте, умножить на 10 , тогда единичная нагрузка от собственного веса провода может быть вычислена по формуле:
Р1 = M п ·10-3, кг/м (даН/м), (21)
где M п - масса (вес) провода, кг.
Единичная нагрузка от гололеда р2
Рассмотрим рис. 2.9.
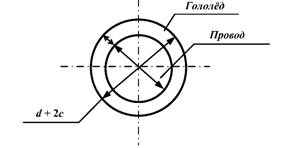
Рис. 2.9. Поперечное сечение расчетного приведенного гололеда
В соответствии с фигурой и обозначениями на рисунке, площадь сечения слоя приведенного гололеда F гол определиться по формуле:
![]() (2.2)
(2.2)
а вес на всей длине провода L - по формуле:
![]() (2.3)
(2.3)
где d п - диаметр провода, мм;
с - толщина стенки гололеда, мм;
L - длина провода, м;
g 0 - объемный вес, который при принятых выше единицах измерения dп, с, и L, равен g0 = 0,9 · 10 , кг/м мм (даН/м мм ).
С учетом формул 2.2 и 2.3 единичная нагрузка от гололеда может быть определена как:
![]() , кг/м (даН/м). (24)
, кг/м (даН/м). (24)
Результирующая единичная весовая нагрузка при гололеде p3
Полная вертикальная нагрузка при гололеде определяется как арифметическая сумма единичных нагрузок от собственного веса провода и веса гололеда:
Р3 = P1 + Р 2, кг/м (даН/м). (2.5)
Единичные нагрузки от давления ветра p4 и p5
При принятых выше обозначениях и при условии, что определяется только нагрузка от горизонтальной слагающей давления ветра, единичные ветровые нагрузки могут быть определены по формулам: (2.6) - при отсутствии гололеда и (2.7) - при гололеде на проводах:
![]() , кг/м (даН/м), (26)
, кг/м (даН/м), (26)
где α - коэффициент, учитывающий неравномерность скоростного напора ветра по пролёту воздушной линии [13, стр. 315, 316, пункт 2.5.30]; Cx - аэродинамический коэффициент;
Qн - скоростной напор ветра, даН/м [13, стр. 312, табл. 2.5.1].
Согласно [13], аэродинамический коэффициент принимается для проводов, свободных от гололеда, при dп ^ 20 мм - Cx = 1,1, а при dп < 20 мм - Cx = 1,2 . Для проводов любого диаметра, но покрытых гололедом, - Cx = 1,2 .
Учитывая, что при определении ветровых нагрузок на провода с гололедом, следует принимать значение скоростного напора 0,25Qн [13], получим
![]() , кг/м (даН/м).
, кг/м (даН/м).
Результирующие единичные нагрузки на провод без гололеда и с гололедом p 6 и p7
Совместное действие вертикальных и горизонтальных нагрузок на провода определяется как результирующие единичные нагрузки (примечание 2.1) по формулам: (2.8) - без гололеда и (2.9) - с гололедом (рис. 2.10).

Рис. 2.10. Совместное действие вертикальных и горизонтальных нагрузок на провод
(2.8)
(2.9)
Пример 2.1
Трасса сооружаемой воздушной линии электропередачи 220 кВ проходит по местности, относящейся к особому гололедному и IV ветровому районам. На унифицированных свободностоящих стальных опорах будут смонтированы провода марки АС-240/32 нормальной конструкции. Рассчитать единичные и удельные механические нагрузки на провода от внешних воздействий.
Исходные данные и пояснения
В соответствии с [6, стр. 54, табл. 1.48] провод АС-240/32 нормальной конструкции состоит из стального сердечника, свитого из 7 стальных проволок диаметром 2,8 мм и проводниковой части в виде 28 алюминиевых проволок диаметром 3,29 мм. Технические данные провода АС-240/32 приведены в табл. 2.1.
Примечание 2.1: следует заметить, что при механическом расчете проводов удобнее пользоваться не единичными, а удельными (приведенными) нагрузками, которые равны единичным, отнесенным к 1 мм2 поперечного сечения провода. Удельные нагрузки обозначают буквой γ и измеряют в кг/м мм2.
Технические данные провода АС-240/32
Таблица 2.1
Параметры | Проводник | Сердечник | Провод |
Сечение, мм2 | 238 | 43,1 | 281,1 |
Диаметр, мм | 21,6 | 8,4 | 30 |
Масса, кг/км | - | - | 997 |
Согласно [13], интенсивность внешних воздействий на конструктивные элементы воздушных линий 220 кВ принимают, исходя из частоты повторяемости наибольших гололедной и ветровой нагрузок 1 раз в 10 лет. При этом максимальный нормативный скоростной напор ветра на высоте до 15 м над поверхностью земли принимают в IV ветровом районе 65 даН/м [13, стр. 312, табл. 2.5.1], а нормативная толщина стенки гололеда для высоты 10 м над поверхностью земли в особом гололедном районе может составлять более 22 мм (для решения примера примем 22 мм) [13, стр. 317, табл. 2.5.3].
Решение
- Постоянно действующая нагрузка от собственной массы провода
По формуле (2.1) с учетом табл. 2.1 и примечания 2.1:

- Временно действующая нагрузка от массы гололедных отложений
по формуле (2.4)

- Суммарная вертикальная нагрузка от собственной массы провода и массы гололеда
по формуле (2.5)
- Горизонтальная нагрузка от давления ветра на провод, свободный от гололеда по формуле (2.6)

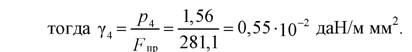
5. Временно действующая горизонтальная нагрузка от давления ветра на провод, покрытый гололедом по формуле (2.7)
6. Результирующая нагрузка от собственной массы и давления ветра по формуле (2.8)

7. Результирующая нагрузка от массы провода с гололедом и давления ветра
по формуле (2.9)
8. Вывод по примеру: сравнение нагрузок γ6 и γ7 показывает, что γ7> γ6, поэтому наибольшей нагрузкой является седьмая, то есть γ 7 = γ нб и в дальнейших расчетах следует ориентироваться на γ 7.
Примечание 2.2: примем направление ветра под углом 90°, тогда sin2ф<P = 1. Примечание 2.3: для данной нагрузки коэффициент неравномерности α определяется от значения 0,25Q н, например, для решаемой задачи
0,25<2н = 0,25 · 65 = 16,25 даН/м2, тогда α=1 [13, стр. 315, 316, пункт 2.5.30].

