3,4 Эквивалентная полоса частот, эквивалентное разрешение и центральная предельная теорема
Шаде [5] установил, что видимая резкость телевизионного изображения может быть в известной мере описана интегралом, взятым по всей области частот от квадрата МПФ телевизионной си-стемы.
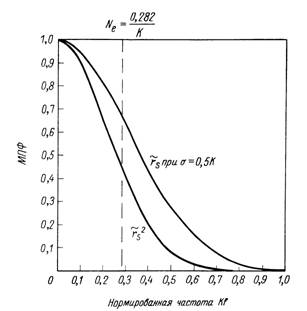
Фиг. 3.27. Пример эквивалентной полосы частот для МПФ гауссовой формы.
Шаде назвал этот интеграл эквивалентным числом линий Ne (по всей высоте кадра)
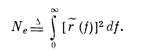(3.60)
Эта величина в действительности представляет эквивалентную полосу частот (фиг. 3.27). Величина Ne — один из лучших критериев оценки резкости и разрешения в частотной области для нешумящих изображающих систем. (Смысл и значение параметра Ne подробно разбираются в разд. 4.10.)
Если Ne является эффективной мерой разрешения в частотной области, то должен существовать соответствующий параметр и в пространственной области, который будем называть эквивалентным разрешением. Сенделл [42] рассмотрел различные возможные определения эквивалентного разрешения г и считает, что наилучшим является г — 1/2 Ne, поскольку это дает г = а для прямоугольной функции рассеяния. На фиг. 3.28 приведены Ne и г для некоторых распространенных ОПФ. Недостатком приведенного определения г является то, что г — не обязательно угловой размер наименьшей детали, разрешаемой системой.
Фиг. 3.28. Примеры значений эквивалентной полосы частот и эквивалентного разрешения.
Хорошо известная в теории вероятностей и статистике центральная предельная теорема имеет аналог [3] в теории линейной фильтрации: произведение п ограниченных по полосе непрерывных модуляционных передаточных функций (МПФ) стремится к гауссовой форме, когда п становится большим г). Многие системы тепловидения имеют как минимум четыре компоненты МПФ, а часто и семь, так что функция рассеяния линии для системы в целом часто может быть весьма точно аппроксимирована гауссоидой г (х) = ехр (— х* /2а2), где а — среднеквадратичное отклонение. Соответствующая МПФ равна
(3.61)
*Строгая формулировка центральной предельной теоремы дана в работе [43].
В качестве примера в табл. 3.5 и на фиг. 3.29 показаны компоненты МПФ, относящиеся к системе с разрешением порядка 1 мрад; МПФ системы в целом имеет приблизительно гауссову форму. Для целей анализа и описания имеет смысл отметить некоторые свойства этой функции. Среднеквадратичное отклонение функции рассеяния можно оценить, определив точки г (а) = 0,61 или г (1,175а) = 0,5. Масштаб МПФ можно найти, определив частоту / = 0,159/а, на которой г = 0,61. Различные оценки размера функции рассеяния для определенного процентного содержания полной энергии функции рассеяния Р в интервале значений между х = — х0 и х = х0 для гауссоиды можно сделать по следующим данным:
Другой путь аппроксимации МПФ гауссоидой — найти значение а, которое обеспечивает равенство гауссовой величины Ne = = 0,141/а фактической величине Ne функционально неизвестной
МПФ для примера конкретной системы
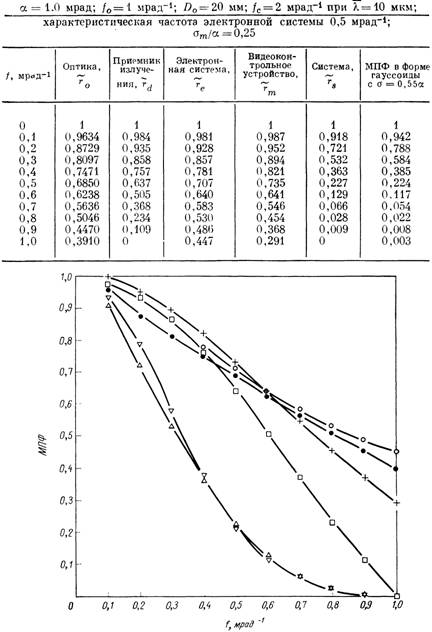
Фиг. 3.29. МПФ для примера системы.
# оптическая система; D приемник излучения; О электронная система; 4- видео- контрольное устройство; А система; у гауссоида.
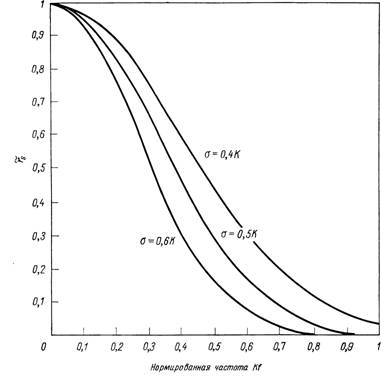
Фиг. 3.30. Примеры МПФ, имеющих форму гауссоид.
МПФ. На фиг. 3.30 показаны три универсальные гауссовы кривые в зависимости от безразмерного параметра Kf для величин а = = 0,4 К, 0,5 К и 0,6 К. Эти кривые можно использовать для определения влияния величины а на МПФ системы путем выбора значений К. К — 0,25 мрад дает систему с номинальным разрешением
- 25 мрад и с граничной частотой ~ 4 мрад-1; при этом кривые МПФ соответствуют величинам а = 0,1, 0,125 и 0,15 мрад.
ЛИТЕРАТУРА
- Гудмен Дж., Введение в фурье-оптику, изд-во «Мир», М., 1970.
- О’Нейл Э., Введение в статистическую оптику, изд-во «Мир», М .,1966.
- Bracewell R. N., The Fourier Transform and its Applications, McGraw- Hill, 1965.
- Duffieux P. М., L’integrale de Fourier et ses applications a l’Optique, Societe anonyme des imprimeries Oberthur, 1946.
- Schade О. H., Electro-Optical Characteristics of Television Systems,
