ГЛАВА ВТОРАЯ
СИСТЕМЫ СОСТАВЛЯЮЩИХ
Общие положения
При исследовании режимов работы электроэнергетических установок используются различные системы составляющих:
Система составляющих Обозначение
Симметричных (Фортескью) ............120
Кларка ....................................................αβΟ
Парка ...........................................dq 0
Трехфазная .............................................АВС
Использование систем составляющих 120, αβΟ и dqO представляет определенные преимущества при исследовании эксплуатационных и аварийных режимов трехфазных сетей, выполняемом на электродинамических моделях, а также при численных расчетах таких режимов на ЭЦВМ.
При этом стремятся заменить исходную цепь с трансформаторами, взаимными индуктивностями, емкостями и вращающимися машинами эквивалентными источниками напряжения (U), сопротивлениями (R), индуктивностями (L) и емкостями (С); если возможно, взаимные индуктивности (М) не применяют. Однако в общем случае, особенно при использовании трехфазной системы АВС для математического описания процессов, это удается не всегда. Вместе с тем раздельное математическое описание трехфазной цепи в виде независимых однофазных цепей оказывается возможным при использовании других систем составляющих; это приводит к ряду упрощений. В частности, взаимные индуктивности, емкости между элементами фаз трехфазной цепи могут быть выражены в виде эквивалентных индуктивностей или емкостей, соответствующих только каждой фазе. При этом число элементов, ветвей и узлов сокращается.
а. Трехфазная система (система составляющих АВС).
В симметричной трехфазной системе токи в фазах имеют одинаковое значение; то же справедливо и для фазных напряжений. Для описания такой трехфазной системы достаточно вычислить токи и напряжения только для одной фазы. Однако в аварийных режимах, например при однофазном или двухфазном коротком замыкании, имеет место несимметричная нагрузка. Кратковременно она также имеет место, например, при отключении от сети симметричной нагрузки, так как в этом случае выключатели в отдельных фазах одновременно не срабатывают. Для того чтобы исследовать такие процессы, во многих случаях сеть рассматривается как трехфазная.
При использовании трехфазной системы составляющих оказывается необходимым вводить в уравнения и в эквивалентные схемы емкости между фазами. Однако взаимные индуктивности могут быть пересчитаны и представлены в виде индуктивностей, если все электромагнитные устройства в сети работают циклически симметрично, т. е. форма тока (и напряжения) во всех трех фазах одинакова.
Так как в общем случае полное сопротивление прямой и нулевой последовательности у электромагнитных устройств в сети различны, то необходимо помимо трех проводов устанавливать в качестве четвертого провода также и обратный. Если при этом полное сопротивление нулевой последовательности меньше, чем прямой, как, например, это имеет место для трансформатора, то полное сопротивление четвертого провода должно быть принято отрицательным; для физических моделей это осуществить в широком диапазоне частоты затруднительно. Кроме того, отметим, что у линии переменного тока обратные токи в земле образуют с внешними проводами малые контуры и тем самым следуют вдоль линии. Использование системы АВС при моделировании сложной разветвленной трехфазной сети требует применения специальных преобразователей (рис. 1). При этом их необходимо установить так, чтобы они были включены во все замкнутые контуры. У мощных сетей это требование приводит к дополнительным трудностям, так что для моделирования оказывается целесообразным использование других систем составляющих. Определенные недостатки системы АВС проявляются и при расчетах на аналоговых устройствах, особенно если число элементов велико.
Особые трудности применение системы АВС вызывает в случае, если у электрической машины (генератора или двигателя) полное сопротивление прямой и обратной последовательности различно, причем это обстоятельство обязательно должно быть учтено, например, при расчете токов несимметричных коротких замыканий. Решение оказывается возможным, если включить дополнительное напряжение в систему обратной последовательности, т. е. образовать несимметричную звезду напряжений.
Таким образом, система АВС имеет определенные преимущества и недостатки, как и любая другая система составляющих. Хотя она и наглядна, но часто не позволяет дать достаточно точное описание процессов в цепи.

б. Система симметричных составляющих (система составляющих 120).
Исследование электрических машин с учетом не одинаковых полных сопротивлений прямой и обратной последовательности возможно при использовании системы симметричных составляющих. Эта система предусматривает разложение несимметричной трехфазной системы на три симметричные: прямой последовательности, обратной последовательности и нулевой последовательности, причем эти три системы не являются магнитосвязанными. Недостатком системы симметричных составляющих является наличие комплексных операторов, которые содержатся в уравнениях, используемых при переходе от заданной системы к системам прямой, обратной и нулевой последовательности. При моделировании это требует использования комплексных преобразователей. Такие преобразователи для широкого диапазона частот могут быть выполнены лишь электронными. Поэтому система симметричных составляющих используется преимущественно для исследования установившихся режимов.
в. Система составляющих αβ0 (система составляющих Кларка).
Эта система особенно удобна для исследования не установившихся режимов. В уравнениях для перехода от системы АВС к системе αβ0 содержатся лишь вещественные и постоянные коэффициенты. Однако использование этой системы для моделирования процессов в электрических машинах возможно лишь в случаях, когда полные сопротивления прямой и обратной последовательности можно принять равными, а также если равны сопротивления по продольной и поперечной осям (см. главу 5). Это предположение может оказаться во многих случаях справедливым для неустановившихся процессов высокой частоты.
г. Система составляющих dq0 (система составляющих Парка).
Эта система наиболее соответствует особенностям конструкции электрических машин. Она позволяет учесть неравенство эквивалентных сопротивлений контуров электрической машины по продольной и поперечной осям. Однако система составляющих достаточно сложна; при переходе от системы АВС к системе dq0 требуется выполнить весьма сложные преобразования.
Системы составляющих, указанные на стр. 24, предполагают, что уравнения, которые описывают исследуемые процессы, линейны. Только в этом случае исходную систему можно подразделить на несколько составляющих, которые не являются магнитосвязанными. Однако, если требуется учесть насыщение активной стали, то при использовании, например, системы dq0 оказывается необходимым ввести дополнительную индуктивную связь между отдельными составляющими с учетом нелинейной характеристики магнитной цепи машины. Отметим, что некоторые типы устройств с нелинейными характеристиками, например, удобно исследовать с помощью системы AВС .
д. Выбор системы составляющих.
Переход от одной системы к другой. Для трехфазной сети, в которой форма кривой тока (и напряжения) во всех фазах одинакова, может быть в общем случае использована система симметричных составляющих или же система αβ0. Таким образом трехфазная сеть может быть преобразована к нескольким однофазным, максимальное число которых равно трем. Если требуется исследовать несимметричные режимы, например однофазное короткое замыкание или разрыв в фазе, то тогда необходимо использовать прямую, обратную и нулевую системы, причем для электрических машин следует учесть соответствующие полные сопротивления для каждой системы. Если же требуется исследовать неустановившиеся процессы, целесообразно применить систему составляющих αβ0. В случае простейших аварийных режимов, если полные сопротивления прямой и обратной последовательности равны, достаточно, как правило, использовать прямую и нулевую системы либо систему а и нулевую, причем эквивалентные схемы аналогичны.
В аварийных режимах, несимметричных относительно какой-либо фазы, например фазы Л, использовать систему симметричных составляющих для моделирования сложнее, чем систему составляющих αβΟ, так как в схему необходимо ввести комплексные преобразователи. Поэтому целесообразно исследовать раздельно аварийный режим в одной фазе (A) и замыкание между двумя фазами (В и С). Однако для многих аварийных или несимметричных режимов, возникающих одновременно, это не всегда возможно.
В периодической литературе приведены схемы замещения для различных аварийных режимов (однофазное короткое замыкание, разрыв в фазе и др.). Эти схемы замещения не могут быть использованы, если аварийные ситуации следуют сразу друг за другом, что часто имеет место на практике. Предположим, например, что нам необходимо исследовать процессы при отключении трехфазного короткого замыкания. Тогда мы имеем последовательность режимов:
трехфазное короткое замыкание в фазах A, B, С;
разрыв в фазе Л (дуга в выключателе фазы Л разрывается в первую очередь);
разрыв в фазах А и В (дуга в выключателе фазы В разрывается во вторую очередь);
разрыв в фазах A, В, С (дуга в выключателе фазы С разрывается в последнюю очередь).
Как правило, на модели нельзя осуществить переключение с одной схемы замещения на другую столь быстро, чтобы получить соответствующий непрерывный процесс с учетом работы выключателей в фазах. Это связано с тем, что неустановившийся процесс, вызванный разрывом дуги в выключателях отдельных фаз, таким путем учесть не удается. Поэтому ниже приведены общие схемы замещения, которые обеспечивают переход от одной системы составляющих к другой вне зависимости от вида аварийного режима. Далее оказывается возможным для одной и той же цепи, состоящей, например, из линии передачи и ряда электрических машин, описать процессы в линии в системе αβ0, а в машинах — в системе 120; соответственно этому можно выполнить модель такой цепи, подключить на зажимы A, В или С несимметричную нагрузку, а также измерить на модели напряжения между точками A, B, С и нулевой точкой (нейтралью) либо измерить токи в фазах.
Введение дополнительной индуктивной связи позволяет лишь приближенно учесть взаимное влияние, так как сама величина этой связи, а также формы кривых исследуемых величин являются сложными функциями интенсивности процессов. (Прим. редактора перевода.)
Соотношения для перехода от одной системы составляющих к другой

Рис. 3
а. Схема перехода. Как отмечалось выше, одна и та же цепь может быть описана частично в системе αβ0, а частично— в системе 120 либо dq0. Однако почти всегда при выполнении модели в той или иной системе составляющих необходимо зажимы А, В, С и нулевой сделать доступными, чтобы можно было измерить определенные величины или же воспроизвести аварийные режимы.
При исследовании процессов должны быть известны общие соотношения для перехода от одной системы составляющих к другой.
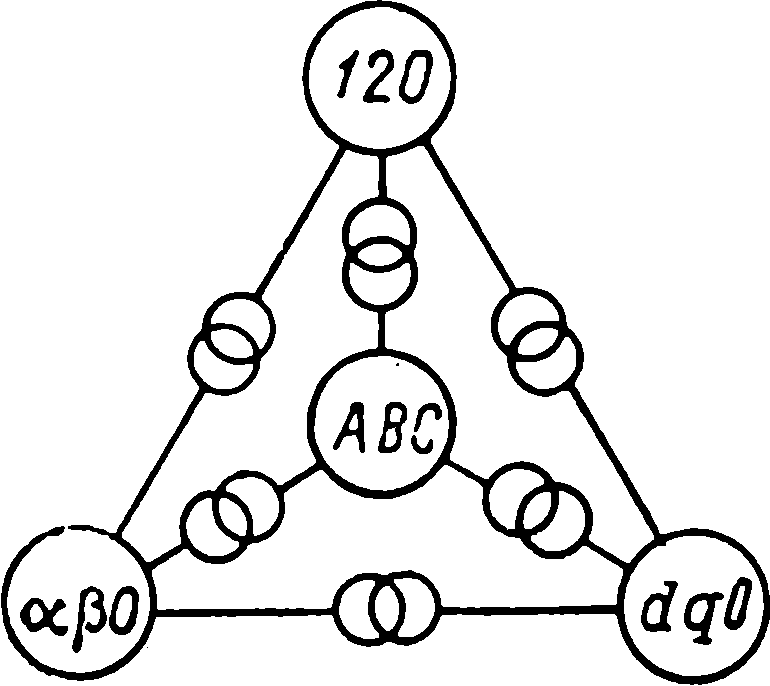
Рис. 2
На рис. 2 представлена схема возможных переходов (преобразований). Большими кружками обозначены указанные выше четыре системы составляющих, а символами, которыми на электрических схемах обозначаются трансформаторы,— соотношения для перехода от одной системы к другой и соответствующие им эквивалентные схемы.

б. Принцип построения системы составляющих. Каждая система составляющих выполняет преобразование трех заданных величин в три другие, причем при преобразовании необходимо выполнить определенные условия. Предположим, например, что три напряжения иа, ub, ис необходимо преобразовать в напряжение и1, и2, и3. В общем случае можно записать или в матричной форме
Эквивалентная схема, которая соответствует этой системе уравнений, содержит девять преобразователей (рис. 3). Используя эту схему, нетрудно записать выражения для токов:
 (3)
(3)
или в матричной форме
![]() (4)
(4)
В такой схеме имеются две связанные между собою цепи, из которых для одной использована система составляющих abc, а для другой — система составляющих 123.
Подводимая мощность, выраженная в комплексной форме через токи и напряжения одной системы, равна отводимой мощности, выраженной через токи и напряжения другой. В этом случае говорят об инвариантности выражения комплексной мощности. Этот вопрос рассмотрен в п. «в».
Однако для применения различных систем составляющих ознакомление с ними не обязательно.
в. Инвариантность выражения комплексной мощности. Из условия инвариантности выражения для мощности в комплексной форме следует
![]() (5)
(5)
Токи и напряжения должны быть преобразованы в соответствии с одними и теми же матричными выражениями. Поэтому с учетом уравнений (2) и (4) получаем
![]() (6)
(6)
Отсюда для матрицы преобразования Т можно вывести следующие условия:
![]() (7)
(7)
Здесь Е — единичная матрица.
Полученные таким путем составляющие называются нормированными.

