Разработка математической модели трансформатора для использования методов математического программирования
Выше указывалось, что использование математического аппарата некоторых методов математического программирования обусловлено определенными требованиями как к виду исследуемой математической модели, состоящей из системы нелинейных уравнений или функциональных зависимостей, так и к характеру изменения функциональных аргументов. В частности, функции должны быть дифференцируемыми и, естественно, непрерывными; варьируемые параметры не должны изменяться дискретно, связь лимитирующих технических параметров с варьируемыми переменными должна быть выражена в виде равенств.
Несмотря на определенные ограничения к использованию этих методов, преимущества, которые они представляют исследователю (направленность и малое время поиска, широкий диапазон исследования), в ряде случае оправдывают допущения, к которым приходится прибегать при составлении математической модели исследуемого объекта.
Одним из основных требований промышленного проектирования трансформаторов является учет дискретного характера изменения основных конструктивных элементов в процессе оптимизации (диаметра стержня магнитопровода, числа витков, числа слоев, размеров обмоточного провода и др.).
Вместе с тем учет дискретности всех конструктивных элементов при составлении математической модели и исследовании ее с помощью методов математического программирования не всегда оказывается возможным. В ряде случаев, когда эти методы применяются, например, при предварительных расчетах и поиске оптимальной зоны, при исследовании влияния отдельных параметров на характеристики трансформатора, при исследовании обобщенных характеристик трансформатора и т. д., дискретно изменяющиеся переменные могут быть заменены непрерывными. Наиболее обоснованно это можно делать там, где дискретность слабо выражена. Такая замена, в частности, возможна в отношении числа витков в обмотках трансформаторов малой и средней мощности, где оно обычно большое, и округление полученного после расчета на ЭВМ дробного числа витков до целого не приводит
к изменению результатов расчета. Эта замена возможна также в отношении размеров обмоточного провода, например, когда требуемая точность расчетов не обеспечивается размерами обмоточного провода из-за дискретности сортамента.
В случае замены дискретно изменяющихся переменных непрерывными полученные в результате расчета оптимальные значения переменных должны затем уточняться в соответствии с заданными условиями на проектирование: например, размеры обмоточных проводов должны заменяться ближайшими значениями из дискретного ряда, количества витков в обмотках должны округляться до целого витка и т. д. Расчетные характеристики и параметры трансформаторов, в этом случае должны быть также уточнены с учетом этой замены. Учет дискретности переменных наиболее целесообразно выполнить при детальном расчете трансформатора, принимая значения переменных из дискретного ряда в пределах найденной оптимальной зоны.
При таком подходе к поиску оптимального решения выполнение окончательных расчетов по дискретным значениям варьируемых переменных на основе найденных оптимальных зон по затратам машинного времени может быть уменьшено во много раз и осуществлено на заключительном этапе расчета.
Однако подобная замена дискретных величин на непрерывные не всегда оправданна. Это нецелесообразно делать в отношении геометрических размеров, дискретный характер изменения которых явно выражен, а отклонение которых: от заданных дискретных значений приводит к заметным изменениям параметров и характеристик трансформатора.
Замена лимитирующих неравенств уравнениями оказывается невозможной в тех случаях, когда технические параметры или характеристики задаются в узких пределах и не являются функцией других оптимизируемых величин. Это, например, относится к такому лимитеру, как напряжение КЗ, значение которого регламентируется стандартом. Для трансформаторов, у которых плотность тока в обмотках или магнитного потока в стержне магнитопровода определяется только техническими соображениями (температурой обмоток, значением тока XX) и не выбирается с учетом экономических соображений, эти лимитеры могут быть также представлены в виде уравнений. Это, в частности, имеет место при использовании в качестве оптимизируемого технико-экономического критерия минимальной стоимости, массы или объема трансформатора. Чаще всего это может быть при проектировании трансформаторов малой и средней мощности, а также при проектировании трансформаторов для специальных условий.
Рассмотрим в качестве конкретного примера математическую модель сухих трехфазных трансформаторов с эпоксидной изоляцией обмоток, имеющих стержневой магнитопровод, цилиндрические слоевые обмотки первичного напряжения НН и секционные обмотки вторичного напряжения ВН. Обмотки залиты эпоксидным компаундом. Серия трансформаторов охватывает диапазон мощностей 1,6—63 кВ·А с напряжением обмотки ВН до 22 кВ. Трансформаторы предназначены для длительной работы при естественном воздушном охлаждении [76].
В качестве лимитирующих технических условий приняты: превышение температуры обмоток над температурой воздуха, значения тока XX и напряжения КЗ трансформатора. В качестве критерия экономичности могут быть приняты в зависимости от конкретных условий объем трансформатора, масса активных материалов или стоимость трансформатора.
В качестве варьируемых параметров, в полной мере определяющих геометрию и характеристики трансформатора, приняты: диаметр стержня магнитопровода dc, индукция в стержне магнитопровода Вс (или число витков в обмотке НН W1, число-слоев обмотки НН Ν1, число секций обмотки ВН пс, размеры обмоточных проводов. При составлении математической модели для рассматриваемой конструкции трансформатора принято, что размеры обмоточных проводов изменяются не дискретно, а непрерывно. Вместо дискретно изменяющихся Ν1 и пс приняты коэффициенты геометрии β, Κ1 и К2, использование которых в известной мере упрощает составление математической модели
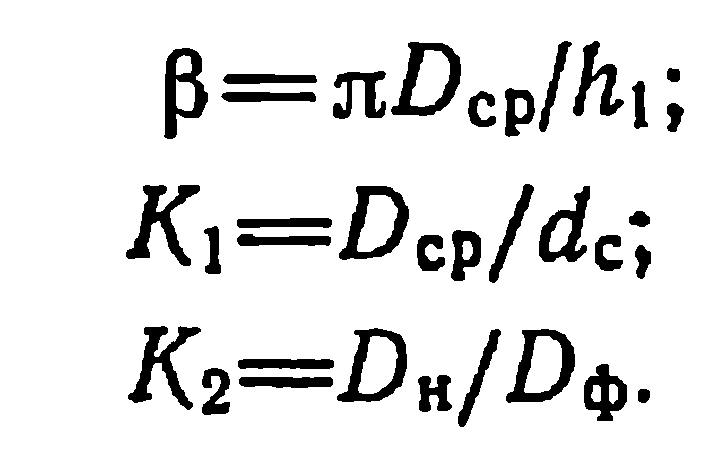
Отказ от учета дискретности размеров обмоточных проводов и замена дискретных переменных N1, пс, W1 коэффициентами β, К1, К2 и индукцией Вс могут быть допущены для трансформаторов рассматриваемой серии, поскольку дискретный ряд диаметров круглых обмоточных проводов приближается к непрерывному, а «цена» одного витка обмотки составляет менее 1%. Как будет показано далее, использование коэффициентов геометрии позволяет относительно просто составить математическую модель трансформатора, найти путем ее исследования оптимальный вариант и затем сделать реальную раскладку обмоток с учетом дискретности обмоточных проводов, числа слоев и секций в пределах полученных оптимальных геометрических размеров и характеристик трансформатора.
Разработка математической модели заключается в математическом описании связей между параметрами, характеристиками трансформатора и его конструктивными данными или, другими словами, в составлении проектных уравнений взаимосвязи номинальных параметров (мощности, напряжений и частоты , напряжения КЗ ик и т. д.) с принятыми варьируемыми параметрами.
К числу заданных параметров, в значительной степени влияющих на оптимальные соотношения основных геометрических размеров в трансформаторе, относится полное сопротивление обмоток трансформатора zтр или напряжение ик. Поэтому в качестве основного проектного уравнения взаимосвязи примем уравнение, устанавливающее математическую, зависимость между коэффициентами β, Κ1, К2, напряжением ик и номинальными параметрами трансформатора. Математическая модель трансформатора составлена также с учетом заданного превышения температуры обмоток над температурой воздуха Δτ.
Замена неравенств, ограничивающих заданные пределы изменения ик и ∆τ, равенствами допустима, так как значения ик и Δτ задаются в узких пределах, а выбор плотности тока в обмотках производится по заданной температуре обмоток.
Для трансформаторов средней и большой мощности, у которых реактивная составляющая напряжения КЗ икр является преобладающей, т. е. имеет место неравенство иКp>ика, зависимость между основными геометрическими размерами трансформатора и uкр. выражается уравнением вида![]()
где Aк — коэффициент, зависящий от номинальной мощности, трансформатора, реактивной составляющей напряжения КЗ, частоты питающей сети и др.; п — степенной коэффициент, равный 0,25—0,33.
Для трансформаторов рассматриваемого диапазона мощностей, условие Uкр^^Uка выполняется только для мощностей порядка. 40 кВ-А и выше; для трансформаторов меньших мощностей икa, оказывается соизмеримой с uKP, поэтому она также должна учитываться при выборе оптимальных геометрических соотношений.
В проектные уравнения, кроме номинальных данных трансформатора, входят величины, которые либо принимаются при проектировании однозначно (φст, αs, cos φтр и т. д.), либо выбираются в ходе расчета с учетом заданных характеристик (Вс, q).
Поиск оптимального варианта трансформатора может быть выполнен с помощью полученных проектных уравнений (4.55) для дискретно изменяющихся значений диаметра dc и индукции Вс при использовании итерационного процесса по коэффициенту геометрии К1.
Выбор вариантов трансформатора, удовлетворяющих заданным u и Δτ, с учетом реального конструктивного исполнения обмоток, может быть выполнен путем решения полученной системы нелинейных уравнений (4.57).
Система уравнений с переменными dc, β, К1, Κ2 может быть решена одним из методов вычислительной математики для нескольких заданных значений какой-либо из переменных, например диаметра dc, который для унифицированного ряда диаметров магнитопроводов изменяется дискретно. Полученные решения системы соответствуют технически приемлемым вариантам, удовлетворяющим заданным параметрам и характеристикам. Варианты, не удовлетворяющие этим условиям, из рассмотрения автоматически исключаются, что значительно сокращает время поиска оптимального варианта.
Из множества полученных технических решений должно быть выбрано одно, соответствующее наибольшему технико-экономическому эффекту. Для этого используется целевая функция, устанавливающая связь технико-экономического показателя трансформатора с принятыми варьируемыми переменными и основными номинальными параметрами трансформатора.
Полученная математическая модель трансформатора позволяет использовать для ее исследования, поиска наилучшего решения математический аппарат классических методов вычисления экстремумов функций и с минимальными затратами времени найти оптимальное решение.
Вместе с тем следует отметить, что математическая модель трансформатора, составленная применительно к конкретной конструкции магнитопровода и обмоток в виде системы нелинейных уравнений, не позволяет оперативно ее модифицировать при изменении конструкции трансформатора или расчетных формул. Кроме того, такая форма математического моделирования теряет наглядность или в некотором смысле «теряет физический смысл», так как отходит от установившихся инженерных методик расчета, что нельзя признать положительным фактором такого моделирования.

