При решении задачи оптимизации необходимо сформулировать ее в терминах математического программирования, а затем в соответствии с теорией оценить следующие аспекты: особенности построения математической модели; природу и число регулируемых параметров; вид допустимой области; характер целевой функции.
Выяснение этих вопросов дает возможность сначала установить класс задачи, а затем перейти к выбору методов ее решения. При этом количество рассматриваемых методов поиска оптимального решения значительно сокращается, так как часть этих методов не обеспечивает достижения результата, а другая часть оказывается труднореализуемой.
Процесс построения математической модели технической системы или объекта содержит следующие общие этапы: формализацию задач проектирования; анализ и выделение существенных свойств объекта; построение математического описания, отражающего взаимосвязь между собой выделенных свойств объекта.
Основной информацией для формализации задачи проектирования являются данные о назначении, условиях применения и режимах работы проектируемого объекта, а также о характере и целях проектирования. При этом задача записывается в виде (4.1) — (4.3). Учет особенностей проектируемого объекта заставляет вносить коррективы в постановку задачи.
Построение математической модели объекта осуществляется на базе фундаментальных законов, лежащих в принципе его функционирования. Так, в математической модели трансформатора основополагающим является закон электромагнитной индукции.
Поскольку любая модель лишь приближенно отражает свойства моделируемого объекта, важная задача разработчика модели заключается в нахождении компромисса между сложностью модели и точностью моделирования, которая, в свою очередь, должна согласовываться с точностью входной информации об объекте. Этот компромисс достигается за счет выделения существенных свойств объекта и отбрасывания второстепенных факторов, не влияющих на результаты проектирования. Здесь под свойствами понимаются величины, отражающие поведение реального объекта и учитывающие как технико-экономические показатели, так и условия функционирования; Варьируемые параметры являются независимыми свойствами. Другие r свойств зависят от варьируемых параметров и являются характеристиками объекта. Обозначим их вектором G=(g1, g2, gr).
Математическая модель объекта проектирования определяется следующими варьируемыми параметрами и характеристиками:
 (4.7)
(4.7)
В (4.7) входит также и выражение для целевой функции (4.3), являющейся оптимизируемой характеристикой объекта.
Таким образом, под математической моделью реального объекта будем понимать конечное множество варьируемых переменных {X} вместе с математическими связями (4.7) между ними и характеристиками G [66].
При ручном проектном расчете математическая модель объекта представляет последовательность расчетных формул, максимально упрощенных для ручного счета. Кроме этого, расчетчик пользуется многочисленными табличными и графическими зависимостями, а также ТИ, РТМ, ГОСТ. Задача проектирования заключается в определении параметров и характеристик реального исполнения, имеющего достаточно хорошие технико-экономические показатели. При этом речь идет не об оптимальном варианте, так как эвристические способности даже опытного проектировщика в лучшем случае позволяют получить результат, отличающийся от оптимального не менее чем на 5—10% [67].
Наметив цель получения оптимального варианта, мы тем самым значительно изменяем постановку задачи. Результат в этом случае должен удовлетворять следующим основным требованиям:
соответствовать общепромышленным нормам и иметь заданные технические характеристики;
быть наилучшим с точки зрения выбранного критерия эффективности.
Такой подход накладывает на организацию вычислительного процесса особые условия: во-первых, последовательность вычислений должна носить итерационный характер и базироваться на основе определенного метода поиска экстремума; во-вторых, большой объем вычислений обусловливает необходимость применения вычислительной техники, что предполагает полную формализацию математической модели объекта путем представления ее в виде вычислительного алгоритма.
Применение при оптимизационном проектировании вычислительной техники позволяет полнее удовлетворить требование адекватности математической модели и реального объекта в основном за счет усложнения зависимостей (4.7). При этом количество выполняемых операций не может превышать некоторое предельное значение в связи с тем, что: алгоритм должен размещаться в отведенной для него памяти ЭВМ; конечный результат должен быть получен в практически приемлемое время.
Опыт практической работы по разработке и отладке алгоритмов оптимизации силовых трансформаторов показывает, что наиболее определена и постоянна в этой задаче математическая модель трансформатора, а многочисленные изменения в формировании плана решения задачи и его реализации касаются вычислительного метода и мест «стыковки вычислительного метода с оптимизируемой моделью.
Особую роль в математической модели, как отмечалось выше, играют варьируемые параметры, под которыми будем понимать переменные, подвергающиеся изменению по определенному закону с целью нахождения такого их сочетания, которое обеспечивает наименьшее значение целевой функции (4.3) и удовлетворяет заданным ограничениям (4.1) и (4.2). В математической модели варьируемые параметры являются тем механизмом, при помощи которого осуществляется передача информации между целевой функцией, заданными ограничениями и характеристиками объекта [68].
Между задаваемыми исходными параметрами, характеристиками трансформатора и варьируемыми проектными параметрами существует подвижное соответствие: каждый варьируемый параметр может быть зафиксирован и введен в ЭВМ в составе исходных данных, с другой стороны, некоторые задаваемые параметры трансформатора можно подвергнуть варьированию с целью определения их оптимальных значений.
Поэтому целевая функция (4.3) может быть представлена в более общем виде
![]() (4.8)
(4.8)
где Xj — варьируемые проектные параметры, j= 1, 2, ..., п; yi— оптимизируемые неварьируемые параметры, /=1, 2, ..., k; Zf — неоптимизируемые неварьируемые параметры, f=l, 2, ..., р.
В математической модели силового трансформатора под у, например, могут подразумеваться напряжение КЗ, распределение ампер-витков по оси обмоток, изоляционные расстояния, уровни потерь КЗ и XX и т. д., а под z— цены на материалы, свойства материалов, стоимость потерь электроэнергии и другие параметры,
однозначно влияющие на критерий эффективности. Конкретные значения yi обычно устанавливаются стандартами и по мере улучшения свойств активных и изоляционных материалов, появления конструктивных и технологических новшеств пересматриваются. Отличительной особенностью этих параметров является то, что их оптимизация, как правило, требует обобщенного критерия эффективности, позволяющего определить оптимальные значения yi в применении к серии трансформаторов, отрасли в целом или, наконец, ряду отраслей народного хозяйства. При этом не исключено, что полученные с учетом этих соображений yi будут оптимальны и для конкретного типа трансформатора.
Величины Zf зависят от качества материалов, технологии производства, производительности труда не только в трансформаторостроении, но и в смежных отраслях. Вместе с у, а также номинальными параметрами трансформатора zf образуют группу исходных данных и условий на проектирование.
Подробнее рассмотрим количество и природу варьируемых проектных параметров х. При проектировании конкретной серии трансформаторов количество этих параметров вполне определенно по условиям задачи оптимизации и соответствует набору независимых (в математическом смысле) переменных. Это означает, что ни одна из этих переменных не может быть выражена через остальные при использовании любых уравнений математической модели трансформатора. Таким образом, число варьируемых параметров должно соответствовать максимальному количеству переменных, которые могут независимо друг от друга меняться при поиске экстремума целевой функции. Нередко для сокращения времени решения поиск ведется при фиксированных значениях некоторых параметров. В этом случае результат носит частный характер и используется только с указанием значений выведенных из оптимизации переменных.
Выбор варьируемых параметров при проектировании силового трансформатора неоднозначен. Рассмотрим два возможных набора варьируемых параметров для силовых двухобмоточных трансформаторов с катушечными обмотками и регулированием напряжения при отключенном трансформаторе, без возбуждения (ПБВ), идентичных с точки зрения математической модели.
Первый набор: число витков обмотки НН высота провода обмотки НН bпр1; ширина провода обмотки НН апр2; высота провода обмотки ВН bпр2, ширина провода обмотки ВН апр2; число катушек обмотки ННz1; число катушек обмотки ВН z2.
Второй набор:
индукция в стержне магнитопровода Вс; плотность тока в обмотке НН δ1;
отношение сторон прямоугольного провода обмотки НН k1,
плотность тока в обмотке ВН δ2;
отношение сторон прямоугольного провода обмотки ВН k2; высота обмотки НН Яг, высота обмотки ВН H2.
Добавляя в каждом случае диаметр стержня магнитопровода dc и число параллельных проводов в обеих обмотках п1 и n2, получаем по десять независимых переменных, предопределяющих как все параметры и характеристики рассчитываемого трансформатора, так и его конструктивное устройство. Различие между этими наборами состоит в том, что в первом случае все параметры имеют дискретную природу, во втором же — восемь переменных (включая диаметр стержня dc) непрерывны по своему характеру. Этот факт свидетельствует о возможности рационального выбора варьируемых параметров применительно к принятой вычислительной схеме. Так, используя метод перебора переменных, целесообразнее воспользоваться первым списком варьируемых параметров. Применяя градиентный и другие методы, основанные на дифференциальном исчислении, предпочтение следует отдавать второму набору. При изменении варьируемых параметров поиск оптимального варианта трансформатора производится в так называемой допустимой области, формируемой в основном ограничениями вида (4.2). Эти ограничения представляют предписываемые стандартами или техническими условиями требования на допустимые изменения основных характеристик и параметров трансформатора. Примерами таких ограничений при проектировании силовых трансформаторов являются:
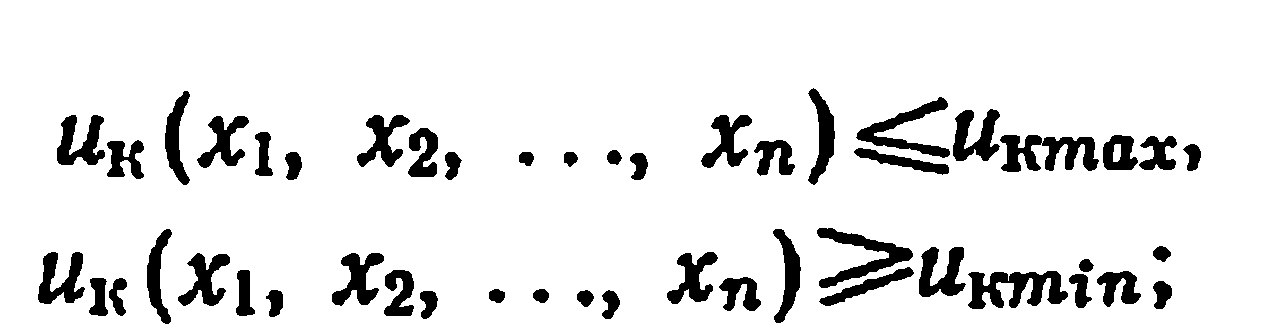
заданное напряжение КЗ с отклонением, равным ±(3-5)% расчетного,
(4.9)
(4.10)
заданные максимальные значения потерь КЗ и XX
![]()
(4.11)
(4.12)
заданные средние превышения температуры обмоток над температурой окружающего воздуха, а также заданное превышение температуры масла в верхних слоях

(4.13)
(4.14)
(4.15)
условия осевой и радиальной устойчивости обмоток

(4.16)
(4.17)
(4.18)
Эти ограничения формируют некоторую область В, представляющую в геометрической интерпретации гиперпространство сложной конфигурации. Допустимая область D, внутри которой ищется оптимальная точка X*, соответствующая минимальному значению целевой функции Ц=f(x1, Х2, .... хп*), получается при пересечении областей А и B(D=A-B). Объем допустимой области D, как показывают специальные расчеты, значительно меньше объема области А и составляет не более 0,001 объема последней.
В теории математического программирования особое место занимает вопрос о конфигурации допустимой области. Если удается установить, что допустимая область представляет выпуклое множество решений, то при условии выпуклости целевой функции можно утверждать, что любой относительный минимум является абсолютным (глобальным) минимумом.
Практически вид множества допустимых решений определяется по виду функций в левых частях ограничивающих условий (4.2). Это множество будет выпуклым, если функции Fi(x1, х2, .... хп) линейны или выпуклы.

В нашем случае функции в левых частях неравенств (4.9)—
- оказываются нелинейными, что подтверждается представлением этих функций в явном виде, выполненном с помощью ЭВМ. Для примера приведем полученные выражения для напряжения и потерь КЗ:
(4.20)
(4.21)
где коэффициенты  а остальные величины
а остальные величины
Н =Н1=Н2;
Sн — номинальная мощность трансформатора, кВ·А;
U1 — фазное напряжение обмотки НН, В;
U2 — фазное напряжение обмотки ВН, В;
α01 — изоляционное расстояние от стержня до обмотки НН, см;
α12 — изоляционное расстояние между обмотками, см;
dc — диаметр стержня магнитопровода, см;
Вс — индукция в стержне, Тл;
δ1, δ2 — плотности токов в обмотках НН и ВН, А/мм2;
k1, k2 — отношения сторон прямоугольного провода обмоток НН и ВН;
Я — высота обмоток, см;
n1, n2— число параллелей обмоток НН и ВН.
Для выпуклости функций Fi(x1, Х2, ..., Хn) необходимо, чтобы для любых двух точек X и У удовлетворялось неравенство
![]() (4.22) где
(4.22) где
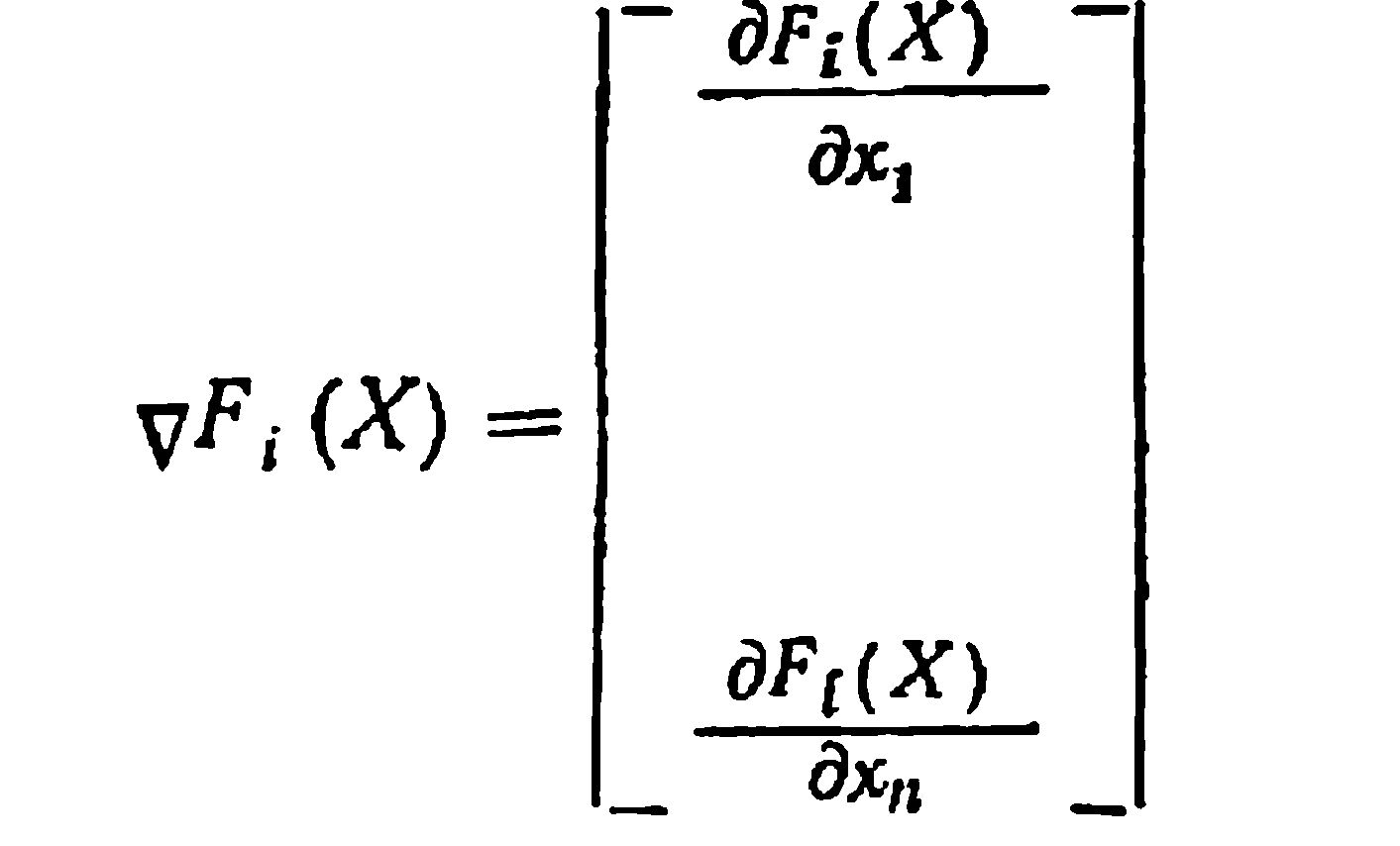
С целью экспериментальной проверки с помощью ЭВМ был проведен анализ выполнимости условия (4.22) по всему пространству области А. Полученные результаты свидетельствуют об удовлетворении неравенства (4.22) для всех рассматриваемых функций. Таким образом, с помощью машинного эксперимента удалось установить выпуклый характер функций, входящих в неравенства (4.9)—(4.19).
Чтобы установить, наконец, вид допустимой области D, приведем одну формулировку из теории математического программирования [69]: «множество Д всех точек, удовлетворяющих условиям
![]() (4.23)
(4.23)
![]()
выпукло, если в неравенствах со знаком выпуклые функции, а со знаком ≥ вогнутые функции для Х≥0». Все наши неравенства, (4.24)
получаем в левой части вогнутую функцию. Теперь мы вправе утверждать, что область допустимых решений, в которой отыскивается точка, соответствующая оптимальному исполнению трансформатора, является невыпуклой и, следовательно, абсолютный характер найденного экстремума не может быть гарантирован при использовании методов, предполагающих его единственность.
Для подтверждения приведенных теоретических выводов характер допустимой области исследовался экспериментально на примере трансформатора ТМ-1600/35.
Рассматривая вид допустимой области, мы пока пренебрегаем дискретностью ряда параметров в связи с предположением о дифференцируемости функций в левых частях неравенств (4.9)— (4.19). Поэтому все расчеты и построения допустимой области, как и теоретические выводы, осуществлялись для непрерывных варьируемых параметров. Так как графическая иллюстрация возможна только в двухмерном пространстве, то изображение допустимой области, имеющей десять измерений, выполнимо при фиксированных значениях восьми регулируемых параметров. В качестве таких значений приняты оптимальные величины. Таким образом, графическая иллюстрация области допустимых решений — это по существу сечение ее плоскостью, проходящей через оптимальную точку (рис. 4.1 и 4.2).
Фактор дискретности переменных, а также учет всех конструкторских и технологических требований еще больше усложняют картину, увеличивая несвязанность допустимой области, которая оказывается состоящей из большого числа изолированных точек, совокупности которых располагаются крайне неравномерно (в заштрихованных зонах рис. 4.1 и 4.2).
Из сказанного понятно, что множество допустимых решений математической модели силового трансформатора имеет весьма сложную структуру, что значительно усложняет поиск глобального экстремума при решении задачи оптимизации.
Конкретный вид целевой функции (4.3) в математической модели зависит от заданного критерия эффективности. При оптимальном проектировании силовых трансформаторов в качестве такого критерия обычно выбираются народнохозяйственные затраты Знх или стоимость трансформатора Ст:

(4.25)
(4.26)
где Рх — потери холостого хода; Рк — потери короткого замыкания; Qp — реактивная мощность; Мс — масса стали; mпр1 — масса провода обмотки НН с изоляцией; тпр2 — масса провода обмотки ВН с изоляцией; Рам — коэффициент амортизационных отчислений; Е'н — нормативный коэффициент экономической эффективности; Цс, Цпр1, Цпр2 — оптовая цена электротехнической стали и обмоточных проводов; ηс, ηпр — коэффициенты использования электротехнической стали и обмоточных проводов; Зс, Зоб, Зпр — удельные затраты по заработной плате на производство магнитопровода, обмоток и прочие работы; kB — нормативный коэффициент; Сэ, Ср — удельные затраты на возмещение потерь активной и реактивной мощностей; Твкл — период включения трансформатора; τ — время работы с номинальной нагрузкой.

Рис 4.1. Вид допустимой области в плоскости /С1/С2 (кружок с лучами — оптимальная точка)

Рис. 4.2. Вид допустимой области в плоскости (кружок с лучами — оптимальная точка)
Трансформатор с минимальным значением Знх является наи- лучшим с точки зрения общих затрат на его производство и эксплуатацию. Минимальному значению Ст соответствует другое исполнение трансформатора — с наименьшим расходом активных материалов.
Рассмотрим подробнее характер целевой функции, представив ее в явном виде. Для этого выразим через варьируемые параметры составляющие целевой функции:
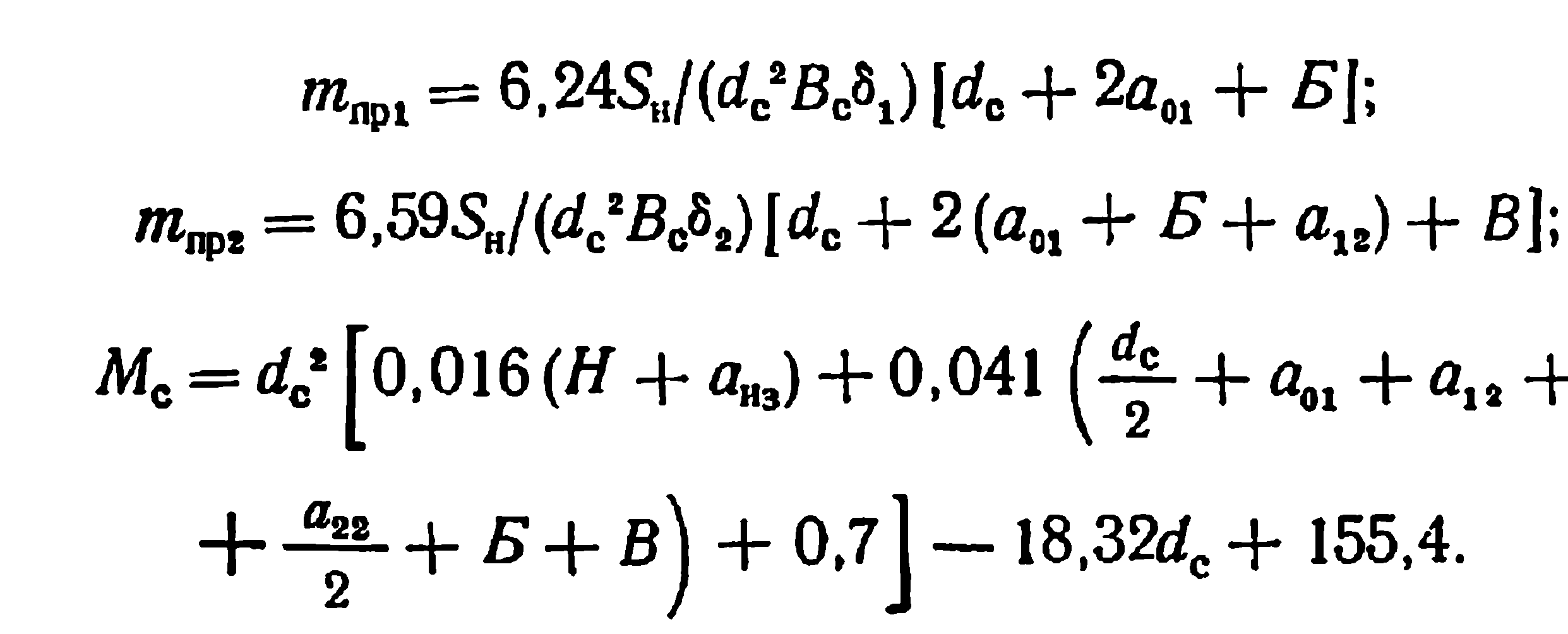
(4.27)
(4.28)
(4.29)
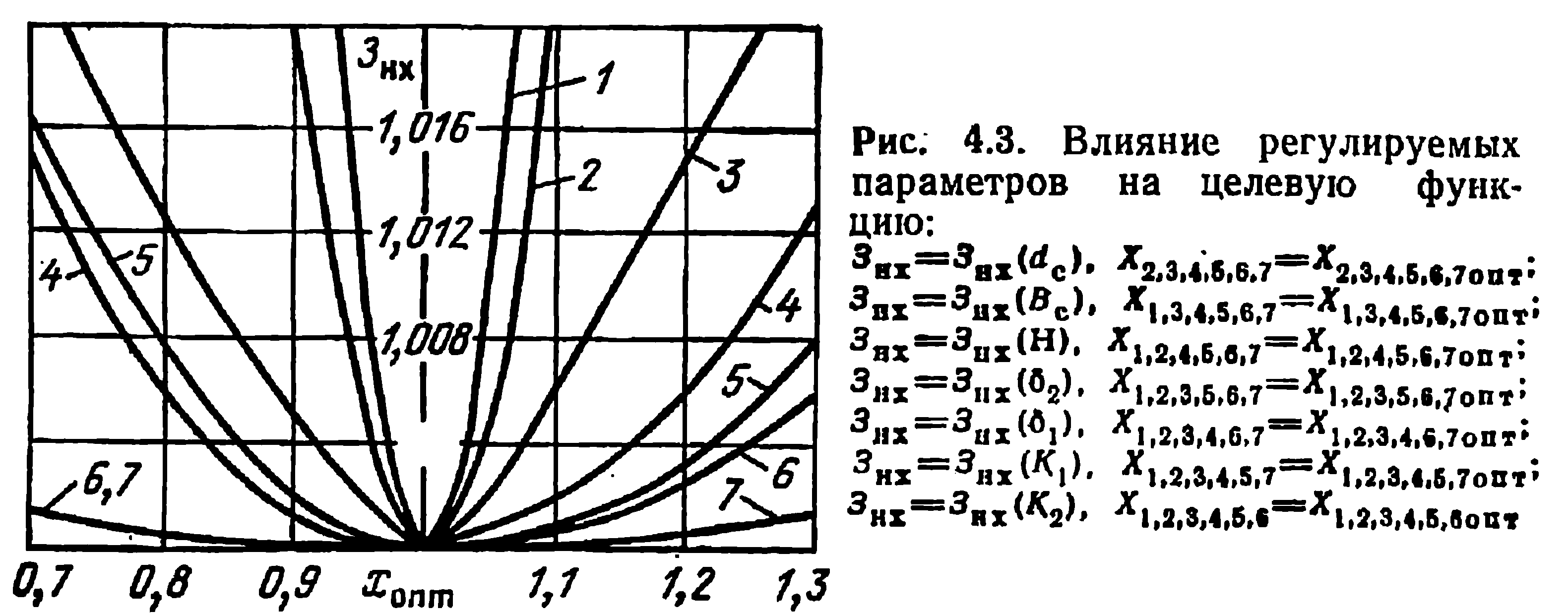
Из приведенных выражений видно, что Ст и Знх являются нелинейными функциями принятых варьируемых параметров. Если линейная целевая функция в геометрической интерпретации представляет гиперплоскость, которая с изменением целевой функции Ц параллельно перемещается в Еп, то нелинейность вызывает изменение вида геометрического аналога уравнения (4.8), становящегося гиперповерхностью, которая может быть не параллельна начальной. Этот факт уже сам по себе не гарантирует единственность экстремума даже при выпуклой допустимой области D.
Следующей причиной, затрудняющей поиск глобального экстремума, является значительное различие во влиянии регулируемых параметров на Ц, что предопределяет ее выраженный оврагообразный характер в пространстве Еп. Из рис. 4.3 видно, что наибольшее влияние на (выраженное в относительных единицах) оказывают dc и Вс, а от k1-2 целевая функция зависит весьма незначительно. Оврагообразный характер Ц затрудняет применение градиентных схем поиска. В этом случае первые же итерации выводят на «склон оврага», после чего движение к экстремуму идет по зигзагообразной траектории мелкими шагами (рис. 4.4). Кроме того, при переходе с одного «склона оврага» на другой необходимо изменять значение шага (как правило, уменьшать) во избежание зацикливания расчета (рис. 4.5). При этом требуется весьма тщательно оценивать величину производных, что затруднительно при отсутствии их аналитических выражений.
Влияние дискретности и производственных требований на целевую функцию иллюстрирует рис. 4.6.
Рис. 4.5. Поведение простейшего градиентного алгоритма при оврагообразном характере целевой функции

Рис. 4.4. Поведение релаксационного алгоритма при оврагообразном характере целевой функции
Пилообразный характер зависимости f (Xi) при промышленном проектировании, когда в качестве Xi выбираются дискретные параметры, предопределяет необходимость просчета целевой функции на всем интервале изменения каждого параметра. Иначе говоря, для сокращения вычислений не представляется возможным использовать унимодальный характер кривых f(Xi) без риска не достичь действительного экстремума.

Топография целевой функции Знх и границы допустимой области для трансформатора ТМ-1600/35 изображены на рис. 4.7, при этом в качестве аргументов взяты непрерывные параметры δ1 и δ2 . В отличие от рис. 4.2 при определении размеров области D вместе с оптимальными величинами остальных регулируемых параметров было зафиксировано значение высот обмоток, что привело к уменьшению размеров допустимой области, но сделало ее связной.
Соответствие между глобальным экстремумом и допустимой областью при решении задачи оптимизации может быть двоякого характера:
1. Глобальный экстремум находится на границе допустимой области. В этом случае ограничения определяют положение оптимальной точки и являются активными.

Рис. 4.7. Топография целевой функции и границы допустимой области трансформатора ТМ-1600/35
На рис. 4.7 таким оказывается ограничение по максимальному значению напряжения КЗ.
2. Глобальный экстремум находится внутри допустимой области. Ограничения не Оказывают никакого влияния на его положение и являются неактивными. К числу неактивных ограничений на рис. 4.7 относятся ограничения по потерям XX, среднему превышению температуры обмоток. Теоретически неактивные ограничения облегчают нахождение экстремума, так как уменьшают область неопределенности его существования. Практически же осуществить локализацию поиска только в пределах допустимой области, как правило, не удается, что объясняется ее весьма сложной конфигурацией. Поэтому для облегчения процесса поиска неактивные ограничения могут быть выведены из вычислительной схемы. При этом необходимо учитывать, что соответствие между глобальным экстремумом и границами допустимой области является подвижным, и ограничения, неактивные при одних номинальных исходных параметрах, при изменении последних в пределах той же математической, модели могут определять положение оптимальной точки, т. е. будут являться активными.

