В настоящее время проектировщики камер сгорания затрачивают основные усилия на проведение длительных и дорогостоящих экспериментов на полноразмерных моделях. Число таких экспериментов можно уменьшить, а процесс проектирования сделать существенно экономичнее за счет предварительного математического моделирования течения с использованием численных методов расчета. Моделирование процессов в камере сгорания с помощью феноменологических моделей, подкрепленное дополнительными фундаментальными экспериментами по выявлению основных физических закономерностей, сейчас вполне возможно, и, следовательно, его целесообразно использовать для минимизации времени на разработку камеры сгорания и ее стоимости.
В большинстве камер сгорания происходят рециркуляционные движения, и потому для детального расчета поля течения требуется применение итерационных методов. Математическая модель осесимметричных течений описывается системой двумерных эллиптических уравнений, которые формулируются либо в переменных завихренность—функция тока, либо в естественных переменных скорость — давление. Для численного интегрирования этих уравнений на ЭВМ требуется резервировать двумерные массивы памяти, а в качестве алгоритмов решения использовать поточечный итерационный метод Гаусса — Зайделя; линейный итерационный метод1) типа SIMPLE (квазинеявный метод решения уравнений, связанных через члены с давлением); линейные итерационные методы с использованием алгоритма TDMA (алгоритм обращения трехдиагональной матрицы). Основные различия между существующими вычислительными программами (и теми, которые еще могут быть созданы) следующие: сложность системы соотношений, описывающих физические процессы; требующаяся память ЭВМ; способ определения реперных точек разностных сеток, в которых задаются переменные; способ получения конечно разностных соотношений; метод решения.
1) Имеется в виду итерирование по совокупности узлов, расположенных вдоль линий некоторого координатного направления.— Прим. перев.
При разностной аппроксимации уравнений, записанных в переменных скорость — давление, обычно используются смещенные сетки, что было рекомендовано исследователями из Лос-Аламоса. В вычислительной гидродинамике для достижения точности и сходимости разностных схем и устойчивости итерационных алгоритмов весьма важно использовать хорошую аппроксимацию конвективных и диффузионных членов. При больших значениях сеточного числа Рейнольдса важно организовать передачу информации вдоль по потоку, например с помощью таких приемов, как разности против потока, гибридные схемы или лос-аламосский зигзаг, донорные ячейки и т. п.
Расчеты в переменных завихренность — функция тока.
Первые расчеты конечно-разностным методом стационарного осесимметричного закрученного факела с рециркуляционными зонами были, по-видимому, проведены Паном и Сполдингом [115]. Эти авторы для определения характеристик диффузионного факела в цилиндрической топке использовали численный метод интегрирования уравнений в переменных завихренность— функция тока [108]. Скорость химических реакций предполагалась достаточно большой, для того чтобы реализовался режим диффузионного горения, и потому для расчета использовалась система четырех дифференциальных уравнений в частных производных для переменных ф, ω/r, wr, f. Для определения турбулентной вязкости использовалась простая формула![]()
где L — длина участка камеры от начала до поджатия на выходе. Как и при расчете изотермических течений, коэффициент К полагался равным 0,012, что обеспечивает правильное распределение параметров в турбулентных струях без закрутки. Необходимо особо подчеркнуть, что в настоящее время существуют более совершенные модели турбулентных реагирующих течений, т. е представленные результаты следует рассматривать как иллюстративные.
На рис. 4.86 представлены результаты расчетов [115] течения в цилиндрической камере сгорания, которая обладает многими особенностями, характерными для реальных камер: топливо и воздух подаются с одного конца, выхлоп продуктов сгорания происходит с противоположного, канал для подвода воздуха представляет собой кольцо, окружающее канал подвода топлива, имеются устройство для закрутки воздуха на входе и толстая кольцевая вставка между каналами подвода воздуха и топлива.

Рис. 4.86. Распределения параметров при двух различных значениях интенсивности закрутки потока воздуха [115].
Степень диффузорности D/d равна двум. При заданных условиях, таких, как угол установки закручивающих лопаток, скорость топлива на входе Up (которая также влияет на
отношение воздух/топливо), и при постулировании отсутствия или наличия химических реакций можно рассчитать функцию тока, распределения скоростей и температуры, состав смеси в камере. На рис. 4.86 показаны линии тока (фигуры с номера ми I, IV), изотермы (II, V) и изолинии окружной скорости (III, VI) для двух различных степеней закрутки воздуха на входе, слабой закрутки (фигуры с номерами I, II, III) и сильной закрутки (IV, V, VI). В последних двух случаях полученные в расчете поля параметров сильно различаются. Сильная закрутка приводит к появлению тороидального вихря в центре камеры в дополнение к рециркуляционной зоне вблизи входного сечения, появление которой вызвано внезапным расширением поперечного сечения. Сильная закрутка также укорачивает факел пламени. Оба этих эффекта хорошо известны специалистам по камерам сгорания, которые стараются использовать рециркуляцию горячих продуктов сгорания и плохообтекаемую форму рециркуляционной зоны как средство повышения эффективности процесса горения. Фигуры с номерами III и IV на рис. 4.86 показывают, как затухает окружная скорость вдоль осевого направления. Отметим, что в случае с сильной закруткой окружная скорость затухает в осевом направлении быстрее.
В более поздней версии программы расчета в переменных φ — ω, разработанной в Имперском колледже [108] под названием PISTEP, в методику вычислений внесен ряд усовершенствований. В работе [116] она использована для расчета закрученного потока при истечении в канал с внезапным расширением и, кроме того, в целях анализа влияния неизотропности турбулентности, для чего в некоторых случаях использовалась двухпараметрическая kт—W-модель турбулентности, где W —к/l. В тех областях, где продольный градиент квадрата окружной составляющей скорости играл определяющую роль, вводились определенные модификации, которые призваны были устранить неустойчивость, обусловленную слагаемым источником в уравнении для завихренности. Нижняя релаксация оказалась неэффективной; проблему удалось решить, хотя и за счет снижения скорости сходимости, с помощью специально разработанного метода согласования циркуляций МРСА. В этом методе на распределения φ и ω накладываются требования удовлетворения теореме о циркуляции. Аналогичный закрученный поток без горения со смешением соосных струй изучался при использовании двухпараметрической модели турбулентности, нс учитывающей анизотропию, в работе [18], где получены интересные результаты о влиянии входных параметров. Метод нашел применение и в расчетах закрученного диффузионного факела в цилиндрической топке работающей на газообразном топливе; при этом вновь использовалась простая алгебраическая модель турбулентной вязкости [118].
Позднее аналогичное течение, а именно диффузионный факел в камере сгорания газовой турбины, изучалось в работе [119]; на рис. 4.87 приведены результаты одного из вариантов расчета.

Рис. 4.87. Результаты расчета линий тока в камере сгорания [119]: угол установки лопаток завихрителя φ = 60°; ир = 0,5u; отношение воздух/топливо α' — 30.
1 — воздух; 2 — топливо; 3 — граница факела.
Размеры устройства таковы, что при одинаковых скоростях истечения горючего из первичного контура (иР) и
воздуха нз вторичного контура (иs) получается стехиометрическое соотношение компонентов (отношение воздух/топливо afr= 15). Следует особо подчеркнуть, что сейчас уже разработаны более совершенные модели турбулентных реагирующих потоков, в связи с чем результаты этих расчетов следует рассматривать как иллюстративные. В качестве входных данных использованы следующие: давление р = 2,5 МПа, температура Т = 850 К и и = 36 м/с.
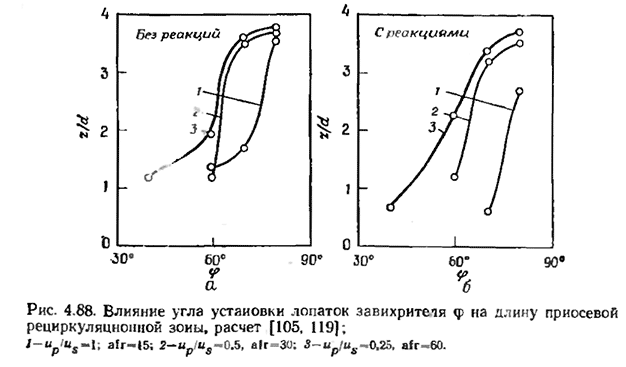
Результаты расчетов [105, 119) позволили обнаружить некоторые интересные особенности явления и показали наличие существенной разницы в структуре незакрученного и сильнозакрученного течений (угол установки лопаток завихрители φ = 60° приблизительно соответствует параметру закрутки S= 1,2). Сильная закрутка приводит к появлению ЦТВЗ в центре камеры, а также укорачивает факел.
Угол установки лопаток завихрители является решающим фактором существования (или отсутствия) приосевой рециркуляционной зоны и определяет се размеры. На рис. 4.88 показана длина этой зоны в зависимости от угла установки лопаток φ при различных значениях иР (а следовательно, и различных значений afr). На рис. 4.88,а представлены результаты для случая без химических реакций, на рис. 4.88,б—с реакциями. В обоих случаях при фиксированном значении иР (afr) длина зоны возрастает с ростом φ. Уменьшение иР при фиксированном значении φ способствует образованию зоны и увеличению ее длины.
Следует также отметить, что в потоке без реакций зона, как правило, протяженнее, а при наличии химических реакций расширение газа и увеличение скорости способствуют укорачиванию зоны по сравнению с зоной в потоке без горения и в некоторых случаях приводят к ее разрушению (например, при φ° = 60, Up = Us). Несмотря на это, длины рециркуляционных зон при малых значениях иР (больших значениях afr) вполне сопоставимы, особенно при больших степенях закрутки. Такое поведение длины рециркуляционной зоны объясняется тем, что при малых иР и большой закрутке факел пламени короткий и находится в верхней по потоку части зоны, а не окружает ее. Расчет, так же как и эксперимент, показывает, что при уменьшении и г (увеличении afr) или увеличении угла φ, или при одновременном изменении этих факторов монотонно уменьшается длина факела и улучшается (становится более равномерным) распределение температуры поперек выходного сечения камеры сгорания. Для примера на рис. 4.89 показано влияние иР и φ на длину факела. При укорочении факела длина области перемешивания, в которой горячие продукты сгорания могут перемешиваться с более холодным воздухом, возрастает, и это способствует выравниванию распределения температуры поперек выходного сечения камеры, на что указывают измеренные значения температурной неравномерности, определенной как разность максимальной и средней температур на выходе, отнесенная к величине подогрева.

Проводя некоторое обобщение, можно сказать, что появлению приосевой рециркуляционной зоны и увеличению ее размера способствуют увеличение D/d, наличие центрального тела перед входом в камеру (dh > 0), увеличение dh/d, уменьшение скорости в первичном контуре (что также смещает зону вверх по потоку), увеличение параметра закрутки или угла установки лопаток завихрители, подавление химических реакций. Оптимальное значение параметра закрутки в камерах сгорания, обеспечивающее рациональные размеры рециркуляционной зоны и умеренный уровень гидравлических потерь, составляет примерно S = 1,15, что соответствует углу установки лопаток завихрители φ = 60° (при этом D/d = 2).
В работе [126] указывается, что для других значений D/d при моделировании потока вниз по течению от входа в качестве параметра подобия лучше использовать параметр S, рассчитанный по диаметру камеры D, а не по диаметру сопла d.
В ряде работ [120, 121] использовался более сложный подход для описания кинетики химических реакций. В работе (120) рассмотрены уравнения жесткой кинетики, проанализированы два метода расчета многомерных течений и проведен расчет двумерного течения с учетом кинетики разложения Н2O2. Осесимметричное течение в камере сгорания газовой турбины рассчитано в работе [121] с помощью простой алгебраической модели турбулентности. Программа расчета представляет собой существенно переработанный вариант основной версии, который включает модуль решения эллиптических уравнений методом блочной релаксации (FREP) и эмпирическую модель для турбулентной вязкости, являющуюся усовершенствованием модели пути смешения, но с учетом анизотропии. Использованы предположение о локальном химическом равновесии, обычный способ расчета конечных скоростей образования оксида азота NO и четырехкомпонентная модель излучения, а также предприняты специальные шаги для подробного моделирования распыления. Результаты, полученные при моделировании течения в реальной камере сгорания, несколько разочаровывают. Например, на рис. 4.90 изображены рассчитанные поля температур в сопоставлении с экспериментальными данными для берклеевской трубчатой камеры [ 127] Более поздние версии программы, называемые GFREP и GRISTY, включают двухпараметрическую kT — ε-модель турбулентности и модели испарения и горения капель.
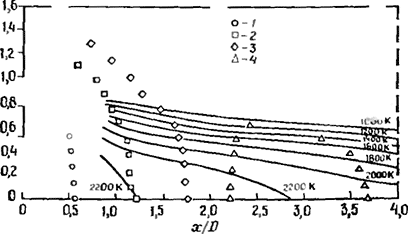
Рис. 4.90. Сопоставление полученных в расчете (линии) [121] и в эксперименте («точки») [127) распределений температуры в трубчатой камере сгорания. Эквивалентное отношение равно 0.205.
1 - Т = 600 К; 2 - T = 1200 К; 3 - Т = 1600 К; 4 — T = 1800 К.
Совсем недавно авторы этой работы перешли к расчетам полных трехмерных течений в переменных и—v—w—р (эти методы рассмотрены в гл. 6).

Рис. 4.91. Рассчитанные и измеренные распределения температуры (а) и концентрации окиси азота (б) в реакторе со струей во встречном потоке [125].
При расчете поля течения в камере сгорания твердотопливного прямоточного реактивного двигателя [123], где камера имеет внезапное расширение, для обеспечения устойчивости численного счета потребовалась значительная модификация алгоритмов. В этой программе использовалась двухпараметрическая модель турбулентности, а моделирование течения обеспечивалось путем задания соответствующих граничных условий, учитывающих эмиссию топлива и подвод массы. С помощью другой модификации программы моделировалось рециркуляционное движение нереагирующей смеси водорода с воздухом в канале. В этом случае вторичный поток подавался через боковые стенки секции с внезапным расширением; получающаяся здесь большая угловая рециркуляционная зона похожа на зону в камере с внезапным расширением и осевым подводом.
Течение с химическими реакциями, реализующееся при вдуве струи аммиака навстречу воздушному потоку, подробно изучалось в работе [125], где расчеты вначале проводились в переменных φ — ω с использованием двухпараметрической модели турбулентности. Результаты расчета на сильно неравномерной сетке с простои кинетической моделью брутто реакций хотя в определенной степени и согласуются с опытом, однако неточны в деталях, что видно из данных рис. 4.91 на примере распределения температур и концентраций продуктов сгорания. В работе [125] в качестве возможной причины несоответствия называлось несовершенство модели турбулентности. Выполненные в работе [133] расчеты в переменных r — и — ν показывают, что такой подход выглядит более обещающим, обеспечивает большую гибкость модели, хотя процесс горения здесь пока не рассматривался.
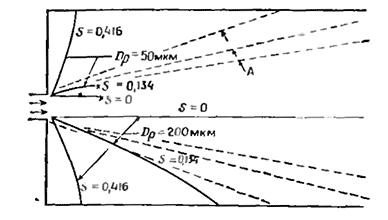
Рис. 4.92. Траектории частиц различных размеров в турбулентной закрученной струе, распространяющейся в ограниченном пространстве [129]:
А — граница струи; крестиками отмечены точки на траекториях, соответствующие выгоранию частиц.
В работе [128] рассмотрено течение воздуха с частицами угля, служащего топливом. С использованием приближенного описания поля течения рассчитаны траектории горящих угольных частиц. Траектории частиц, имеющих размеры 50 и 200 мкм, в потоках с тремя различными значениями параметра закрутки, рассчитанные в работе [129], представлены на рис. 4.92. В незакрученном потоке траектории обоих типов частиц почти прямолинейные и частицы не попадают в зону обратных токов. Даже частицы с меньшим размером практически не подчиняются аэродинамическому воздействию. При малой закрутке меньшие частицы все еще выгорают в струе, а большие попадают на стенку не догорев; их остаточная масса составляет 6 %. Чтобы избежать перегрева стенок при попадании частиц, следует уменьшить степень закрутки или размеры частиц Очевидно, что закрутка, отвечающая значению S = 0,416, является слишком большой для данной камеры сгорания при рассматриваемых размерах частиц. Проведенные исследования позволили сделать вывод, что допущение о равенстве скоростей газа и частиц может вносить серьезные погрешности в расчеты.
Расчеты в переменных скорость — давление (и — υ — р)
При использовании вычислительных методов, в которых решаются уравнения, записанные в переменных φ — ω, возникают трудности при проведении расчетов на неравномерных сетках при рассмотрении течений с сильной закруткой и большими градиентами плотности. В последнее время развитие вычислительных методов связано с использованием естественных переменных и — v — р вместо φ— ω. Над созданием методов решения уравнений, записанных в естественных переменных, наиболее плодотворно работают две группы исследователей: из Лос-Аламосской исследовательской лаборатории (LASL), Лос-Аламос, Нью-Мексико, и из Имперского колледжа, Лондон, Англия. Приведем сокращенные названия основных программ, созданных первой группой для расчета нестационарных течений: MAC (метод маркеров и ячеек), SMAC (упрощенный метод MAC), SOLA (алгоритм решения) и др. Основные программы, созданные второй группой для расчета стационарных течений: SIMRLE (квазинеявный метод решения уравнений, связанных через члены с давлением), EASI (метод интегрирования эллиптических уравнений для осесимметричных течений), TRIC и TRIP (методы расчета трехмерных течений с рециркуляционными зонами в декартовой и цилиндрической системах координат), TEACH (расчет характеристик потоков с реальными свойствами на основе численного решения эллиптических уравнений), CHAMPION (программа расчета тепло- и массопереноса), PHOENICS (серия программ для численного интегрирования параболических, гиперболических и эллиптических уравнений) и др.
Метод ICE (неявный метод расчета движения сплошной среды в эйлеровых переменных), созданный в LASL, представляет собой неявный конечно-разностный численный метод, в котором поле давления на следующем временном слое определяется из решения соответствующего уравнения Пуассона [130]. В отличие от этого в программе SOLA использован иной подход — явный метод, в котором поле давления определяется путем последовательного (от точки к точке) согласования скоростей на границе ячейки и давления. С помощью метода LASL — ICE в работе [131] исследовалось ламинарное нестационарное течение сжимаемого газа с набором перемешивающихся и реагирующих компонент. Исследование было предпринято главным образом для того, чтобы проанализировать свойства осесимметричных течений со стационарными условиями на входе и химическим превращением компонент, т. е. течений, в которых проявляется сильное влияние физико-химических процессов на гидродинамику. Рассматривались, например, такие ситуации разгон потока в бесконечной трубе; течение в ударной трубе; периодические пульсации на фоне стационарного в среднем течения; течение, реализующееся при осевом входе равномерного потока в длинные и короткие трубы; оторвавшаяся струя в диффузоре с внезапным расширением. К сожалению, не удалось удовлетворительно описать течения с большими скоростями тепловыделения и сильным воздействием физико-химических процессов на гидродинамику.

Рис. 4.93. Профили продольной скорости в незакрученном потоке с горением [109]:
1, 3. 3—расчеты с использованием соответственно моделей горения I. 2, 3; точки — экспериментальные результаты.
Численный метод, разработанный в Имперском колледже и реализованный в программе СЕАСН [135], применялся
в работах [106, 100, 132] для расчета турбулентных закрученных потоков с химическими реакциями. В этих исследованиях использовались довольно совершенные модели турбулентности (двухпараметрическая kT — ε-модель) и горения (диффузионная модель реактора с интенсивным смешением). В работе [136] решались уравнения не только для переменных и — v — — w — р — kТ — ε — h — тfи — f, но также для среднеквадратичных значений пульсаций концентрации лимитирующего реагента и корреляций между пульсациями параметров состояния и массовых концентраций компонент, участвующих в реакциях по схеме Зельдовича. Полученные во всех упомянутых работах результаты расчета осесимметричных закрученных потоков в топках вполне удовлетворительные.
Расчеты проводились с использованием трех моделей горения: модель 1 —диффузионное горение; модель 2 — диффузионное горение с конечной толщиной зоны реакции за счет турбулентного характера течения, параметр g (g = (f'2)f/2—среднеквадратичное значение пульсаций концентрации) рассчитывался с помощью соответствующего дифференциального уравнения в частных производных; модель 3 — горение с конечными скоростями реакций, которые определяются по наименьшему из двух значений: полученного из закона Аррениуса и по модели распада вихрей, параметр g определяется либо с помощью дифференциальных уравнений с частными производными, либо по алгебраической модели, соответствующей равновесному решению дифференциальной модели.
На рис. 4.93 и 4.94 приведены примеры расчетов продольной скорости, заимствованные из работы [109], для сечений x/D, = 1,0 и 1,5 при значениях параметра закрутки S = 0 (рис. 93) и S = 0,52 (рис. 4.94). Как показывают эти данные, в потоке с закруткой образуется приосевая ЦТВЗ, а вниз по потоку профили скорости выравниваются. Сопоставление с экспериментальными данными показывает, что модель горения 2 дает несколько лучшее описание течения, чем модель 3, а модель 1 хуже, чем модель 3. Отсюда следует, что неточности детального моделирования, применяемого в модели 3, оказываются более существенными, чем учет конечности скоростей химических реакций. Рассчитанные поля температур находятся в качественном соответствии друг с другом, но, к сожалению, отсутствуют экспериментальные данные для сопоставления.
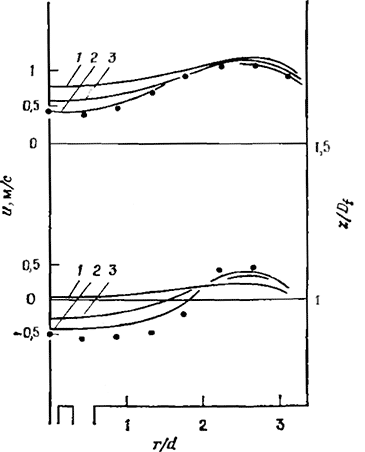
Рис. 4.94. Профили продольной скорости в закрученном потоке (S = 0,52) с горением [109] (обозначении те же, что на рис. 4.93).
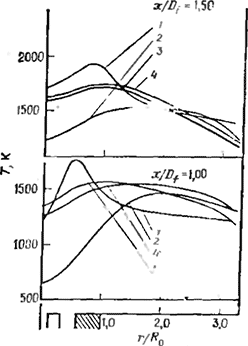
Рис. 4.95. Профили температуры в незакрученном потоке с горением [109]: 1, 2. 3-- расчеты с использованием соответственно моделей горения 1, 2, 3 ,4 — расчет с использованием модели горения 3, в которой g определяется по алгебраической формуле.


Рис. 4.97. Распределение кинетической энергии турбулентности вдоль оси незакрученного потока с горением [ 109]:
Рис. 4.96. Профили температуры в закрученном потоке (S = 0,52) с горением [109] (обозначения те же, что на рис. 4.95).

Рис. 4.98. Распределение кинетической энергии турбулентности вдоль оси закрученного потока (S = 0,52) с горением [109] (обозначения те же, что на рис. 4.97).
Рассчитанные профили осредненной температуры представлены на рис. 4.95 и 4.96.
На рис. 4.97 представлено распределение удельной кинетической энергии турбулентности вдоль оси камеры в потоке без закрутки; за исключением начального участка, результаты расчета находятся в удовлетворительном соответствии с экспериментальными данными. Расхождение на начальном участке на расстоянии до 0,3D, может быть объяснено наблюдаемым в опытах небольшим отходом факела от входного сечения камеры вследствие ускорения потока, в результате чего воспламенение задерживается на расстоянии, равном 0,15Df. В расчете же область начального ускорения расположена очень близко к входному сечению камеры, а за ней следует торможение по мере того, как центральная струя с меньшей плотностью проникает в окружающее пространство и происходит воспламенение. На рис. 4.98 показано распределение удельной кинетической энергии турбулентности в потоке с параметром закрутки S = 0,52. В этом случае стабилизация пламени происходит на горелке без отхода факела, и модель лучше согласуется с экспериментальными данными. Видно, что модель 2 хорошо согласуется с экспериментальными данными, представленными на рис. 4.97 и 4 98, но в потоке с закруткой это соответствие значительно лучше. Наконец, на рис. 4.99 показано, как затухает окружная скорость в закрученном потоке (S = 0,52) с горением.
Эти и другие, как экспериментальные, так и расчетные данные, ясно показывают, как влияет закрутка на распределение пламени в топках. Закрутка приводит в общем случае к выравниванию распределения скорости в поперечном сечении камеры, расширению области высокой температуры и смещению ее от оси, повышению начального и понижению конечного уровней энергии турбулентности.

Рис. 4.99. Профили окружной скорости в закрученном потоке (5 — 0,52) с горением [104] (обозначения те же, что на рис. 4.93)
Аналогичная вычислительная программа, в которой используются современные модели, была разработана в работе [106] и использована для исследования сильнозакрученного стесненного потока с горением предварительно перемешанных компонент. В расчетах использована kT— ε-модель турбулентности, горение описывается простой экзотермической реакцией, идущей в одну стадию, скорость которой определяется по модели распада вихрей. Поток в кольцевом канале с наружным диаметром кольца d и внутренним dh проходит через лопаточный завихрители с лопатками, установленными под углом φ, в результате чего он приобретает закрутку с равномерным профилем окружной скорости w, а затем истекает в цилиндрическую камеру с внезапным расширением диаметром D и длиной L. В эксперименте d= 0,098 м, σh = 0,33d, D = 5d, l= 15d. Среда представляет собой смесь светильного газа и воздуха; газ характеризуется параметрами mfu= 0,025, Mfu = 14, Hfu = 26,6 МДж/кг, стехиометрическое отношение (кислород/топливо) s = 3,5. Химические реакции происходят ниже по потоку от лопаточного завихрители, и цель исследования состояла в изучении влияния угла установки лопаток завихрители на распределения продольной в окружной скоростей, температуры, форму и размеры приосевой рециркуляционной зоны.
Результаты показывают, что в общем случае увеличение угла закручивания приводит к укорочению и расширению факела, к повышению интенсивности процесса горения, и к увеличению темпа вырождения продольной и окружной скоростей. Характер влияния закрутки зависит от того, существует ли рециркуляционная приосевая зона или нет, а, как было показано и в расчетах и в экспериментах, зона появляется при φ > 30°.
При слабой закрутке в отсутствие рециркуляции увеличение угла установки лопаток завихрители приводит к такому же увеличению ширины струи, как и в случае свободной струп с горением. С появлением рециркуляции при больших углах установки лопаток ширина струи в канале нарастает значительно быстрее, чем в случае свободного истечения.

Рис. 4.100. Влияние угла установки лопаток завихрители на длину приосевой рециркуляционной зоны и длину факела [106].
Сплошная линия — рециркуляционная зона; штриховая — факел; кружки — расчетные данные; крестики — экспериментальные результаты.
На рис. 4.100 показаны расчетная и экспериментальная зависимости длины приосевой рециркуляционной зоны и длины факела от угла установки лопаток завихрители φ. Видно, что, когда φ превышает 30°, появляется рециркуляционная зона, длина которой при больших углах установки лопаток завихрители остается постоянной. В целом соответствие расчета и эксперимента удовлетворительное, хотя в расчете длина зоны оказывается заниженной. Картина линий тока и форма границ рециркуляционной зоны похожи на соответствующие картины в потоке без реакций (см рис. 4.76). С ростом закрутки, приводящей к появлению приосевой рециркуляционной зоны и росту интенсивности турбулентности, факел пламени укорачивается.
Усовершенствованный вариант программы [132, 134], аналогичной рассмотренным выше, был использован для расчета течений в камерах сгорания газовых турбин, камер с внезапным расширением и с боковым вдувом. Решалась система уравнений для определения и, v, w, р, двух параметров турбулентности (кт и ε) и трех параметров для моделирования факела пламени предварительно перемешанных компонент. Такой метол позволяет моделировать характерные особенности потока в реальных камерах и делать на основе расчетов практические выводы.
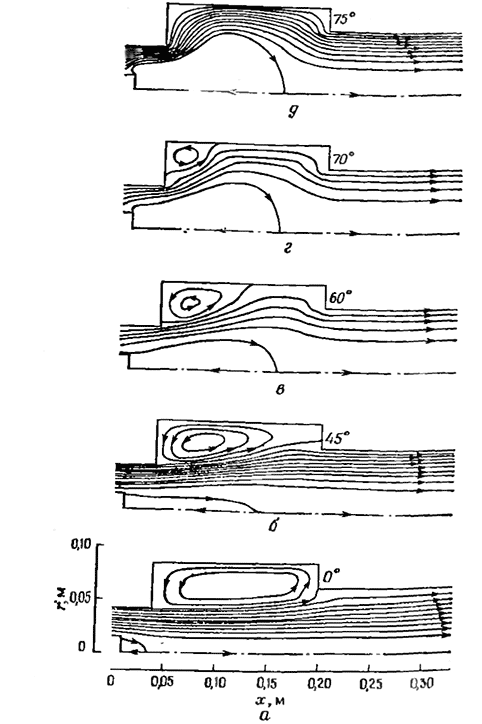
Рис. 4.101. Результаты расчета линий тока в изотермическом потоке в камере сгорания с внезапным расширением при вариации закрутки [132]:
а—угол установки лопаток завихрители φ=0°; б—φ=45°; в-φ=60°; г—φ=70°; д—φ=75°.
Результаты расчетов дают представление о влиянии отдельных параметров, таких, как интенсивность закрутки, характеристики секции, устанавливаемой для увеличения размеров рециркуляционной зоны («защелки»), параметры, характеризующие поперечный вдув в камеру, на поле течения и характеристики камеры сгорания (т. е. на распределения скорости, температуры, концентрации компонентов, параметры рециркуляционных зон, размеры и форму факела, интенсивность процесса горения). Несмотря на присущие этому методу неточности, связанные с недостаточным пониманием физических процессов в турбулентных реагирующих потоках и с предположением об осесимметричности течения, проведение таких расчетов весьма полезно для анализа структуры потока в целях определения степени конструктивного совершенства устройства.

Рис. 4.102. Результаты расчета линии тока и поля направлений вектора скорости в соосных струях, распространяющихся в канале с внезапным расширением [132].
Для примера на рис. 4.101 показаны линии тока в изотермическом потоке, характеризующие картины течения, реализующиеся по мере роста параметра закрутки при увеличении угла установки лопаток завихрители. В незакрученном потоке (рис. 4.101, а) угловая рециркуляционная зона заполняет полость выступающей наружу секции камеры. При закрутке потока появляется ЦТВЗ, а размер угловой рециркуляционной зоны уменьшается, как показано на рис. 4.101,б. При дальнейшем росте угла установки лопаток завихрители происходят увеличение размеров приосевой зоны и уменьшение угловой зоны (рис. 4.101,в—4.101,д). В потоке, закрученном лопатками с углом установки 75°, угловая рециркуляционная зона исчезает. Такое сильное отклонение истекающего потока к торцевой стенке при высокой интенсивности закрутки наблюдалось исследователями в реальных камерах сгорания, но количественной информации о данном явлении пока недостаточно.
Определенную проверку возможностей расчетной программы и оценку ее точности можно провести путем сопоставления результатов вычислений с экспериментальными данными по распределениям параметров в соосных струях, распространяющихся в канале с внезапным расширением. На рис. 4.102 показаны рассчитанные линии тока, направления вектора скорости (стрелка указывает только направление) и границы рециркуляционных зон в потоке, идентичном по параметрам на входе экспериментально исследованному в работе [137]. Отметим наличие угловой рециркуляционной зоны, обусловленной внезапным расширением канала, и ЦТВЗ, появляющейся вследствие неравенства потоков массы в центральной и периферийной струях. Поток массы в периферийной струе существенно превышает поток в центральной.
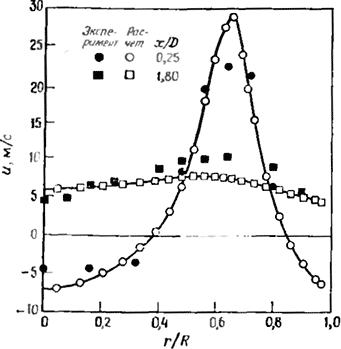
Рис. 4.103 Профили продольной скорости в соосных струях, распространяющихся в канале с внезапным расширением [132].
На рис. 4.103 сопоставлены расчетные и экспериментальные распределения по радиусу продольной скорости в двух сечениях: x/D = 0,25 (проходящем через обе рециркуляционные зоны) и χ/D — 1,8 (ниже по потоку от обеих зон). Соответствие расчета и эксперимента следует признать хорошим, особенно принимая во внимание, что информации о профилях скорости и характеристиках турбулентности на входе было недостаточно, а эти параметры, как известно, оказывают решающее влияние на точность моделирования. Эти и другие результаты дают основание считать, что расчетный метод позволяет хорошо моделировать течения с особенностями, характерными для камер сгорания, т. е. главным образом с внутренними и внешними рециркуляционными зонами.
В центральной струе оказывается недостаточным, чтобы преодолеть градиент давления, появляющийся вследствие внезапного расширения периферийного потока. В результате этого взаимодействия образуется ЦТВЗ. Оба типа рециркуляционных зон наблюдаются в реальных камерах сгорания, в которых, кроме того, потоки закручены и идут химические реакции. Проблема расчета таких течении подробно рассматривалась в работах [132, 134], но вначале полезно определить точность расчетов в простейших ситуациях.
Рассматриваемый алгоритм [132] позволяет также рассчитывать закрученные потоки с химическими реакциями На рис 4 104 показаны рассчитанная и полученная в эксперименте [136] картины изотерм в диффузионном закрученном факеле при параметре закрутки S = 0,3 и давлении 380 кПа. Видно, что в ЦТВЗ, особенно вблизи центра вихря, наблюдается высокая температура. Таким образом, имеется качественное соответствие результатов. Аналогичные распределения параметров получены расчетом для факела пламени предварительно перемешанных компонент; к сожалению, детальные экспериментальные данные отсутствуют. Однако и в этом случае имеется

Рис. 4.104. Изотермы в соосных закрученных струях при диффузионном горении [132].
Сплошные липни — результаты расчета: штриховые — экспериментальные данные, цифры на изотермах указывают температуру в кельвинах.
качественное согласие результатов с данными, полученными при визуализации потока.
Проведенные в последнее время исследования отдельных течений, характерных для камер сгорания [134], выполненные с использованием рассматриваемой здесь вычислительной программы COSMIC (программа расчета закрученных реагирующих потоков в камерах сгорания), показали целесообразность применения расчетных методов при проектировании камер, В качестве базовой конфигурации рассматривалась камера с кольцевым лопаточным завихрителем с углом установки лопаток 70. Из завихрители поток попадает в предкамеру, за которой следует основная камера с внезапным расширением. Поток на входе представляет собой стехиометрическую смесь метана и воздуха, в которой химические реакции начинаются ниже по потоку за сечением входа в камеру. Для анализа структуры потока с помощью ЭВМ рассчитывались и графически изображались линии тока. По сравнению с соответствующим случаем нереагирующих потоков размер угловой рециркуляционной зоны при горении уменьшается незначительно, а приосевая рециркуляционная зона становится существенно меньше, с большими скоростями рециркуляционного движения и меньшим потоком массы. Химические реакции, расширение газа и соответствующее увеличение продольной скорости способствуют укорочению приосевой зоны, а медленно движущийся газ получает ускорение, направленное к оси. В работе [134] уделено внимание изучению возможностей использования вычислительных методов для проектирования камер сгорания и рассмотрено влияние конструктивных особенностей камер на их характеристики, а также влияние таких конструктивных
параметров, как отношение диаметров основной камеры и пре камеры, размеры завихрители (внутренний и наружный радиусы), поджатие выходного сечения, характеристики двойного концентрического завихрители с противоположной закрути потоков, форма профиля концентрации топлива.
В работе [133] проведено полезное расчетно-экспериментальное исследование реактора со струей во встречном потоке, т. е. такого течения, где влияние граничных условий минимально. Изложены результаты параметрического исследования влияния исходных параметров математической модели на параметры, определяемые в расчетах. Изучалось влияние типа модели турбулентности, параметров соответствующих моделей, размеров ячеек конечно-разностной сетки, граничных условий в рециркуляционной зоне, профилей составляющих скорости, значений kт и е на входе, соотношения потоков массы основного течения и струи.
Кроме рассмотренных разработаны и другие методики расчета осесимметричных течений в естественных переменных, которые позволяют определять характеристики закрученных потоков и представляют большой интерес для проектировщиков камер сгорания. Уайтлоу и др. [138, 139] провели расчеты и сопоставление с экспериментальными данными характеристик течения в камере с внезапным расширением при горении керосиновоздушной смеси. В работе [140] рассчитано и сопоставлено с экспериментальными данными [141] течение в соосных закрученных струях с закруткой в одинаковом и противоположном направлениях, распространяющихся в ограниченном пространстве; при этом изучалось явление распада вихря В работах [142, 143] проводились расчеты различных типов течений с горением и без горения в целях проверки и усовершенствования моделей турбулентности и моделей горения, применимых к описанию процессов в камерах сгорания авиационных газотурбинных двигателей. Необходимые для сопоставления экспериментальные данные получены в работе [144]. Расчеты по единой методике закрученных потоков с горением и без горения выполнены соответственно в [145] и [112]. Лилли и др. [110] провели расчетно-экспериментальное исследование «крученных потоков, истекающих в большую камеру с внезапным или плавным расширением. Теми же авторами проведены расчеты ряда других течений: закрученного потока в камере сгорания МГД-генератора [101, 146, 147], реагирующего потока в камере сгорания прямоточного воздушнореактивного двигателя [ 148], причем в последнем случае рассмотрено течение предварительно перемешанных метана и воздуха в стехиометрическом соотношении, начинающих реагировать на входе в камеру с расширением, при отношении D/d = 2. Рассмотрено влияние горения на условия образования, размеры и форму рециркуляционных зон при вариации угла наклона торцевой стенки камеры α и угла установки лопаток завихрители φ.
Рис. 4.106. Определенные расчетным путем зависимости длины угловой рециркуляционной зоны от угла наклона торцевой стенки камеры с внезапным расширением а и угла установки лопаток завихрители φ.
Сплошная линия — поток с горением; штриховая — без горения.
Сплошная линия — поток с горением; штриховая — без горения.
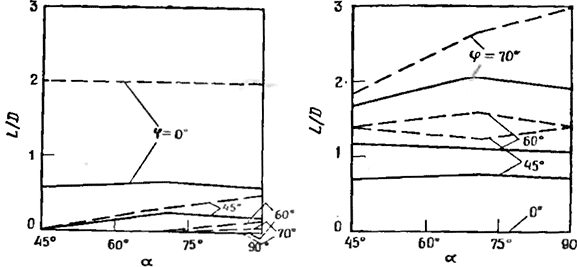
Рис. 4.107. Определенные расчетным путем зависимости длины приосевой р циркуляционной зоны от угла наклона торцевой стенки камеры с внезапно расширением а и угла установки лопаток завихрители φ.
В этих работах использованы стандартная kт—ε-модель турбулентности и комбинированная модель горения с определением скорости химических реакций по закону Аррениуса и по модели распада вихрей. Детали методики изложены в работе [149] и в описании вычислительной программы ЦП).
Анализ большого количества картин линий тока позволь параметризовать характеристики рециркуляционных зон.
На рис. 4.106 и 4.107 показаны расчетные зависимости длины соответственно угловой и приосевой рециркуляционных зон с угла наклона торцевой стенки камеры а и угла установи лопаток завихрители φ в потоках с горением и без горения: истекающих в осесимметричную камеру с отношением D/d.
Наконец, в-четвертых, горение уменьшает длину как угловой, так и приосевой рециркуляционных зон. Укорочение рециркуляционной зоны при горении с повышением скоростей в зоне и уменьшением потока массы, вовлеченной в рециркуляционное движение, отмечалось также авторами работы |133], которые рассчитывали течение в камере с внезапным расширением. Протекание химических реакций, расширение газа и увеличение продольной скорости способствуют укорочению зон, поскольку медленно движущийся газ вблизи нижнего по потоку конца зоны приобретает ускорение, направленное к оси.
Хотя результаты расчетов закрученных реагирующих потоков с рециркуляционными зонами в камерах сгорания качественно и согласуются с экспериментальными данными, количественное соответствие обычно посредственное. Трудности, встретившиеся при моделировании течении с химическими реакциями, потребовали проведения исследований изотермических потоков, направленных на усовершенствование моделей турбулентности с целью лучшего описания процесса смешения. В настоящее время развернуты как экспериментальные, так и теоретические исследования такого рода. Анализируя свои данные и данные других исследователей, авторы работы [142] определили возможную точность моделирования современными методами течений с закруткой и рециркуляционными зонами без химических реакций. Результаты этого анализа схематически представлены на рис. 4.108. Следует отметить, что на качество расчетов очень сильно влияет точность задания параметров на входе в камеру сгорания.
При расчете турбулентного течения с рециркуляционными зонами очень важно также минимизировать схемную вязкость, связанную с представлением конвективных членов разностями против потока. В работе [150] разработана методика оценки ошибки, вызванной схемной вязкостью, и предложен способ уменьшения этой ошибки за счет направленного измельчении сетки. Расчет течения за диском показал, что решение не зависит от сеточных параметров при числе узлов 50 X 55 и на таких сетках можно изучать истинные характеристики моделей турбулентности. Во всех расчетах, проводимых с целью проверки моделей турбулентности, необходимо исключать влияние схемной вязкости. Однако необходимо учитывать то, что в большинстве течений турбулентные напряжения трения по крайней мере на два порядка величины меньше скоростного напора [151] и, следовательно, играют существенную роль только в небольшой части потока, например вблизи точек торможения.

Рис. 4 108. Обобщение данных о точности численного моделирования отдельных областей закрученного течения без химических реакций [142]:
зона 1 — вход в камеру (точность моделирования определяется точностью задания входных профилей параметров);
зона 2 — область рециркуляционных движений (размеры областей рециркуляции занижаются в расчетах на 15... 20%, интенсивность рециркуляционного движения занижается на 20 ... 25 %, профили параметров моделируются качественно);
зона 3 — область течения в пограничном слое, погрешность моделирования не более 10...15 %.
Точность моделирования турбулентности не имеет существенного значения для течений, обусловленных действие] больших градиентов статического давления. Лаундер [152] указал еще одну причину, в силу которой применение моделей типа kT—ε оказывается успешным. В ограниченном потоке пограничном слое происходит интенсивная генерация турбулентности. Масштабы этих турбулентных вихрей малы, чт способствует их быстрой диссипации. Таким образом, отношение скорости генерации к скорости диссипации энергии турбулентности в потоке постоянно, а константа пропорциональном примерно равна единице. Основательное обсуждение и провер ка справедливости такой концепции для течений в камера сгорания проведены в работе [113]
Заканчивая раздел о методах расчета течений с сильно закруткой, уместно указать труды последних конференций [153—159], содержащие много полезной информации. В эти работах приведены результаты расчетов и сопоставление с экспериментальными данными для течений с реакциями и без реакций. Изложены новые подходы в моделировании турбулентности и горения (взаимодействие этих процессов, их влияний на образование загрязняющих веществ), т. е. те проблемы, которые находятся сейчас в центре внимания исследователей
изучающих закрученные течения и занимающихся вопросами их использования в топках, газотурбинных и поршневых двигателях.

