Измерение характеристик турбулентности.
С целью описания турбулентных закрученных течений были проведены подробные измерения средних значений скорости и турбулентных пульсаций с помощью термоанемометра. В работе [21] была исследована одиночная закрученная струя при S = 0,3, использовался термоанемометрический датчик с одним чувствительным элементом. Данные по средним скоростям и пульсационным характеристикам, аналогичные приведенным на рис. 3 23, были получены Чигиром и Червинским. В работе [54] были исследованы струи с S≤0,6; данные по нормальным и сдвиговым напряжениям приведены соответственно на рис. 3.24 и 3.25 для случая максимальной рассмотренной в этой работе закрутки. В этой работе использовались однониточный термоанемометрический датчик и метод измерения при шести положениях датчика.
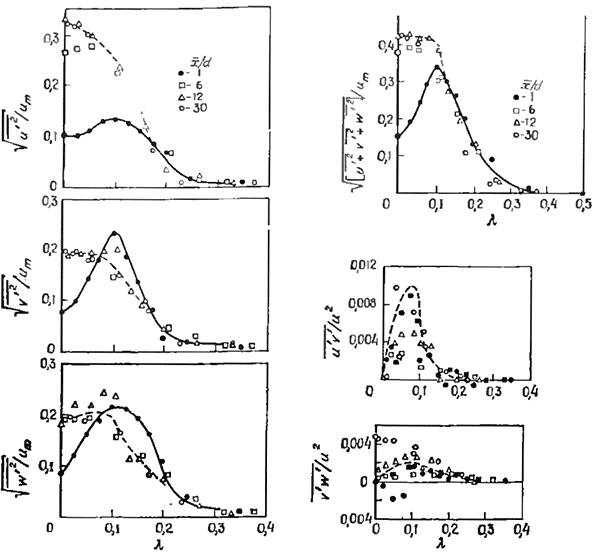
Рис. 3.23. Результаты измерения характеристик турбулентности в слабозакрученной струе при 5 = 0,3 [21].
Позднее была усовершенствована методика обработки сигналов, и измерения указанным методом были проведены в сильнозакрученной струе при S = 2,2 [78]. Сопоставление данных по пульсационным характеристикам и по градиентам средней скорости позволило получить данные по турбулентной вязкости.
В работах [68, 79] описаны результаты недавних измерений с помощью лазерного анемометра в свободных закрученных течениях с горением и без горения. В этих работах были измерены поля скорости и кинетической энергии турбулентности. Результаты измерений показали, что горение приводит к значительному увеличению кинетической энергии турбулентности и амплитуды пульсаций скорости.
Недавно были проведены наиболее полные измерения лазерным анемометром характеристик закрученного ограниченного течения с горением и без горения [80]. Измерения были проведены в модельных топках Имперского колледжа (Лондон) и Харуэлла.
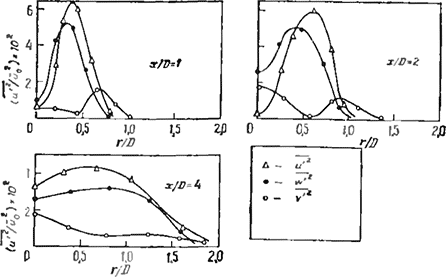
Рис. 3.24. Измерение нормальных компонент турбулентных напряжений в силь- нозакрученной струе прн S = 0.6 [54].
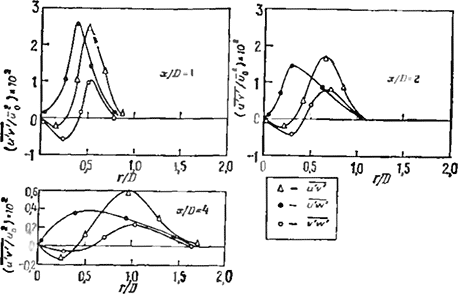
Рис. 3.25. Измеренные компоненты турбулентных сдвиговых напряжений в сильнозакрученной струе при S = 0,6 [54].
В качестве примера на рис. 4.81 приведены изотахи для двух случаев течения: изотермического и с горением. Б каждом случае измерения проводились при двух уровнях закрутки в осесимметричной топке при использовании смеси воздуха и природного газа. Измерения трех компонент средней скорости и соответствующих нормальных напряжений на границах и в поле течения предназначались для оценки методов расчета турбулентных течений, и в связи с этим они более подробны и точны, чем предыдущие исследования в топках, проведенные в Дельфте, Эймёйдене и Карлсруэ. Результаты показали, например, что рециркуляционные зоны в реагирующих потоках значительно отличаются от зон, образующихся в нереагирующих потоках. В большей части поля течения турбулентность значительно отличается от изотропной. Показано также, что в результате горения пульсации скорости существенно возрастают (это проявляется при интегрировании по всему полю течения), что в некотором смысле подтверждает гипотезу о порождении турбулентности горением.
В исследовательском центре фирмы United Technologies (Ист-Хартфорд, шт. Коннектикут) также были предприняты попытки измерения лазерным анемометром характеристик турбулентных закрученных течений с горением [81]. Измерения были проведены в начальной области смешения ограниченного турбулентного диффузионного пламени. Измеренные профили осевой и окружной средних скоростей, распределений среднеквадратичных пульсаций скорости показывают, что происходят существенные изменения осредненного и пульсационного поля течения при изменении давления в камере сгорания и закрутки воздуха на входе. Эти изменения оказывают существенное влияние на эмиссию загрязняющих веществ. Обнаружено значительное увеличение доли крупномасштабных пульсаций в пульсациях скорости. Крупномасштабные пульсации приводят к большим отклонениям от гауссова распределения плотности вероятности турбулентных пульсаций и к значительному отклонению от изотропии в большей части начальной области. Наличие таких крупномасштабных движений указывает на то, что модели турбулентности, основанные на предположениях о локальном равновесии, будут неадекватно описывать эти течения с горением. В работе [81] представлены характерные профили осевой и окружной компонент средней скорости в различных сечениях камеры сгорания при изменении давления и интенсивности закрутки.
Уайтлоу и др. исследовали экспериментально и теоретически струи с закруткой (S = 0,23) и без закрутки (S = 0) в неограниченном [82] и ограниченном [83] потоках. В этих работах представлены лишь данные по полям средней скорости и нормальных напряжений, однако в них содержится полезное обсуждение достоинств и недостатков термоанемометра и лазерного анемометра, проводится их сравнение.
Моделирование турбулентности
Увеличение степени закрутки оказывает значительное влияние на структуру турбулентности: энергию турбулентности на единицу массы Кт, скорость диссипации ε, масштаб l, на нормальные (и'2 и т. д.) и сдвиговые (и'ν' и т. д.) турбулентные напряжения. Это следует учитывать в моделях турбулентности для расчета течений с закруткой. Оказывается, что первичная компонента вязкости μχ,τ значительно возрастает при увеличении интенсивности закрутки и турбулентная вязкость становится неизотропной.
Имеется несколько методов поиска приемлемых моделей турбулентности, позволяющих достичь надежных результатов: экспериментальный, обратный и расчетный. Исследования в этих областях позволили лучше разобраться в структуре турбулентности закрученных течений и дали обоснование необходимости учета анизотропии. В недавних экспериментальных и расчетных работах обсуждались предположения об изотропии для турбулентных закрученных течений. Для проведения моделирования (а следовательно, и расчета) этих течений необходимо модифицировать простые модели турбулентности или разработать более совершенные модели. В данном подразделе приводится обзор и делаются попытки количественной оценки результатов некоторых из этих работ; показывается, как стандартные модели турбулентности 184—90) могут быть распространены на решение задач, связанных с закрученными течениями.
Экспериментальные методы.
С помощью термоанемометров или лазерных анемометров могут быть измерены распределения различных компонент напряжений и средней скорости и, следовательно, градиенты скорости. Такие распределения позволяют определить значения компонент тензора турбулентной вязкости во всех точках поля

Рис. 3.26. Экспериментальные радиальные распределения двух компонент турбулентной вязкости при z/D= 67 для закрученного течения в трубе при угле установки лопаток закручивающего аппарата φ = 55,8°, примерно соответствующем параметру закрутки S = I [91]
течения. Затем можно проверить, соответствует ли определенная модель турбулентности таким распределениям вязкости и напряжений. Этот метод был использован для исследования закрученного течения в трубе [91], свободных закрученных струй [54] и поля течения вблизи рециркуляционной зоны на выходе из закручивающего устройства [78].
В каждом случае турбулентность была такой, что наблюдались значительные изменения компонент тензора турбулентной вязкости в осевом и радиальном направлениях, а также заметная анизотропия. Типичные результаты представлены на рис. 3.26—3.28.
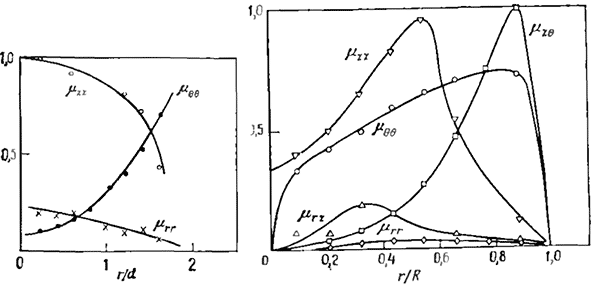
Рис. 3.27. Экспериментальные радиальные распределения трех нормальных компонент турбулентной вязкости μ и μθθ при z/d = 4 для сильнозакрученной струи с параметром закрутки S = 0,6 (кружками и крестиками отмечены экспериментальные значения) [541.
Рис. 3.28. Экспериментальные радиальные распределения пяти компонент турбулентной вязкости (компонента r0 мала по сравнению с остальными и не показана) при z/d = —0,057 для сильнозакрученного течения с параметром закрутки 5 == 2,2 [781.
Обратные методы.
Имея экспериментальные распределения средних значений величин в поле течения, соответствующим дифференцированием и интегрированием дифференциальных уравнений в случае течений типа пограничного слоя можно получить распределения двух компонент тензоров турбулентного напряжения, вязкости и т. п. Могут быть использованы аналитические и численные методы; к достоинствам последних относится возможность обрабатывать любые функциональные формы, для чего имеются общие программы расчетов на ЭВМ. На основе результатов применения этих методов можно выбрать лучшие из моделей турбулентности и дать предложения по их усовершенствованию.
Для нахождения компонент турбулентной вязкости для стационарного закрученного течения в кольцевом канале были использованы [92] полуаналитические обратные методы, и в общем случае было получено σ>1, особенно вблизи внутренней поверхности при высокой интенсивности закрутки.
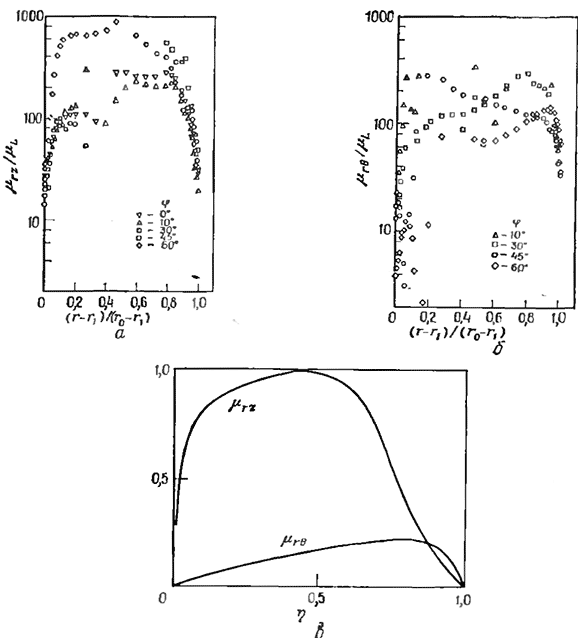
Pис. 3 29. Теоретические обратные расчеты μrz и μr0 для закрученного течения в стационарном кольцевом канале при z/D = 2,5:
а и б—влияние постепенного увеличения угла установки лопаток закручивающего аппарата от 0° до 60°; в — тенденции при фиксированном φ= 60° (S = 1.1) |92|.
На рис. 3.29 представлены результаты вычислений относительных величин двух компонент тензора турбулентной вязкости при различных углах установки лопаток закручивающего аппарата φ от 0° до 60° (рис. 3.29,а и б), а кривые на рис. 3.29, в отражают тенденции изменения этих величин для случая угла установки φ = 60°, что соответствует параметру закрутки
S≈1,1.

Рис 3.30. Численные обратные расчеты двух компонент турбулентной вязкости μ при z/D = 2 для сильнозакрученной струи с параметром закрутки S = 0,6 [94].
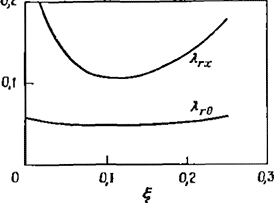
Рис. 3 31. Численные обратные расчеты двух компонент турбулентного пути смешения λ при z/D = 2 для сильнозакрученной струи с параметром закрутки S — 0,6 [94].
Это совпадает с предположениями, основанными на изучении свободных закрученных струйных течений; и действительно, теоретические [93] и численные [94—96] обратные расчеты показывают, что распределение турбулентных напряжений является анизотропным и что μ — функции степени закрутки и координат в поле течения. Численные расчеты показали также, что в случае использования модели пути смешения Прандтля предположение об изотропном однородном распределении параметра пути смешения вполне справедливо при слабой закрутке, но становится все более неприемлемым при увеличении степени закрутки [94].

Радиальные распределения μ и соответствующие значения масштабов λ при x/d = 2 и 15 получены в работе [94].
Рис. 3.32. Теоретические обратные расчеты -компоненты параметра вязкости.
На рис. 3.30 и 3.31 показаны соответствующие тенденции для случая максимальной реализовавшейся закрутки (S=0,6). Эти результаты в общем подтверждают, что σ > 1, особенно вблизи оси или выходного сечения сопла и при более высокой степени закрутки. К примеру, σ уменьшается от величины около 10 вблизи оси примерно до единицы во внешней области слоя смешения при S=0,4 и z/d =6; эта тенденция подтверждается и теоретическим [93) и численным методами [94] и представлена на рис. 3 32, а и б.
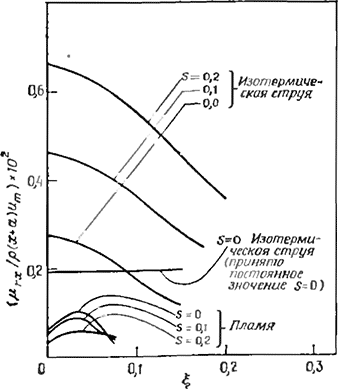
Рис 3.33. Поперечные распределения нормальной компоненты турбулентной вязкости в слабозакрученных струях [95].
При изменении степени закрутки требуется введение изменений в нормализованные значения μrx и эти изменения отличаются в зависимости от наличия или отсутствия пламени. На рис. 3.33 показаны поперечные распределения рассчитанной компоненты тензора турбулентной вязкости в слабозакрученных течениях. Поперечные распределения параметра пути смешения λ в закрученных струях и пламенах приведены на рис. 3. 34.
Расчетные методы.
При использовании модели турбулентности и численных методов расчета прямое решение уравнений дает распределение средних и пульсационных значений актуальных параметров. Если оставить в стороне проблемы численного решения, обсуждающиеся, например, в работе [88], то при введении изменений модели турбулентности можно наблюдать изменения в результатах расчета, а сравнением с экспериментальными значениями средних по времени величин можно наметить пути усовершенствования модели турбулентности. Использование различных моделей для одного и того же течения позволяет выбрать наилучшую из них и определить пригодность или непригодность данной модели для расчета рассматриваемого течения.

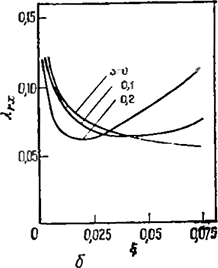
Рис. 3.34. Поперечные распределения значений пути смешения в закрученных струях и пламенах [95]: а — струн; б — пламена
В этом направлении были проведены многочисленные исследования Расчеты подтвердили или позволили отбросить некоторые возможные изменения моделей турбулентности. В случае модели пути смешения Прандтля были предложены различные модификации для случая слабозакрученных течений; задача состояла в том, чтобы связать rθ-компоненту сдвигового напряжения с rх-компонентой тензора вязкости в уравнении для осевого направления и учесть анизотропию вязкости. Первая задача обычно решается введением пропорциональной зависимости rx-компоненты тензора вязкости от второго инварианта тензора скорости деформации осредненного течения и последующего использования переменного параметра r-компоненты вязкости. Было предложено следующее выражение:
![]()
вместе с соотношениями
![]()
σrх и т. д. —постоянные, зависящие от S, или переменные, зависящие от S. В осесимметричном случае в цилиндрических координатах имеем![]()
что в приближении пограничного слоя сводится к выражению
![]()
Известная модель Прандтля для незакрученного течения является частным случаем этого выражения. Заметим, что модели этого типа удовлетворяют требованию о том, что μ сводится к обычной модели Прандтля для незакрученных течений при стремлении w к нулю. В частности, при Sx →0 с увеличением расстояния вдоль оси (для затопленной закрученной струи) λ стремится к принятому для незакрученного течения значению 0,08. Коэффициент (1 + λS) учитывает изменение масштаба длины вследствие закрутки, что дает более высокие значения rx-компоненты тензора вязкости в результате движения закрутки, как описано в гл. 2 [32]. Это аналогично формуле Монина — Обухова, которая была предложена как средство простой аппроксимации зависимости пути смешения οι кривизны линий тока и от центростремительных ускорений [98).
Были рекомендованы параметры
![]()
что соответствует некоторой степени анизотропии и дает хорошие результаты, которые получаются при использовании приведенного выше подхода [97]. Основное влияние анизотропии проявляется вблизи выходного сечения; и действительно, при проведении расчета слабозакрученных струй, начиная с сечения x/d — 2, с использованием изотропной модели следующего вида [99]:
![]()
получаются результаты, удовлетворительно согласующиеся с экспериментальными данными по дальнейшему развитию потока. В работе [100] также сделано предположение об изотропии, но при этом включена поправка к μ на влияние закрутки и как следствие получены хорошие результаты для рассмотренной системы.
Слабозакрученные течения оказались также полезным испытательным объектом для других моделей турбулентности. В случае моделей типа энергия — масштаб влияние закрутки часто учитывается введением дополнительного слагаемого типа источника в уравнение для k и (или) для Z. Аналогично Ротта и Роди уравнение для Z в виде Z = kl было использовано в работах [101] и [97] для расчета слабозакрученных течений, причем влияние закрутки описывалось дополнительным источниковым членом CRρRik1,5 в уравнении для Z. Было показано, что использование выражений
![]()
позволяет рассчитывать свободные закрученные струи вплоть до образования рециркуляционных зон [97]. Числа Шмидта для ft и Z брались равными единице.
Результаты расчета свободной слабозакрученной струи хорошо согласуются с экспериментальными данными по осредненным и пульсационным характеристикам (рис. 3.35). Расчет дает анизотропию при использовании этой модели (если вводятся компоненты вязкости, но в этом нет необходимости), и на рис. 3.36, а видно, что максимальное значение σθ = 3 на оси при x/d = 6 и это максимальное значение быстро уменьшается с расстоянием вниз по потоку. Осредненные по радиусу значения σθ примерно такие же, как полученные в результате численного анализа [97] с целью удовлетворительного расчета средних значений при использовании более простой модели турбулентности (использующей постоянное значение σrθ в каждом сечении потока), но несколько меньше, чем полученные обратными методами [93, 94] на основе средних по времени значений.
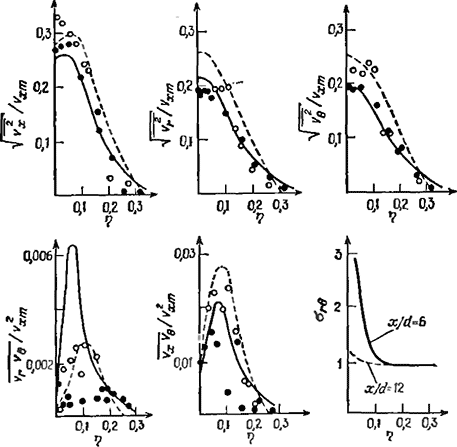
Рис. 3.35. Результаты расчета компонент нормального и сдвигового напряжений [90] и сравнение с экспериментальными данными [21] для закрученной струн при S= 0,3. Сплошные расчетные кривые и темные экспериментальные точки соответствуют значению x/d = 6, штриховые расчетные кривые и светлые экспериментальные точки соответствуют x/d =12.

Рис. 3.36 Результаты расчета параметра вязкости, характеризующего анизотропию:
а — Свободной слабозакрученной струи (S = 0,3) (I) с использованием алгебраической модели турбулентных напряжений; б — дли свободного вращающегося диска с использованием соотношений для напряжения и с использованием модели пути смешения с пристеночными соотношениями (III); в—для цилиндра, вращающегося в однородном потоке в направлений оси с использованием алгебраической модели турбулентных напряжений (IV) [106]
На рис. 3.36,б и в приведены результаты расчета, характеризующие анизотропию рассматриваемых характеристик для течения около свободного вращающегося диска и для цилиндра, вращающегося в однородном потоке в направлении оси цилиндра. Следует отметить, что значения σrθ близки к единице во внешней части пограничного слоя, где число Рейнольдса, определенное по параметрам турбулентности, велико, но значительно уменьшаются вплоть до значений около 0,25 в области пристеночного подслоя [106].
Для расчетов более сильно закрученных течений в камерах сгорания были использованы менее сложные модели турбулентности, хотя в этих течениях требуется описание всех шести компонент напряжений или вязкости. В целом хорошие результаты расчета получились в работе [102] при использовании модифицированной модели пути смешения, в работах [103] и [104] с использованием для σrθ значений от 5 до 10 с подбором в каждом конкретном случае и в работе [105] с использованием значения σrθ, достигающего 30. Однако эти сильнозакрученные течения служат лишь для апробации модели турбулентности. Для расчета закрученных течений используются вполне правдоподобные усовершенствованные варианты более элементарных моделей, и эти усовершенствованные модели дают лучшее общее согласование с экспериментом, чем немодифицированные стандартные модели.
Параметр анизотропии σ особенно важен, в частности, и для слабозакрученных течений, поскольку было обнаружено, что он а) превышает единицу и возрастает с увеличением параметра закрутки при приближении к оси и к выходному сечению в случае закрученных струйных течений, и б) не превышает единицы в области пристеночного подслоя в случае более сильно меняющегося в радиальном направлении течения около вращающегося конуса или диска. Общие эффекты смешения можно учесть простыми изменениями элементарных моделей турбулентности, но для тех исследователей, которые хотят добиться более подробного моделирования, особенно в случае сильно закрученных течений, рекомендуется использовать новые идеи по дифференциальному или алгебраическому моделированию напряжений.

