КОДИРОВАНИЕ ИНФОРМАЦИИ. КОДИРУЮЩИЕ И ДЕКОДИРУЮЩИЕ УСТРОЙСТВА
Основные сведения и понятия теории кодирования
Под кодированием в общем случае понимают процесс преобразования сообщения в сигнал.
Код - это совокупность правил, по которым сообщение преобразуется в сигнал. Различают две группы правил: 1) правила образования кодовых слов и 2) правила сопоставления кодовых слов кодируемым сообщениям.
Кодовое слово - это упорядоченная последовательность элементов, составленная по правилам образования кодовых слов рассматриваемого кода и несущая информацию одного сообщения.
Упорядоченную последовательность символов (знаков), отображающую кодовое слово, называют кодовой комбинацией или комбинацией кода.
Комбинации, которые можно составить по правилам данного кода, принято называть разрешёнными, а любые другие комбинации, составленные из тех же элементов, но не удовлетворяющие правилам кода, называют запрещёнными.
Замечание. Не следует употреблять вольные выражения типа «в линию связи передаётся код», «из линии (канала) связи принимается код» и тому подобные. Поскольку ни «передать», ни «принять» код нельзя - можно передавать и принимать только сигналы.
Обычно в системах передачи информации каждое сообщение вначале преобразуется в первичный дискретный сигнал, а затем первичные сигналы кодируются. В таком случае кодирование понимается в более узком смысле этого слова - как получение дискретного сигнала определённой структуры, удовлетворяющего заданным требованиям к верности и помехоустойчивости передачи информации. Сигналы, полученные процедурами кодирования, называют кодированными. Кодированные сигналы способны противостоять действию помех, и поэт ому их можно передавать на большие расстояния.
Структура закодированного сигнала определяется правилами первой группы (см. выше) и, в общем случае, зависит от свойств выбранного кода и также от характера передаваемых сообщений.
Обратные кодированию процедуры, в результате которых «восстанавливается» сообщение из кодированного сигнала, называются процедурами декодирования, а сам процесс реализации этих процедур - декодированием. Как правило, декодирование заключается в получении первичного сигнала, соответствующего переданному сообщению.
В зависимости от свойств выбранного кода при декодировании принятых сигналов возникающие от помех ошибки могут быть обнаружены и даже исправлены. Поэтому существует возможность отказа от реализации принятого сообщения (в случае только обнаружения ошибок) или, несмотря на действие помех, правильно реализовать сообщение (в случае исправления ошибок). Поэтому-то кодированием можно увеличить помехоустойчивость и верность передачи информации, что является одной из основных целей кодирования.
Другой важной целью кодирования является обеспечение наибольшей эффективности передачи информации. Обычно под эффективностью понимают передачу заданного количества информации с наибольшей скоростью при заданных требованиях к верности и помехоустойчивост и передачи. Путём кодирования сообщений большой длины кодовыми словами малой длины можно сократить время передачи сигналов и тем самым обеспечить наибольшую скорость передачи информации, т. е. повысить эффективность передачи.
С другой стороны, кодирование можно рассматривать как один из методов «сжатия» сообщений. В результате образуется сообщение меньшей длины, но содержащее то же количество информации, что и исходное сообщение. В частности, это учитывается второй группой правил кодообразования. Согласно этим правилам необходимо каждое кодовое слово однозначно сопоставить кодируемому сообщению. Существуют два варианта сопоставления.
Первый — любому из множества кодируемых сообщений ставится в соответствие одно (любое) из множества разрешённых кодовых слов.
Второй - на сопоставление влияет вероятность появления кодируемого сообщения, а именно: сообщению с наибольшей вероятностью соответствует кодовое слово наименьшей длины, а сообщению с меньшей вероятностью - кодовое слово большей длины. Это так называемое статистическое кодирование информации.
Первый вариант сопоставления правомочен, когда все кодируемые сообщения равновероятны. При этом разрешённые кодовые слова приобретают одинаковую длину и коды называют равнодоступными, или комплектными.
Во втором варианте кодовые слова формируются разной длины. В этом случае коды называют статистическими. Применение статистического кодирования будет оправданным, если кодируемые сообщения появляются с различными вероятностями. Так при передаче телеметрической информации, когда измеряемые величины поддерживаются неизменными на уровне своих номинальных значений, сообщения о номинальных значениях возникают с большей вероятностью, а сообщения об отклонении от номинальных значений возникают с меньшей вероятностью. Статистическое кодирование позволяет увеличить среднюю скорость передачи информации приблизительно на 25%.
Подводя итог сказанному, следует отметить:
- Требования к обеспечению наибольшей верности и высокой эффективности передачи информации противоречивы. Методы достижения наибольшей верности (и помехоустойчивости) приводят к уменьшению эффективности передачи и, наоборот, методы увеличения эффективности ведут к снижению помехоустойчивости (и верности) передачи. Поэтому возникает проблема выбора кода, обеспечивающего заданную верность при некоторой оптимальной эффективности передачи информации.
- Кодирование позволяет не только обеспечить необходимые требова ния к верности, помехоустойчивости и эффективности передачи информации, но и в ряде случаев обеспечить секретность информации - защиту от несанкционированного доступа к ней.
- Существует множество кодов, различающихся как наименованием, так и свойствами по части обнаружения, исправления ошибок и областью применения (в зависимости от вида кодируемой информации).
Основные параметры и характеристики кодов
Обычно под «параметром» понимают количественную оценку некоторой физической величины либо зависимости (функции), вводимую в конкретных обстоятельствах для сравнительной оценки величин и функций. Применительно к кодам, определяемым как совокупность правил, параметрами являются:
- Длина кодовых комбинаций (кодовых слов) - n, численно равная общему числу элементов, из которых формируются комбинации. Длине (n) кодовых слов однозначно соответствует число элементов закодированного сигнала.
- Основание кода (или алфавит кода) - т, определяемое как полное множество значений, которые может иметь (принимать) элемент кода. Основанию кода (m) однозначно соответствует число значений качественных признаков, используемых для формирования сигналов (см. раздел 2 настоящего пособия).
К основным характеристикам кода относят:
- Мощность кода — Ν, определяемая как полное множество (число) комбинаций, которые можно составить по правилам рассматриваемого кода. Мощность кода зависит от длины кодовых комбинаций и основания кода. Другими словами, мощность кода - это максимальное число разрешённых комбинаций данного кода. Мощность предопределяет количество информации (и размерность массива информации), которое можно закодировать и передать выбранным кодом.
- Избыточность кода — D, она показывает, какая часть элементов кодовых слов (комбинаций) не участвует в передаче информации, а служит лишь целям её "защиты" от помех. Избыточность определяется выражением
![]() (1)
(1)
где η - длина кодовых комбинаций рассматриваемого кода; n0 — число информационных элементов этого кода: к - число контрольных (проверочных) элементов, не участвующих в передаче информации.
Коды могут быть избыточными (к ≠ 0) и безызбыточными (к = 0) и соответственно D - 0. В безызбыточных кодах все элементы являются информационными, поэтому искажение под действием помех информационного элемента приведет к искажению информации и, как следствие, к возможности трансформации передаваемого сообщения.
Минимальное кодовое расстояние или расстояние Хэмминга - d.
Минимальное кодовое расстояние — это число минимальных отличий двух любых разрешённых комбинаций рассматриваемого кода при их поэлементном сравнении и полном попарном переборе всех комбинаций. Понятие «кодовое расстояние» используется при геометрическом отображении полного множества разрешённых комбинаций некоторого кода в виде гиперкубов, когда код представляется геометрической моделью. Вершины гиперкуба соответствуют конкретным кодовым комбинациям, а соединяющие две соседние вершины куба рёбра показывают расстояние (переходы) между выбранными комбинациями. Размерность гиперкуба определяется числом элементов и основанием рассматриваемого кода. Рис. 3.1,а представляет собой геометрическую модель двухэлементного двоичного кода. Соседние вершины этого двоичного двумерного куба расположены по концам рёбер, т.е. на расстоянии одного перехода (d=l). Комбинации же, расположенные по диагоналям (01, 10 и 00, 11), находятся на расстоянии двух кодовых переходов (d=2). Если в качестве разрешённых комбинаций выбрать 10 и 01 либо 00 и 11, то получим коды с минимальным расстоянием два (d = 2).
По геометрической модели троичного 2-элементного кода (рис. 3.1,б) можно выбрать комбинации кода с минимальным расстоянием d = 2. Например, это комбинации, образующие подмножество {22, 00,12, 21, 11}. Правда, в указанном подмножестве комбинаций есть комбинации, находящиеся на расстоянии четырёх кодовых переходов, например комбинации 22, 11 либо комбинации 12 и 21. Однако для заданного этим подмножеством кода минимальное расстояние равно двум. По геометрическим моделям 3-элсментных кодов (см. рис.3.1,в и г) можно отыскать комбинации, находящиеся на расстоянии 3-х кодовых переходов, например 100 и 011 (рис. 3.1,е), и даже на расстоянии шести кодовых переходах, например 211 и 122.
Расстояние Хэмминга предопределяет свойства кода в отношении возможностей обнаружения и исправления ошибок, т.е. оно позволяет определить, сколько ошибок можно обнаружить, а сколько ошибок можно исправить при декодировании. Минимальное кодовое расстояние d можно рассчитать по формуле
![]() (2) где s - число исправляемых ошибок; г - число обнаруживаемых ошибок
(2) где s - число исправляемых ошибок; г - число обнаруживаемых ошибок
Из формулы (2) следует, если код не позволяет ни обнаруживать, ни исправлять ни одной ошибки, то минимальное кодовое расстояние равно единице. А чтобы исправить одиночную ошибку, требуется код с минимальным расстоянием d = 3.
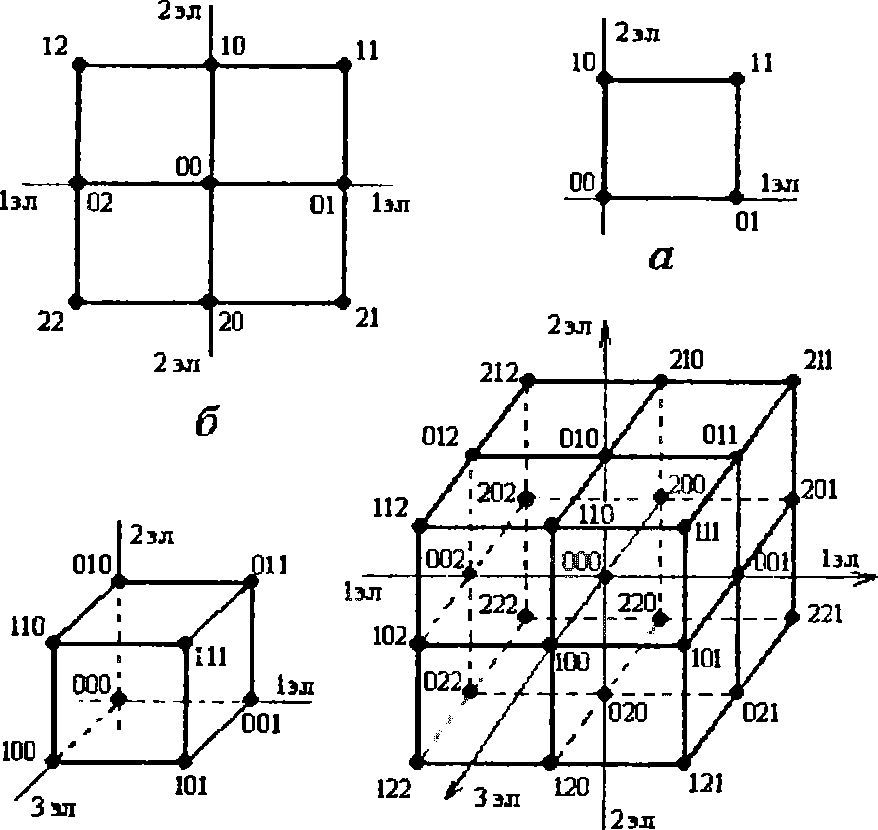
Рис. 3.1. Геометрические модели безызбыточных кодов: 2 - элементных двоичного (а) и троичного (б); 3 - элементных двоичного (в) и троичного (г)

