Одним из важнейших вопросов теории информации является установление меры количества и качества информации. Различают при направления в теории информации:
- структурную теорию, рассматривающую дискретное строение массивов информации и их «измерение» простым подсчётом информационных элементов (квантов);
- статистическую теорию, оперирующую понятием энтропии как меры неопределённости, учитывающей вероятность появления (и информативность) тех или иных сообщении;
- семантическую теорию, которая призвана дать (сформировать) оценки полезности, существенности и ценности информации.
Структурная теория применяется для оценки возможностей аппаратуры информационных систем (запоминающих, регистрирующих и других устройств обработки информации и каналообразующей аппаратуры) вне зависимости от условий их применения.
Статистическая теория даёт количественные оценки информационных систем в конкретных применениях, например, при передаче информации в условиях помех и без помех.
Семантическая теория должна дать оценки эффективности проводимых экспериментов и логических опытов. Она разработана пока недостаточно.
Наиболее развита статистическая (количественная) теория, результаты которой широко используются для сравнительной оценки различных систем и каналов связи.
1.3. Преобразование непрерывных сигналов в дискретные
При передаче непрерывных сообщений, например телеметрической информации, первичный аналоговый сигнал может принимать бесконечное множество значений в ограниченном диапазоне. Непосредственная передача таких сигналов сопряжена с появлением некоторых недостатков у систем передачи информации. В частности, требуется выделенный канал связи или выделенная (не занятая) линия связи, кроме того, возникают трудности с обработкой такой информации средствами вычислительной и компьютерной техники. Поэтому непрерывные сигналы преобразуют в сигналы дискретные как по уровню, так и по времени.
Существуют два основных способа преобразования:
- дискретизацией непрерывного сигнала во времени;
- квантование непрерывного сигнала но уровню.
В результате первого преобразования образуется сигнал непрерывный по уровню, но дискретный во времени, а результатом второго преобразования является сигнал дискретный по уровню, но непрерывный во времени. Это сигналы промежуточных форм, которые затем достаточно просто преобразуются в дискретные сигналы (как по уровню, так и по времени).
Первый способ основан на результатах теоремы В.А. Котельникова, известной в отечественной технической литературе под его именем (Россия. 1933г.). Котельников В.Л. рассмотрел наиболее распространённый случай.
когда сигналы имеют ограниченный частотный спектр и непрерывны во времени. Этот случай справедлив для большинства реальных аналоговых сигналов. отображающих значения физических величин, например результаты их измерений, и сигналов традиционной телефонной связи. Теорема Котельникова формулируется следующим образом:
«Если некоторая функция U(t) непрерывна во времени и имеет непрерывный комплексный спектр Фурье, ограниченный полосой частот 0...Fс, то она может быть полностью представлена совокупностью дискретных отсчётов, взятых через интервал времени
(19) где Fс - частота среза её спектра».
Процесс дискретизации согласно теореме Котельникова иллюстрируется временными диаграммами, приведёнными на рис. 1.3. Непрерывный сигнал отображён графиком U(t), а сигнал, полученный в результате дискретизации - последовательностью импульсов с длительностью
и амплитудами, равными отсчётам функции в соответствующие моменты времени. Диаграммы соответствуют случаю, когда непрерывный сигнал не меняет полярность. В принципе возможны знакопеременные непрерывные сигналы.
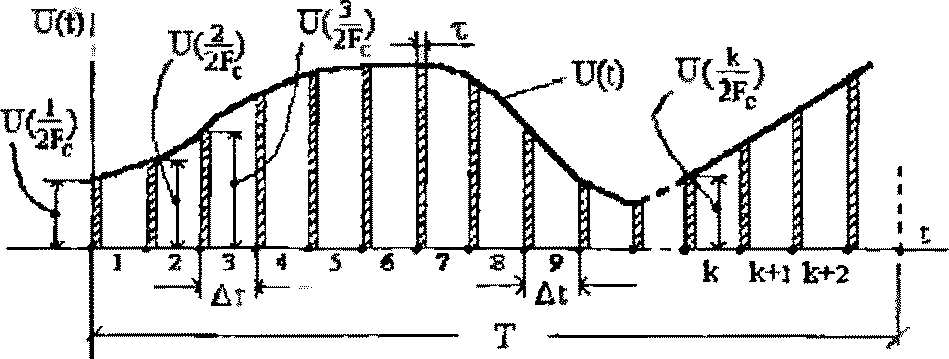
Рис. 1.3. Дискретизация непрерывного сигнала во времени
Действия, вытекающие из теоремы Котельникова, иллюстрируются функциональной схемой (рис. 1.4). Преобразуемый аналоговый сигнал U(t) подаётся на вход аналогового ключа DA1, управляемого (по цифровому входу) генератором тактовых импульсов DD. Частота следования и длительность тактовых импульсов выбираются в соответствии с теоремой Котельникова 
. Затем полученные импульсы усиливаются и по линии связи передаются на приёмный пункт. На приёмном пункте импульсы вновь усиливаются и поступают на вход идеального фильтра низких частот DA4 (показан активный фильтр). На выходе фильтра будет вновь получен аналоговый сигнал
. отличающийся от переданного сигнала U(t) только амплитудой.
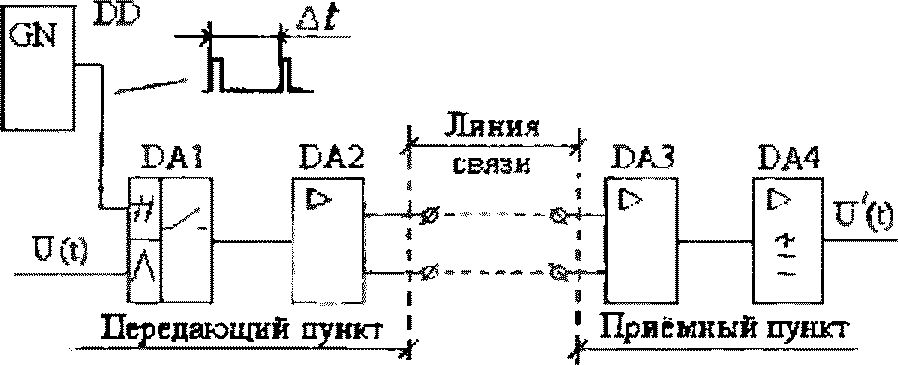
Рис. 1.4 Преобразование непрерывных сигналов в дискретные дискретизацией во времени
Согласно теореме Котельникова В.А. передача будет осуществляться без погрешностей (функция полностью определена), в этом - достоинство рассмотренного способа преобразования. Непосредственное применение этот способ нашёл в телеметрических системах с амплитудно-импульсной модуляцией (см. раздел 4).
Практически возникает погрешность в передаче из-за рассеяния мощности импульсов и неидеальности частотной характеристики фильтра DA4 Стремление повысить помехоустойчивость передачи за счёт кодирования приводит к усложнению кодирующих и декодирующих устройств, так как число значений амплитуд импульсов стремится к «бесконечности». Следовательно, длина кодовых комбинаций будет большой и время передачи увеличится.
Поэтому шаг дискретизации Δt рассчитывают с поправкой η, учитывающей требования к точности воспроизведения передаваемых непрерывных сигналов,
(21)
где δ - допустимая относительная погрешность. Обычно шаг Δt выбирают несколько (в 1,2...2 раза) меньше в сравнении с расчётным значением (19), то есть частоту дискретизации несколько завышают.
Например, при передаче сигналов телефонной связи (традиционной связи - не цифровой) требуется полоса частот в диапазоне (0,3..3,4)кГц. Тогда качество речи вполне приемлемое. Переходя к цифровой связи, требуется выбрать частоту дискретизации равную 6,8 кГц (Fмакс=3,4 кГц). Стандартами МККТТ установлена частота 8 кГц, т.е. больше примерно в 1,2 раза.
В зарубежной литературе результаты, вытекающие из теоремы В.А. Котельникова, и сама теорема известны под именем теоремы X. Найквиста или «теоремы отсчётов».
Найквист X. и Котельников В.А. независимо друг от друга и при разных исходных предположениях получили практически одинаковые результаты.
Первый - для теории систем автоматического управления, а второй — для систем связи.
Преобразование непрерывных сигналов в дискретные можно выполнить другим способом, лишенным недостатков преобразования путём дискретизации сигналов во времени.
