Как уже было сказано выше, эти коды относятся к избыточным кодам, т.е. кроме информационных элементов в кодовых комбинациях есть контрольные (проверочные) элементы, не участвующие в передаче информации и служащие только целям обнаружения ошибок.
Основной проверкой, которая положена в основу формирования контрольных элементов в комбинациях систематических двоичных кодов, служит проверка на четность/нечетность (по единицам) выбранной группы информационных элементов. Логически такие проверки описываются суммой по mod 2 выбранных информационных элементов. Поскольку проверка на нечётность эквивалентна инверсии суммы по модулю два (mod 2), коды группы «чёт» обладают такими же свойствами, что и коды группы «нечет», т.е. коды «чёт» и коды «нечёт» обладают равными возможностями в части обнаружения ошибок, поэтому иногда такие коды называют кодами «с защитой по паритету».
Чтобы код допускал возможность обнаружения хотя бы одной ошибки, необходимо выбрать минимальное кодовое расстояние не менее двух (d > 2). Самым простым является код с одной проверкой на чётность по всем информационным элементам.
Коды с защитой по паритету (коды «чёт/нечёт»)
Самым простым способом поиска множества разрешённых комбинаций таких кодов является полный перебор всего множества комбинаций безызбыточного двоичного η-элементного кода и выбор таких комбинаций, которые содержали бы чётное (нечётное) число единиц. Таких комбинаций будет ровно половина всего множества комбинаций. Поэтому мощность кодов чёт/нечёт можно рассчитать по формуле
(9) где η - длина кодовых комбинаций рассматриваемого кода. В правой части выражения (8) показатель степени (п-1) можно рассматривать как число информационных элементов. Таким образом, число информационных элементов (n0) в любом коде чет/нечет можно определить по формуле
(10)
Иными словами, в комбинациях рассматриваемых кодов будет всегда один контрольный элемент.
Процедуры кодирования сводятся к следующему:
- строится таблица кодирования сообщений простым безызбыточным двоичным кодом с числом информационных элементов n0;
- в полученной по п.1 таблицу добавляется одна позиция для контрольного элемента, и ему придаются значения по признаку чётности (либо нечётности) единиц на информационных позициях.
Местоположение (номер позиции) контрольного элемента не имеет существенного значения. Однако условимся записывать контрольный элемент на первой справа позиции после информационных позиций.
Рассмотрим пример построения кода группы «чёт» для кодирования восьми сообщений (М=8). Процедуры кодирования оформляем табл. 5.
Таблица 5
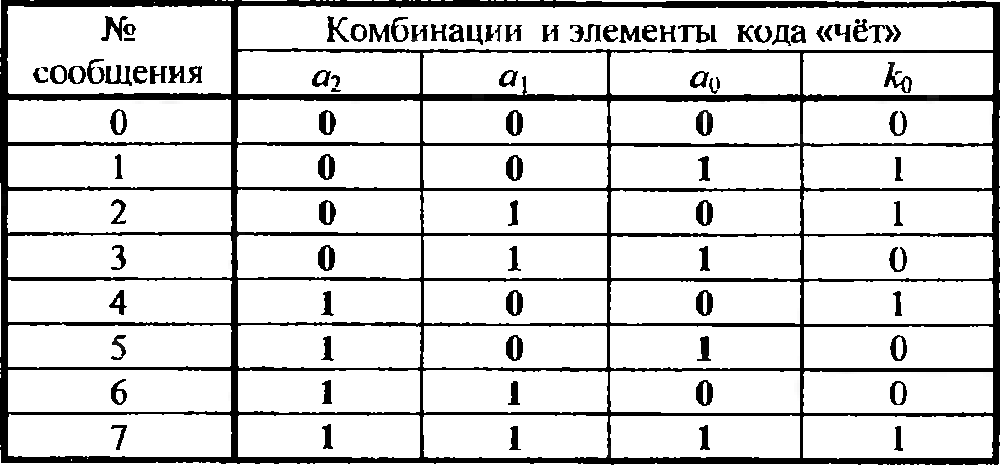
Рис. 3.5. Функциональная схема шифратора
Правый столбец табл 5 отведён под контрольный элемент к0. Значения его выбраны таким образом, чтобы в каждой строке было чётное число единиц. Для рассмотренного примера нетрудно построить кодовый шифратор кода «чёт», дополнив шифратор двоичного безызбыточного 3-элементного кода схемой контроля чётности/нечётности (см. рис. 3.5).
Известно, если некоторое логическое (булево) выражение сложить по mod 2 с логической единицей, то получится инверсия этого выражения. Поэтому в схеме рис. 3.5 предусмотрен ключ (тумблер) SA1, который на четвёртый вход элемента D2 подключает либо сигнал лог.0, либо сигнал лог.1. Положения тумблера SA1 промаркированы названиями кодов, которыми будут кодироваться входные сигналы х0, х1, ...х7.
По обозначению шифратора D1 следует, что активным значением его входных и выходных сигналов является уровень лог.1.
Обратитесь ещё раз к табл. 5. Сравнивая между собой попарно комбинации, нетрудно убедиться, что минимальное кодовое расстояние для этого кода равно двум (d=2). Такой код способен обнаружить только одну одиночную ошибку.
Правила декодирования кодов «чёт/нечёг» аналогичны правилам декодирования простых двоичных кодов. Отличие заключается в том, что, в зависимости от результата проверок на четность/нечётность, будет наложен запрет либо дано разрешение на выдачу результата декодирования. Естественно, что в названных проверках участвуют как информационные, так и контрольные элементы принимаемых комбинаций.
Наиболее экономичными (по аппаратурным затратам) будут дешифраторы, в которых результат декодирования определяется по декодированию комбинации только информационных элементов. Для этой цели требуется стробируемый полный декодер n0-го порядка и схема проверки принятой комбинации на чётность/ нечётность. Выходной сигнал этой схемы необходимо использовать в качестве сигнала разрешения / запрета для декодера. Логическое выражение проверок на чётность для рассматриваемого кода имеет следующий вид
(11) а на нечётность
(12).
В формулах (11) и (12) логическим переменным а2, а1, а0 и к0 соответствуют информационные элементы и соответственно контрольный элемент принятой комбинации.
На рис. 3.6 приведена функциональная схема для декодирования рассматриваемого 4-элементного кода «чет/нечет». В качестве декодера третьего порядка D2 выбрана микросхема К155ИД4. Функцию схемы контроля чётности/ нечётности выполняет 5-входовой элемент D1, являющийся сумматором по mod 2. На его пятый вход подаётся внешний сигнал, принимающий два фиксированных значения. Если декодируется код «чёт», то на этот вход подаётся сигнал лог.0. Для декодирования кода «нечет» следует подать сигнал логической единицы (лог.1). Естественно, что при одиночной ошибке в принятой комбинации чётность единиц будет нарушена, и на выходе элемента D1 возникнет сигнал лог.1.
Поскольку стробирующие входы E1 и Е2 инверсные, то сигнал лог.1 запретит декодирование комбинации информационных элементов. Кроме того, так как сумма по mod2 принимает значение лог. 1 при нечётном числе единиц, т.е. при нечётном числе ошибок в принятой комбинации, то рассматриваемые коды способны обнаружить нечётное число ошибок. Это при условии, что результат декодирования будет зафиксирован (снят) после того, как все элементы кодовой комбинации будут приняты. Если же элементы комбинации поступают последовательно во времени, то при двух и, вообще, чётном числе ошибок передаваемое сообщение будет трансформировано.
Рис. 3.6. Функциональная схема дешифратора кода «чет/нечет»
