Идея получения комбинаций корреляционного кода основана на повторной передаче кодовой комбинации некоторого кода, называемого основным кодом.
Таким образом, мощность корреляционного кода равна мощности основного кода. В качестве основного кода можно выбрать любой двоичный код, т.е. код с любым минимальным кодовым расстоянием, и в том числе двоичный безызбыточный код. Рассмотрим, каким образом формируются комбинации корреляционного кода (процедура кодирования).
Допустим, что в качестве основного выбран двоичный 4-элементный безызбыточный код. Вот его две комбинации: №1 => 1001 и №2 => 1011. Для образования комбинаций корреляционного кода каждый элемент основной комбинации отображается двумя элементами, расположенными на «рабочей» и «контрольной» позициях соответственно. На рис. 3.10 показана схема формирования комбинаций корреляционного кода, соответствующих выбранным комбинациям основного кода.
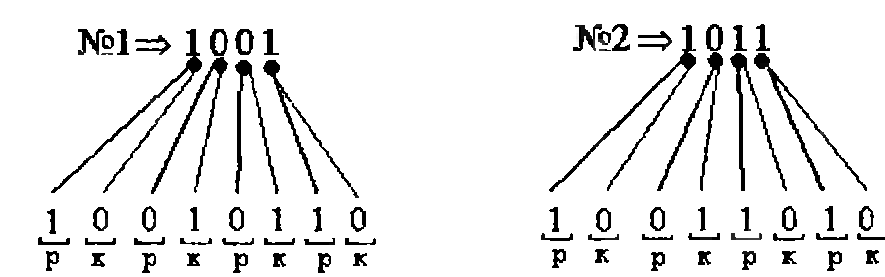
Рис. 3.10. Образование комбинаций корреляционного кода
Как видно по схеме, комбинация на контрольных позициях (помечены буквами «к») является инверсной комбинации на рабочих позициях, помеченных буквой р. Комбинация же на рабочих позициях совпадает с комбинацией основного кода. Если выбранные комбинации №1 и №2 отличаются значением одного элемента, т.е. находятся на расстоянии одного кодового перехода, то полученные комбинации корреляционного кода отличаются уже значениями двух элементов, т.е. минимальное кодовое расстояние равно двум кодовым переходам. Кроме того, комбинации корреляционного кода имеют вдвое больше элементов по сравнению с комбинациями основного кода.
Так как минимальное кодовое расстояние корреляционного кода увеличивается вдвое относительно минимального кодового расстояния основного кода, то корреляционный код приобретает новые свойства в части обнаружения и исправления ошибок.
В частности, корреляционный код с минимальным расстоянием d = 6, состоящий из 12 элементов и полученный двукратной передачей комбинаций кода Хэмминга с d = 3, позволит исправить двойные ошибки и обнаружить три ошибки. Такой вывод вполне согласуется с тем, что при однократной передаче можно исправить одну ошибку, а две ошибки трансформируют передаваемое сообщение.
Кодирующее устройство для такого корреляционного кода можно получить, добавив по каждому выходу схемы (рис. 3.9) элементы НЕ (всего 6 элементов).
Декодирование корреляционных кодов заключается в выполнении следующих процедур; 1) декодирование комбинаций основного кода; 2) со поставление результата декодирования комбинаций на рабочих позициях с результатом декодирования комбинации на контрольных позициях; 3) принятие решения «разрешение/запрег» на выдачу результата декодирования.
Декодирование комбинаций основного кода ведётся по правилам этого же кода. Процедуры сопоставления результатов декодирования комбинаций на рабочих и контрольных позициях можно описать логической операцией: сумма по mod 2 сигналов с одноимённых выходов основных дешифраторов первого и второго декодирующих устройств. В таком случае защитный отказ от выдачи окончательного результата декодирования возникнет только тогда, когда первое и второе декодирующие устройства выдадут «противоречивые» результаты. Это произойдёт при трёх ошибках (две ошибки в комбинации на рабочих позициях и одна ошибка в комбинации на контрольных позициях).
Корреляционные коды позволяют обнаруживать все ошибки, которые приводят к появлению одинаковых значений элементов на рабочих и «спаренных» с ними контрольных позициях. В таком варианте корреляционные коды используются только для обнаружения ошибок. Максимальная кратность обнаруживаемых ошибок для рассматриваемого корреляционного кода на основе кода Хэмминга с d=3 будет равна шести.
В зарубежной литературе по вопросам передачи информации часто употребляются названия кодов такие, как «NRZ-код», «RZ-код», «код Манчестер» и другие.
Эти названия обусловлены правилами формирования уже закодированных сигналов для их передачи по линиям с временным разделением каналов связи. Именно этот способ разделения каналов используется для повторной (многократной) передачи сигналов. При временном разделении каждый элемент кодовой комбинации (и соответствующий элемент сигнала) передастся на определённой (фиксированной) временной позиции. Длительность временной позиции задаётся генератором тактовой частоты, определяющей скорость передачи информации. Период следования тактовых импульсов (At), как правило, остаётся постоянным и предопределяет длительность одной временной позиции.
Названные коды различаются тем, как используется временная позиция, отведённая для передачи одного элемента (и одного бита информации) кодовых слов. Проиллюстрируем это различие временными диаграммами сигналов, закодированных кодом Хэмминга с d=4, при передаче, например, комбинации 6 (см. табл. 8). Эти диаграммы приведены на рис. 3.11.
Как видно из диаграмм, отличия кодов NRZ и RZ состоят в том, что у кода NRZ элемент кодовой комбинации с признаком «1» передаётся сигналом лог.1 в течение всего такта длительностью At, а у кода RZ в течение полтакта. Таким образом, сигнал передаваемый «кодом» RZ, представляет собой последовательность импульсов, разделённых паузами. При коде же NRZ длительность сигнала лог. 1 может быть произвольной, но кратной длительности такта.
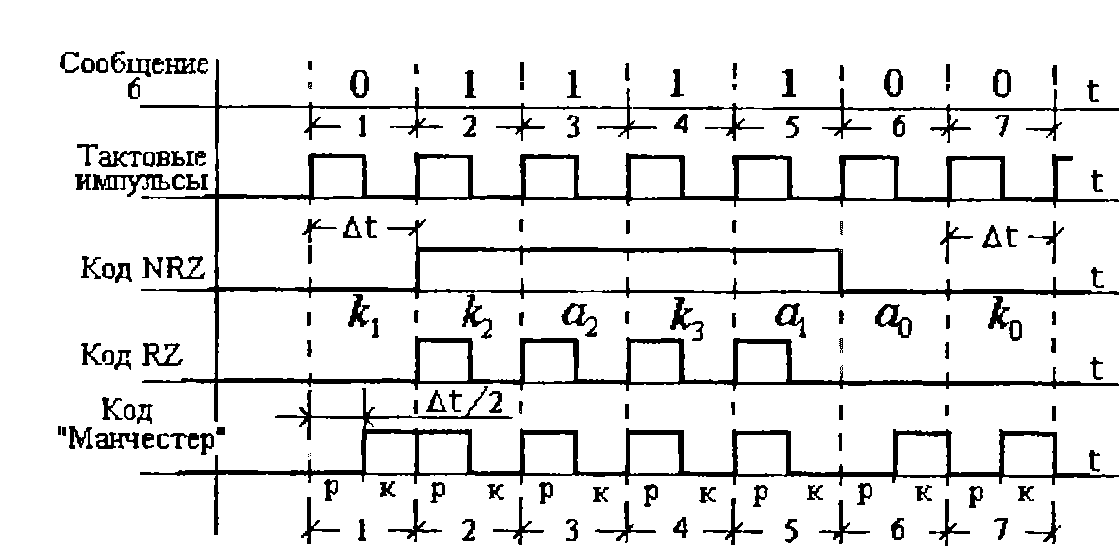
Рис. 3.11. Временные диаграммы сигналов к пояснению кодов NRZ-, RZ- и «Манчестер»
Анализируя диаграмму сигнала кода Манчестер, нетрудно заметить сходство с построением комбинаций корреляционного кода. Действительно, если каждую временную позицию (такт работы системы передачи информации) разделить на две «подпозиции» - рабочую и контрольную, то полученная структура сигнала может быть полностью отображена комбинацией корреляционного кода, рассмотренного выше.
Обратите внимание, на диаграммах рис. 3.11 принято, что сигнал лог.0 отображается отсутствием напряжения либо тока. Если есть возможность, то за сигнал лог.0 следует принять отрицательное напряжение (либо ток), т.е. перейти к использованию полярных признаков. В таком случае можно обеспечить передачу сигналов (и информации) с наибольшей помехоустойчивостью.
Заканчивая рассмотрение корреляционных кодов, следует также отметить, что они применяются для кодирования относительно небольших массивов информации, когда кодовые слова «занимают» не более 2-х...3-х байтов. В противном случае используются циклические либо итеративные коды.

