Как уже было сказано, такие коды имеют минимальное кодовое расстояние, равное единице. Общим свойством всех кодов рассматриваемой группы будет неизбежная трансформация передаваемого сообщения даже при возникновении одиночной ошибки. Ошибки же возникают под действием помех, не отличающихся от параметров передаваемого сигнала. Поскольку помехи носят случайный характер, то ошибки также случайны.
Вторым общим свойством является то, что никаких ограничений на формирование кодовых комбинаций из η элементов с m значениями (признаками) не накладывается Поэтому используются все возможные комбинации, коды являются безызбыточными, равнодоступными и имеют минимальное число элементов. По этой же причине они являются эффективными и непомехоустойчивыми.
Естественно, что такие коды могут использоваться на промежуточных ступенях кодирования (при образовании более сложных кодов) либо для передачи информации по каналам связи без помех.
Двоичные безызбыточные коды. Кодирование
Эти коды имеют основанием число 2 (т = 2). Каждый элемент кода может принимать условные значения 0 и 1. Все элементы являются информационными (n=n0). Согласно выражению (3) мощность кода можно рассчитать по формуле
(4)
Для построения кодирующих устройств двоичными безызбыточными кодами используются следующие процедуры кодирования.
- По заданному количеству кодируемых сообщений (М) рассчитывается по формуле (4) длина (п) кодовых слов так, чтобы N > М.
- Строится таблица кодирования, в которой число столбцов равно длине кодовых слов (n), а число строк - мощности кода (Ν) или числу кодируемых сообщений (М).
- Все сообщения нумеруются десятичными числами, начиная с нуля, а затем по строкам таблицы записываются двоичные комбинации в виде двоичных чисел, являющихся эквивалентом десятичного номера сообщения.
Рассмотрим для примера случай кодирования 8 сообщений (М=8). Согласно изложенной методике, во-первых, определяем длину кодовых комбинаций
Во-вторых, строим таблицу кодирования (см. табл. 1). Для этого все сообщения нумеруем десятичными числами, начиная с нуля, номер сообщения переводим в 3-разрядное двоичное число и записываем его в соответствующую строку таблицы. Таким образом, процедура кодирования сводится к правилам перевода десятичных чисел в двоичные.
Для формализации процедуры кодирования представим двоичное число, отображающее кодовую комбинацию в виде последовательности а2, а1, a0, где логические переменные аj, соответствуют разрядам этого двоичного числа. Причём индекс j есть показатель степени числа 2 (основания системы счисления) при определении весового коэффициента соответствующего разряда числа и одновременно весового коэффициента логической переменной.
Таким образом, переменной а0 и, соответственно, первому элементу кодовой комбинации будет присвоен весовой коэффициент 2° = 1, второму элементу a1 - весовой коэффициент 21=2, третьему элементу а2 - коэффициент 22 = 4.
Таблица 1
Рассматривая табл. 1 как таблицу истинности логических функций а2, а1, а0, и принимая за их аргументы логические переменные х, (ί ε{0, 1, 2,...7}), поставленные в однозначное соответствие кодируемым сообщениям, можно по условиям истинности отыскать следующую систему логических выражений (функций):
(5)
В системе (5) символами «+» обозначена операция дизъюнкции (логического сложения), а каждая функция описывает сигнал на конкретном выходе шифратора. Логическим переменным xi соответствуют входные сигналы шифратора. Используя выражения (5), можно построить принципиальную схему шифратора на релейно-контактных элементах (см. рис. 3.2) либо функциональную схему шифратора на бесконтактных элементах (см. рис. 3.3).
Шифратор (рис. 3.2) состоит из входных цепей (рис. 3.2,а либо рис. 3.2,б) и выходных цепей (рис. 3.2.в). Если выбрать схемы рис. 3.2,а и рис. 3.2.в, то получим неприоритетный шифратор, обладающий существенным недостатком - при попытке одновременного «кодирования» нескольких «сообщений» на выходах может появиться комбинация, не соответствующая ни одному из кодируемых сообщений.
Рис. 3.2. Шифратор двоичного безызбыточного кода на релейно-контактных элементах: схема входных цепей (а и б): схема выходных цепей (в)
Сообщения в рассматриваемой схеме формируются тумблерами SA1-SA7, подающими напряжение питания на входные реле 1P-7Р. Контактами этих реле образованы выходные цепи шифратора. Так, например, если будут включены тумблеры SA2 и SA4, то на выходах шифратора появится комбинация
110, соответствующая сообщению 6. тогда как «кодировались» сообщения 2 и 4 (ем. табл. 1).
Чтобы исключить такое неправильное функционирование шифраторов (с кодированием без приоритета), необходимо исключить возможность одновременной подачи на входы шифратора двух и более входных воздействий. Эго можно сделать, предусмотрев схему, реализующую приоритеты в кодировании входных сигналов (см. рис. 3.2,б). В данной схеме наивысший приоритет присвоен сообщению с меньшим номером. Таким образом, выбрав схемы рис. 3.2,б и рис. 3.2,в, получим шифратор с кодированием по приоритету (приоритетный шифратор). Кроме того, приоритетные шифраторы позволяют использовать комбинацию ООО в качестве «рабочей». Для этого дополнительно организуется выход РИ, на котором сигнал принимает активное значение в тех случаях, когда оказывается включенным хотя бы один из ключей SA0 SA7. В схеме рис. 3.2,б активному значению этого сигнала соответствует уровень лог.0 (отсутствие напряжения). Схему рис. 3.3,а можно получить, представив выражения (5) в виде инверсии логических произведений соответствующих переменных.
Рис. 3.3. Приоритетные шифраторы двоичного безызбыточного 3-элементного кода: схема функциональная шифратора (а); УГО микросхемы К155ИВ1 (б)
Схемы рис. 3.3 приведены в предположении, что основной элементной базой являются микросхемы серий ТТЛ. Напомним, для таких микросхем неподключение входа элемента ни к шине лог.0, ни к шине лог.1 равносильно подаче на этот вход сигнала лог. 1.
Система приоритетов реализуется схемой включения тумблеров SA0, SA1,...SA7. Как видно по схеме, включение тумблера SA7 предотвращает подачу сигналов лог.0 от других тумблеров. Следовательно, схема реализует простую систему приоритетов, когда наивысший приоритет отдан кодируемому сигналу с большим номером. Так же, как и в предыдущей схеме, предусмотрен сигнал РИ, который можно рассматривать как признак кодирования.
Если ни один из указанных тумблеров не включен, то на всех входах логических элементов D1, D2, D3 присутствует сигнал лог.1. Поэтому в исходном состоянии на выходах шифратора сохраняется комбинация 000, соответствующая кодируемому сообщению 0. На выходе РИ присутствует сигнал лог.0, если ни один из тумблеров SA0, SA1,...SA7 не включен, и будет сигнал лог.1 при включении любого из них. Таким образом, для всех входных сигналов активным значением будет уровень лог.0, а для выходных сигналов уровень лог.1.
В интегральном исполнении выпускаются приоритетные шифраторы аналогичного типа, например микросхема К155ИВ1. Её условное графическое обозначение (УГО) приведено на рис. 3.3,б. Это стробируемый приоритетный шифратор 3-элементного двоичного безызбыточного инверсного кода. Согласно УГО, информационные входы (с метками 0, 1, ...7) инверсные, т.е. активным считается уровень лог.0 входных сигналов. Дополнительно есть вход с меткой «Е». Сигналом лог.0 по этому входу даётся разрешение на кодирование входных (информационных) сигналов, а значение лог.1 запрещает кодирование. В состоянии запрета на информационных выходах (с метками 1, 2 и 4) будут постоянно сигналы лог.1 независимо от значений информационных входных сигналов. Наивысший приоритет отдан информационному входу с большим номером (как и в схеме, рис. 3.3,а). Шифратор имеет два дополнительных выхода с метками Р и G соответственно. Сигнал на выходе Р принимает в состоянии «разрешения» значение лог.1, если хотя бы один из сигналов х1 принял значение лог.0 (так же, как и сигнал РИ в схеме рис. 3.3,а). В состоянии разрешения сигнал на выходе G является инверсным сигналу Р. Эти выходы используются для построения шифраторов большей разрядности из микросхем рассматриваемого типа.
Отличие в функционировании шифратора К155ИВ1 от шифратора рис. 3.3,а заключается в том, что сопоставление комбинаций выходных сигналов кодируемым сообщениям выбрано в обратной последовательности (см. табл. 1); сообщению 7 (хт) присвоена комбинация
000; сообщению 6 (х6) - комбинация 001; так далее. Такой код называется инверсным двоичным кодом.
Таблица истинности для микросхемы К155ИВ1 приведена ниже (см. табл. 2).
В ней использованы обозначения входных и выходных сигналов, принятые выше. Если значения входного сигнала безразличны (не влияют на значение выходных сигналов), то в таблице стоит символ «~». Первая выделенная строка таблицы соответствует состоянию, когда наложен запрет на кодирование. А последняя строка табл. 2 отображает случай отсутствия кодирования.
Таблица 2
Двоичные безызбыточные коды. Декодирование
Как было сказано выше, декодирование это процедура обратная кодированию. В общем случае эта процедура сводится к выполнению следующих действий.
- Принятую двоичную комбинацию следует перевести в десятичное число и принять это число за номер декодированного сообщения.
- Сформировать позиционные первичные сигналы, соответствующие декодированным сообщениям.
Чтобы результат декодирования однозначно соответствовал кодированию, необходимо знать последовательность передачи элементов кодовых комбинаций.
Допустим, что передача ведётся в последовательности, определяемой таблицей кодирования (см. табл. 1). Тогда любую принятую комбинацию можно представить в следующем виде: (а2 а1 а0) где индекс i соответствует десятичному номеру принятого сообщения.
Пусть принята комбинация
. Переведём соответствующее этой комбинации двоичное число в десятичное. При этом учитываем весовые коэффициенты переменных, отображающих разряды этого двоичного числа. Тогда получим
.
Таким образом определили, что принято сообщение 6.
Рис. 3.4. УГО микросхемы К155ИД3
Процедуры преобразования двоичных чисел в позиционные сигналы, нумеруемые в соответствии с десятичным эквивалентом декодируемого двоичного числа, реализуются функциональными «узлами» (модулями), называемыми полными декодерами (или дешифраторами). Полный декодер есть комбинационное устройство (функциональный узел), имеющее 2к выходов и к входов, называемых адресными. Выходы дешифратора нумеруются десятичными числами, начиная с пуля. Эти числа - «адрес» выхода - однозначно соответствуют двоичной комбинации (двоичному числу) на адресных входах декодера. Число адресных входов (к) называют «порядком» декодера. Декодер с тремя адресными входами (А=3) будет иметь 23=8 выходов, и такие декодеры являются декодерами третьего порядка. ГОСТ 2.743-81 регламентирует условное графическое обозначение (УГО) полных декодеров. На рис. 3.4 в качестве примера приведено УГО микросхемы К155ИДЗ, являющейся полным стробируемым декодером четвёртого порядка.
Основной алгоритм работы полного декодера состоит в том, что только на одном из множества выходов может появиться сигнал активного уровня. Номер (адрес) активизированного выхода однозначно определяется комбинацией сигналов, присутствующих в рассматриваемый интервал времени на адресных входах декодера. За сигнал активного уровня принимается уровень лог.1, если выходы не инверсные (прямые), и уровень лог.0, если выходы декодера инверсные. Так, у названной микросхемы выходы инверсные и активным уровнем сигнала является лог.О. Кроме адресных входов у рассматриваемого декодера есть входы стробирования (с метками Е1 и Е2). Сигналы по этим входам разрешают либо запрещают декодирование комбинации на адресных входах.
В состоянии запрета декодер становится «нечувствительным» к изменению сигналов по адресным входам и на всех выходах устанавливается уровень лог. 1.
Если входные сигналы обозначить логическими переменными (показаны на рис. 3.4), а выходные сигналы - функциями у то полный декодер четвёртого порядка вида рис. 3.4 можно описать следующей системой логических функций:
Выражение (6) представляет собой обобщённую запись выходных функций декодера. Чертой над переменной и над правой частью выражения обозначена операция инверсии, а символ «~» обозначает наличие или отсутствие символов инверсии адресных переменных. Точкам между переменными соответствует операция логического умножения (конъюнкции). (Допускается точки не ставить). Анализ выражения (6) показывает, что если сигнал, соответствующий переменным s или d, (хотя бы один из них) примет значение лог.1, то на выходах декодера установятся сигналы лог. 1. Это состояние запрета. Чтобы декодер оказался в состоянии разрешения декодирования, необходимо 
. Тогда в зависимости от комбинации вида
на одном из 16 выходов обязательно будет сигнал лог.0. Чтобы определить номер ί активизированного выхода, достаточно перевести комбинацию двоичных сигналов на адресных входах в десятичное число. Например, на адресных входах зафиксирована комбинация 1011. Соответственно
. Переводим двоичное число 1011 в десятичное, получим в результате «11» - число одиннадцать. Перечисленные действия можно оформить следующей записью:
т.е. на выходе с номером i = 11 появится сигнал лог.0.
Из анализа выражения (6) также следует, что полный декодер состоит из набора многовходовых логических элементов типа И-НЕ и дополнительного логического элемента, реализующего функцию ИЛИ-HE над стробирующими сигналами. Так, в рассматриваемой микросхеме содержатся 16 логических элементов типа 5И-НЕ, формирующих выходные сигналы.
В сериях микросхем имеются полные декодеры с прямыми выходами, а также декодеры меньшего порядка. Причём выходы могут быть как инверсными, так и прямыми. Из микросхем полных декодеров меньшего порядка можно строить полные декодеры большего порядка.
Коды Грэя
Разновидностью двоичных безызбыточных кодов являются двоичные рефлексные коды, называемые также кодами Грэя. Эти коды применяются в телеметрических системах, а именно в аналого-цифровых преобразователях, построенных методом «считывания комбинаций». Отличие этих кодов от простого двоичного кода заключается лишь порядком сопоставления кодируемых сообщений кодовым словам. Обычно какая-либо измеряемая физическая величина, например напряжение переменного или постоянного тока, меняется монотонно от меньшего значения к большему, или наоборот. При этом двум последовательным значениям этой физической величины (кодируемым сообщениям) ставят в соответствие комбинации, отличающиеся значением только одного элемента. Таким образом, коды Грэя отличаются от рассмотренного двоичного кода тем, что в комбинациях кода Грэя при «переходе» от одной комбинации к другой меняется только один элемент. В то время как у простого двоичного кода могут меняться одновременно все элементы (разряды), например при кодировании сообщений 3 и 4 (см. табл. 3). В этой таблице приведены комбинации 3-элементного кода Грэя. Между строчками, содержащими соответствующие сообщениям 3 и 4 комбинации, разделительная линия показана удвоенной толщины. Обратите внимание на последовательности комбинаций первых двух элементов (b1, b0) до указанной линии и ниже линии. Эти последовательности как бы зеркально отражены относительно этой линии. Поэтому код получил название рефлексного двоичного кода. Третий элемент комбинаций b2 у первых 4-х комбинаций имеет значение 0, а у последних 4-х - значение 1. Теперь, приняв разделительную линию нижнего края таблицы за плоскость симметрии, можно в зеркальном отображении ниже записать следующие 8 комбинаций. Затем добавить четвёртый элемент b3 кодовых комбинаций и у первых 8 комбинаций придать этому элементу значение 0, а у последних 8-ми - значение 1 и т.д. Таким образом можно построить 4-элементный код Грэя, затем 5-элеменгный и т. д.
Процедуру отыскания комбинаций кодов Грэя можно формализовать как процедуру преобразования комбинаций простого двоичного кода в соответствующий код Грэя.
Для 3-элементного кода Грэя процедура получения комбинаций формализуется следующими логическими выражениями:
(7)
Таблица 3
Таким образом, первый элемент кода Грэя b0 определяется как сумма по модулю два двух первых элементов простого двоичного кода. Второй элемент b1 равен сумме по mod 2 второго и третьего элементов простого двоичного кода и т.д., старшие же разряды кодовых комбинаций одинаковы. По выражениям (7) можно построить функциональную схему кодового преобразователя простого двоичного кода в код Грэя.
Кодирование кодами Грэя позволяет исключить так называемые «ошибки считывания» в соответствующих аналого-цифровых преобразователях. Если на приёмной стороне запоминать предыдущую комбинацию кода Грэя, а затем её сравнивать с принимаемой комбинацией, то можно обнаружить ошибки. Теоретически же коды Грэя но своим свойствам не позволяют обнаруживать ни одной ошибки, т.к. минимальное кодовое расстояние у них равно единице.
Следует заметить, что если для кодирования информации использовано не полное множество комбинаций безызбыточных кодов, то появляется возможность обнаружения ошибок. Можно «обнаружить» те ошибки, которые приводят к неиспользуемым комбинациям. Эти неиспользуемые комбинации считаются запрещёнными. В таком случае говорят, что кодирование выполнено с избыточностью по сообщениям.
Двоично-десятичные коды
В телеметрических системах для представления результатов измерения часто используются двоично-десятичные коды. Обычно количественная оценка результатов измерения осуществляется числами десятичной системы счисления. При этом результат отображается многоразрядным десятичным числом, например 987. Двоично-десятичный код образуется путем замены десятичной цифры разряда двоичным 4-разрядным числом (см. ниже (8)).
Полученная таким образом последовательность символов (единиц и нулей) и будет представлять собой комбинацию двоично-десятичного кода. Для приведённого примера получим последовательность 1001.1000.0111 - это и есть комбинация трёхразрядного двоичнодесятичного кода. Таким образом, мощность двоично-десятичных кодов равна мощности десятичного кода (кода с основанием 10). Как видно по форме записи, последовательность нулей и единиц разбита на тетрады (четыре разряда двоичного числа). Каждая тетрада отображает значение десятичной цифры. Множество значений десятичных цифр {0, 1, 2,...9} ограничивает число двоичных комбинаций, соответствующих тетрадам. В то время как, имея 4 двоичных разряда, можно составить 16 различных комбинаций. Комбинации, соответствующие десятичным числам 10, 11, 12, 13, 14 и 15, являются запрещёнными.
Таким образом, двоично-десятичные коды являются избыточными. Но, в то же самое время, при одной ошибке в тетраде, может произойти трансформация передаваемого сообщения. Например, в тетраде 1001 (она соответствует цифре 9) при передаче произошла ошибка в 4-м элементе, тогда будет принята комбинация 0001. А она соответствует цифре «1» и на приемной стороне будет зафиксирован неверный результат «187», являющийся следствием трансформации переданного сообщения. С другой стороны, одиночные ошибки, приводящие к запрещённым комбинациям, могут быть обнаружены.
Обратите внимание! В рассмотренном примере (см (8)), по умолчанию, было принято, что весовые коэффициенты разрядов тетрад выбраны согласно весовым коэффициентам разрядов двоичных чисел, т.е. «8-4-2-1». Поэтому такие двоично-десятичные коды называют двоично-десятичными кодами с весом «8-4-2-1». Они обладают тем «недостатком», что, в зависимости от десятичной цифры, могут меняться одновременно все разряды тетрады, а число единиц переменно (от 0 до 3). Это затрудняет контроль верности принимаемых комбинаций. Обратитесь к записи (8), первые справа налево две тетрады отображают соответственно цифры 7 и 8. У этих тетрад все разряды имеют противоположные значения!
Чтобы упростить процедуру контроля комбинаций двоично-десятичных кодов, используют «нестандартные» весовые коэффициенты разрядов в тетрадах. Так, применяются двоично-десятичные коды с весом «7-4-2-1», колы с весом «4-2-2-1» и некоторые другие. Первые характеризуются тем, что в «правильных» тетрадах не может быть больше двух единиц, а у вторых (с весом «4-2-2-1») инверсия тетрады есть дополнение до 9 принятой десятичной цифры. Эти признаки кладутся в основу проверок правильности принятых комбинаций (см. табл. 4).
Таблица 4
Двоично-десятичные коды
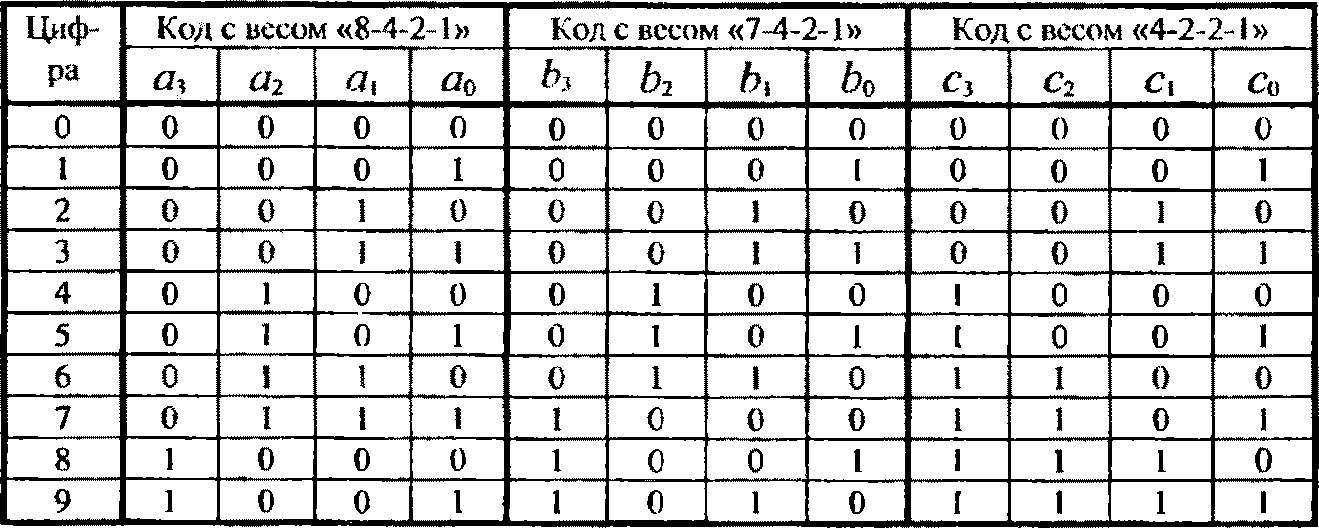
Кодирование двоично-десятичными кодами с весом «8-4-2-1» обычно выполняется стандартными шифраторами, выпускаемыми в интегральном исполнении (например, К555ИВЗ), либо используются кодопреобразователи двоичного кода в названный код, например микросхема К155ПР7.
Для двоично-десятичных кодов с другим весом требуется строить индивидуальные кодовые шифраторы либо индивидуальные кодопреобразователи двоичного кода в рассматриваемый код. Для декодирования рассматриваемых кодов можно применить полные декодеры 4-го порядка выбрав соответствующее подмножество их выходов.
Двоично-десятичные коды используются также в устройствах обработки цифровой информации как промежуточная форма представления чисел и при управлении цифровыми индикаторами, воспроизводящими десятичные цифры.
