3.4. ВОССТАНОВЛЕНИЕ ЭЛЕКТРИЧЕСКОЙ ПРОЧНОСТИ МЕЖДУКОНТАКТНОГО ПРОМЕЖУТКА В ДУ ПРОДОЛЬНОГО ДУТЬЯ
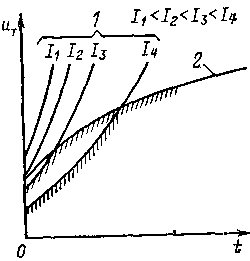
Рис. 3.19. Нарастание электрической прочности промежутка после прохода тока через нуль
Общие сведения.
В результате разрушения дугового столба происходит восстановление электрической прочности дугового промежутка. Существуют два типа пробоя промежутка— тепловой и электрический. При тепловом пробое после прохождения тока через нуль промежуток имеет довольно высокую плотность ионизированных частиц (более 3· 10101/см3), при этом он обладает значительной электрической проводимостью (малым остаточным сопротивлением). Под действием восстанавливающегося напряжения через промежуток протекает остаточный ток, равный Iост=uв/rост. В результате происходит разогрев плазмы, при этом термическая ионизация усиливается. Если теплота, отводимая воздушным потоком, меньше теплоты, выделяемой остаточным током, то термическая ионизация развивается, что в конечном счете ведет к пробою промежутка (положительный энергетический баланс). При отрицательном энергетическом балансе благодаря снижению температуры остаточное сопротивление rост возрастает до бесконечности и процесс отключения завершается. Характерной особенностью теплового пробоя является его относительно медленное развитие во времени (разогрев плазмы).
На рис. 3.19 кривые 1 иллюстрируют ход восстановления электрической прочности при разных токах в случае теплового пробоя. Чем больше ток, тем ниже располагается кривая разрядного напряжения, которое характеризует электрическую прочность.
При электрическом пробое после прохода тока через нуль количество зарядов в промежутке мало (менее 2-1010 см-3), промежуток имеет большое остаточное сопротивление. Восстанавливающееся напряжение стремится пробить этот промежуток. Пробой возникает в результате лавинообразного процесса ионизации в случае, если прочность промежутка ниже восстанавливающегося напряжения.
Электрический пробой может возникать и при небольшой остаточной проводимости. В этом случае вначале возникает тлеющий разряд, который затем переходит в дуговой.
Примерный ход нарастания восстанавливающейся прочности при электрическом пробое показан кривой 2. Тот или иной тип пробоя промежутка определяется начальными параметрами остаточного столба дуги и параметрами воздушного потока.
Процесс восстановления электрической прочности зависит от изменения диаметра дуги. На рис. 3.20 представлены кривые изменения тока в дуге и диаметра столба при подходе к нулю, полученные на макете ДУ. Здесь t — время дο момента прохождения тока через нуль. Направления уменьшения тока и диаметра указаны стрелками. Интересно, что несмотря на крутой спад тока диаметр дуги dд меняется слабо и разрушение столба происходит примерно в течение 4 мкс. Изменение сопротивления дуги при подходе тока к нулю показано на рис. 3.21. Следует отметить, что в интервале времени t>4 мкс сопротивление дуги почти не меняется и мало зависит от давления.
Наиболее круто сопротивление начинает нарастать в течение последних 2 мкс до нуля тока.
Существенное влияние на процесс гашения дуги имеет скорость спада тока при подходе к нулевому значению. Эта скорость зависит от амплитуды тока, шунтирующего конденсатора или резистора и воздействия на дугу охлаждающего потока. Опыт показал, что чем выше перепад давления, тем больше скорость спада тока [3.1].
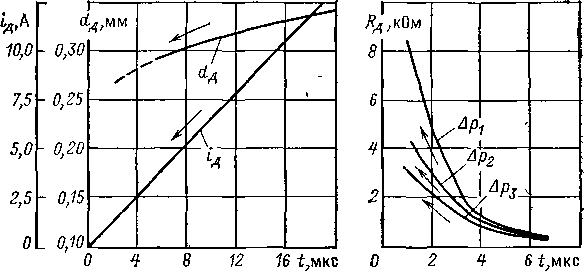
Рис. 3.20. Зависимость диаметра дуги dд от времени вблизи нуля тока:
Δρ=0,35 МПа; dG=l,0 см; 1т =1200 А
Рис. 3 21. Зависимость сопротивления дуги от времени вблизи нуля тока при одностороннем дутье:
Δρ1=0,65 МПа; Δр2=0,32 МПа; Δр3=0,2 МПа; dc = l,0 см
Очень важным параметром дугового столба является его тепловая постоянная времени. По мере перехода тока цепи из дуги в шунтирующий конденсатор подвод энергии к дуге уменьшается и дуговой столб начинает остывать. Чем меньше постоянная времени, тем быстрее охлаждается столб дуги, снижается его температура, восстанавливается электрическая прочность промежутка. В общем случае тепловой баланс единицы длины столба можно выразить уравнением
![]() (3.12)
(3.12)
где h — энтальпия, Дж/кг; S—сечение столба, м2; Е — градиент напряжения на дуге, В/м; σ — удельная электрическая проводимость плазмы, 1/(0м-м); αсж —коэффициент сжатия столба дуги за счет уноса теплоты воздушным потоком (объемное охлаждение),
с-1; k — коэффициент отдачи теплоты через поверхность с единицы длины в единицу времени, отнесенной к единице объема, Вт/м3; γ— плотность плазмы, кг/м3.
В области нуля тока подвод энергии к столбу прекращается, Е=0 и уравнение (3.12) принимает вид
![]()
Решение этого уравнения затруднено тем, что значения h, S, k, σ зависят сложным образом от температуры, места расположения участка в стволе дуги и других факторов.
Задачу можно решить, приняв эти параметры постоянными, для короткого интервала времени. Тогда решение этого уравнения имеет вид
![]()
где ![]()

