3.3. ТЕРМОДИНАМИЧЕСКАЯ ЗАКУПОРКА СОПЛА. РАСЧЕТ ЕГО СЕЧЕНИЯ ПО ЗАДАННОМУ ТОКУ ОТКЛЮЧЕНИЯ
При отсутствии дуги и расхождении контактов в сопле устанавливается критическая скорость истечения воздуха w=√kRT2=330 м/с, так как давление р0 значительно больше критического (см. § 3.6). При наличии дуги происходят быстрый нагрев воздуха в сопле и подъем давления. В результате скорость истечения воздуха падает, причем чем больше ток, тем сильнее торможение воздушного потока. При определенном значении тока происходит термодинамическая закупорка сопла, когда скорость воздуха падает до нуля. Экспериментально наблюдались случаи, когда направление истечения воздуха менялось на обратное — воздух перемещался в направлении к баку. Естественно, при закупорке сопла дуга не гаснет, так как отсутствует необходимый отвод теплоты от нее.
Экспериментально установлено, что для успешного гашения дуги необходимо, чтобы скорость воздуха не опускалась ниже 7—10 м/с при амплитудном значении тока. Задача расчета ДУ заключается прежде всего в том, чтобы выбрать давление в камере р0 и сечение сопла S=πdc/4, при которых скорость истечения не падает ниже 7—10 м/с при амплитуде номинального тока отключения.
Ниже излагается методика, разработанная проф. Г. А. Кукековым [3.1]. При выводах сделаны следующие упрощения: 1) процесс истечения воздуха квазистационарный — параметры воздуха в камере постоянны; 2) тепловая энергия, выделяемая дугой, равномерно распределяется по длине дуги в сопле; 3) течение воздуха происходит без трения.
Принципиальная схема ДУ дана на рис. 3.10, а, схема для расчета — на рис. 3.10, б.
Рассмотрим исходные уравнения для расчетов. Уравнение энергетического баланса
![]() (3.5)
(3.5)
где Q=Рд/Gr — теплота, подводимая к единице массы газа в единицу времени, Вт/кг (Gr—масса газа, кг); ср— теплоемкость газа при постоянном давлении, Дж/(К-кг); Т — температура газа, К; w —скорость газа, м/с.
Первый член правой части — теплота, которая идет на повышение температуры газа, второй — теплота, которая тратится на изменение скорости газового потока.
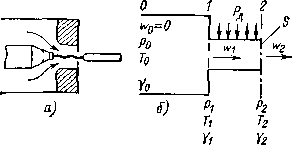
Рис. 3.10. Схема для расчета параметров потока воздуха в ДУ продольного дутья
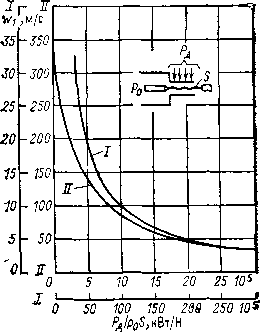
Рис. 3.11. Скорость воздуха на входе в сопло при наличии в нем дуги
Уравнение газового состояния (для единицы массы газа)
![]() (3.6)
(3.6)
где р — давление, Па; ν — удельный объем (объем единицы массы газа), υ=1/γ, м3/кг; γ= Gr/V—плотность газа, кг/м3; R — газовая постоянная, Д—287 Дж/(кг-К).
Составим уравнение расхода газа. В любом сечении, например 1 и 2 сопла, масса газа, протекающего через сопло в 1 с, одинакова:
![]() (3.7) где S — сечение сопла.
(3.7) где S — сечение сопла.
Согласно законам газодинамики соблюдается равенство
![]() (3.8)
(3.8)
Известными являются параметры газа в сечении 0(рис. 3.10). Необходимо найти параметры газа в сечениях 1 и 2. Задача затрудняется тем, что для определения восьми величин (w1, р1, Τ1, γ1, w2, р2, Т2, γ2) имеется всего четыре уравнения.
Для решения задачи можно использовать ряд дополнительных условий. Так, например, давление р2 на выходе воздуха из сопла значительно больше атмосферного, поэтому скорость воздуха w2 достигает критического значения (см. § 3.6):
![]() (3.9)
(3.9)
Привлекая ряд других дополнительных условий [3.1], удается выразить зависимость скорости на входе в сопло от давления в камере, сечения сопла S и мощности дуги Рд=Uд/д. Эта сложная зависимость представлена графически на рис. 3.11. В качестве аргумента используется отношение Рд/p0S. Полный аналитический вывод зависимости W1=f(Рд/p0S) приведен в [3.1].
Эта зависимость позволяет выбрать сечение сопла S, если известны Рд и р0. В современных выключателях р0 меняется от 1 до 5 МПа. Меньшие значения относятся к выключателям низкого напряжения 10—20 кВ, высшие к выключателям высокого и сверхвысокого напряжения (Uном ≥110 кВ).
Мощность дуги Рд=UдIд. В качестве расчетного берется амплитуда номинального тока отключения
![]()
Напряжение на дуге Uд=Εд,срlд. Расчетная длина дуги lд берется условно как расстояние между контактом и наружным срезом сопла. В ДУ с двусторонним дутьем приближенно можно рассматривать два односторонних сопла, включенных последовательно. Мощность, приходящаяся на одно сопло, равна половине мощности, выделяемой в дуге. Расчетная длина дуги равна расстоянию от середины между контактного промежутка до наружного среза сопла. Средний расчетный градиент можно брать равным 150В/см. На рис. 3.11 показаны две кривые—I и II. Первая справедлива при скоростях до 35 м/с, вторая — при скоростях до 330 м/с. Согласно [3.1] зависимости W1=f(p0S/Р0) могут быть представлены упрощенно аналитически. При W1<70 м/с предлагается уравнение

При синусоидальном токе![]() Тогда уравнения для скорости принимают вид:
Тогда уравнения для скорости принимают вид:
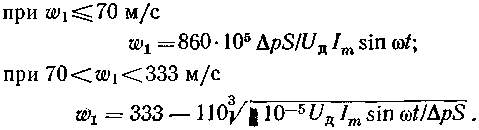
(3.10)
(3.11)
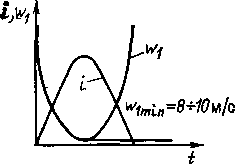
Рис. 3.12. Изменение скорости воздуха в течение полупериода тока
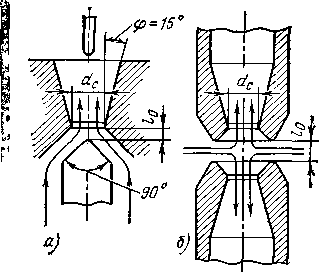
Рис. 3.13. Дугогасительные системы продольного дутья: а — одностороннего; б — двустороннего
Скорость достигает минимального значения при ωt=π/2. По мере уменьшения тока ω1 увеличивается и при ωt=π достигает критического значения 333 м/с. Примерный ход кривой скорости ω1 показан на рис. 3.12. Следует отметить, что по мере уменьшения тока от 1т до 0 за относительно короткий период времени 5 мс w1 должна возрасти примерно с 8 до 333 м/с. При этом на процесс гашения дуги может влиять инерционность воздуха, который необходимо быстро разогнать. В действительности вблизи нуля кривой тока может происходить его резкий обрыв, и, следовательно, можно ожидать больших ускорений воздушного потока. Как показывают расчеты [3.1], время разгона воздушного потока очень мало и составляет единицы микросекунд. Срез тока в области его нулевого значения может быть учтен увеличением его частоты. Если ток меняется по закону то получим
![]()
где kf>l учитывает увеличение крутизны спада тока.
Существенное значение для гашения дуги имеет стабилизация ее в сопле.
При умеренном торможении она удерживается потоком коаксиально внутри сопла, при этом обеспечиваются оптимальные условия тепло- и массообмена и успешное гашение. Такие условия соблюдаются при w1≥wmin=8-10 м/с. При w1<w1min наблюдается нарушение стабилизации дуги, имеет место вращательное движение дуги у входа в сопло. Ионизированные газы занимают большой объем межконтактного промежутка. В результате наступает отказ в гашении даже при оптимальной его геометрии.
Стабилизация столба дуги и термодинамическая закупорка зависят от следующих факторов:
а) геометрической формы дутьевого сопла и формы входной его части, образованной стенками суживающейся части сопла (конфузора) и оконечностью контакта;
б) относительной протяженности между контактного промежутка (длины дуги).
Дугогасительные системы продольного дутья показаны на рис. 3.13. Установлено, что наилучшие результаты в гашении дуги получаются при конической форме сопла (диффузора) и угле φ=15°. Форма входной части выбирается такой, чтобы, с одной стороны, обеспечить оптимальные условия для стабилизации столба дуги воздушным потоком и эффективность разрушения плазмы остаточного столба в конце полупериода. С другой стороны, электрическое поле между контактами, определяемое их формой, должно обеспечивать необходимую электрическую прочность «холодного» промежутка (промежутка, заполненного холодным воздухом после уноса плазмы). Следует отметить, что соблюсти эти два условия трудно. Для получения равномерного воздушного потока необходима острая форма подвижного контакта. При этом отсутствует «мертвая зона», не подвергающаяся воздействию воздушного потока (см. рис. 3.10, а). Однако электрическое поле в этом случае получается резко неоднородным и, следовательно, будет иметь место малая «холодная» прочность промежутка, под которой понимается электрическая прочность при отсутствии дуги. Скругление оконечности контакта (пунктирная линия на рис. 3.10, а) делает электрическое поле более однородным, но ухудшает форму линий воздушного потока. Хорошие результаты получены при несимметричной системе одностороннего продольного дутья [3.7]. В этом случае в подвижном контакте делается отверстие, сообщающееся с атмосферой. Сечение этого отверстия составляет 20—30% сечения сопла. Получено увеличение тока отключения на 25%. Наличие отверстия в контакте способствует устранению «мертвой зоны» в области конца контакта. Такое ДУ использовано в модернизированном выключателе серии ВВБК(§3.9).
Существенное значение для процесса гашения дуги имеет расстояние между контактами. С увеличением длины дуги увеличивается энергия, выделяемая ею, и, следовательно, возрастает торможение воздушного потока. В результате к концу полупериода к месту разрыва остаточного столба поступает не холодный воздух, а горячий, медленно нарастает электрическая прочность промежутка и дуга не гасится.
При малом расстоянии между контактами ограничивается доступ воздуха в сопло.
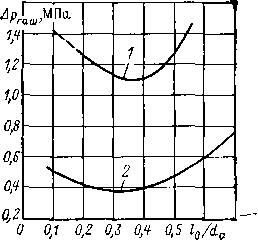
Рис. 3.15. Зависимость перепада Δρ, необходимого для гашения за один полупериод, от относительного расстояния между контактами:
1 —dc=0,56 см; 2 — dc=l,0 см
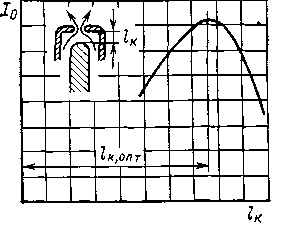
Рис. 3.14. Зависимость мощности (тока) отключения от расстояния между контактами.
В результате не обеспечивается необходимое воздействие воздушного потока на столб дуги. Существует оптимальное расстояние между контактами, при котором происходит наиболее эффективное воздействие потока на столб дуги. Для ДУ с двусторонним дутьем с точки зрения расхода воздуха оптимальное рас-* стояние lд определяется условием
![]()
где πdclд — поверхность цилиндра, через которую воздух поступает; 2πdc/4— сечение двух сопл, через которые воздух уходит.
Полученное соотношение lд=0,5 dc довольно близко к экспериментальному. На рис. 3.14 представлена экспериментальная зависимость тока отключения от расстояния между контактами 1к для ДУ одностороннего дутья. Аналогичная кривая получена для ДУ двустороннего дутья.
В процессе отключения дуга, перемещаясь потоком воздуха, может иметь длину во много раз большую, чем оптимальное расстояние между контактами Ζκ, опт. Для уменьшения длины дуги в ДУ устанавливаются специальные ограничивающие электроды, между которыми дуга горит после того, как основания ее начнут перемещаться по внутренней поверхности сопла (см. рис. 3.47, поз. 41).
Интересны результаты, полученные в [3.1] и показанные на рис. 3.15. По вертикальной оси отложен перепад давления, обеспечивающий гашение дуги за один полупериод, по горизонтали —отношение l0/dc. При данном диаметре сопла dc существует оптимальное расстояние, при котором гашение дуги происходит при наименьшем перепаде ∆р (см. рис. 3.13). Расстояние для одностороннего дутья составляет (0,3-0,4)dc. Интересно отметить, что при уменьшении диаметра сопла dc с 1 до 0,56 см возрастает с 0,38 до 1,1 МПа. При этом сохраняется равенство ∆pS—const.
Опытным путем установлено, что расстояние соответствует пути перемещения холодных частиц воздуха от конца контакта до переднего среза горловины сопла за время, равное полупериоду тока. Для расчета lо.опт необходимо знать скорость воздушного потока, которая является функцией времени и положения точки в сопле.
Представляет интерес сравнение сопл одно- и двустороннего дутья. В сопле одностороннего дутья удается получить лучшее поле воздушного потока, отсутствие «мертвых зон». Недостатком этого сопла является испарение металла электродов в зону дугового столба, что ухудшает процесс гашения дуги, так как потенциал ионизации паров металлов значительно ниже, чем газа (в основном азота). При двустороннем дутье пары металла выносятся из зоны между контактного промежутка, что способствует процессу гашения дуги. Однако в этом сопле воздушный поток подходит вначале перпендикулярно дуге, а затем разворачивается на 90°. В результате в месте поворота потока возникает «мертвая зона», в которой ослаблено воздействие воздуха на столб. В этом месте столб дуги имеет увеличенный диаметр. На рис. 3.16 представлена экспериментальная зависимость Δρ от относительного расстояния, при котором дуга гаснет за один полупериод [3.1].
Из кривых 1 и2 следует, что одностороннее дутье требует большего давления (примерно в 1,6 раза), но зато расход воздуха снижается в 2 раза по сравнению с двусторонним дутьем.
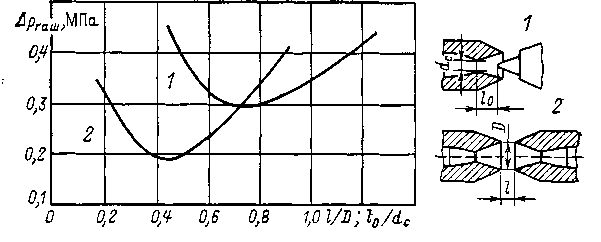
Рис. 3.16. Сравнение сопл одностороннего (1) и двустороннего (2) дутья
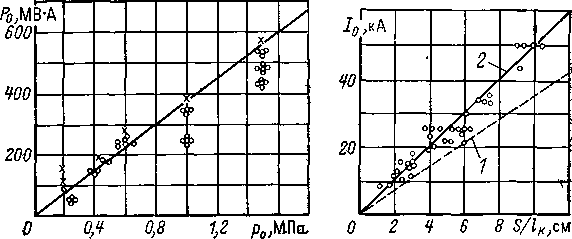
Рис. 3.18. Зависимость тока отключения от отношения сечения сопла S, см2, к расстоянию между контактами lк, см
О — отключено; х — не отключено
Рис. 3.17. Зависимость мощности отключения от давления:
Скорость истечения w1=w1кр=333 м/с одинакова для обоих случаев, но при двустороннем дутье имеется два сопла. Можно принять, что при одностороннем дутье ток отключения составляет примерно 0,8 тока отключения для двустороннего дутья.
В заключение следует отметить, что для одностороннего дутья можно принимать минимальное значение 0,33, для двустороннего —0,5.
Рассмотрим зависимость тока (или мощности) отключения от давления р0 и диаметра сопла ДУ. Для выбранного значения w1 фактор![]() S является постоянной.
S является постоянной.
При увеличении давления ток 1т также должен возрасти. Таким образом, ток отключения и мощность отключения пропорциональны давлению (рис. 3.17). Электрическая прочность промежутка также растет с увеличением давления, что позволяет увеличивать номинальное напряжение выключателя или допустимую скорость восстановления напряжения. Следует отметить, что увеличение давления требует упрочнения элементов выключателя и усложнения условий работы клапанов системы управления воздушного выключателя. Все это вызывает утяжеление выключателя. В настоящее время для самых мощных выключателей р0≤5 МПа.
Ток отключения также пропорционален сечению сопла S. Экспериментальная зависимость приведена на рис. 3.18. Учитывая, что в процессе испытания имеется разброс результатов, на рис. 3.18 обозначены: 1 — нижний предел, 2— средняя кривая тока отключения. Возрастание 5 ведет к увеличению расхода воздуха и объема бака выключателя.

