Волноводные линии передачи - Типы волн в волноводе прямоугольного сечения

2 Волноводы прямоугольные, круглые, П- и Н-образного сечения
ТИПЫ ВОЛН В ВОЛНОВОДЕ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ

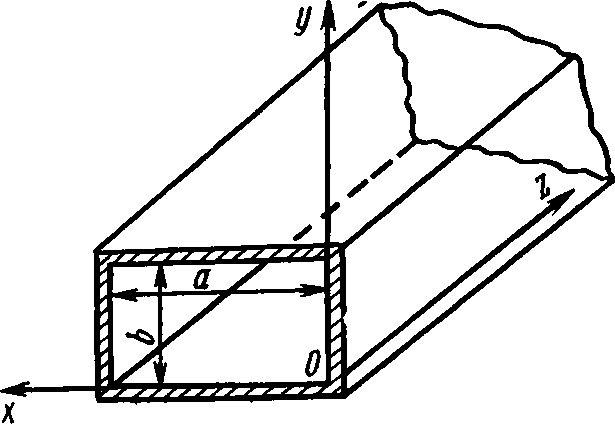
Рассмотрим волновод, представляющий собой металлическую трубу прямоугольного сечения. Обозначим через а широкую стенку прямоугольника, а через b его узкую стенку. Оси прямоугольной системы координат расположим так, как показано на рис. 2.1. При этом примем, что волновод имеет бесконечную длину, идеальную проводимость и однородное по длине сечение стенок.

Рис. 2.1. Волновод прямоугольного сечения и расположение осей координат

В волноводе прямоугольного сечения могут быть возбуждены как электрические волны типа Е, так и магнитные типа Н. При анализе электрических волн типа Е, характеризующихся тем, что составляющая напряженности магнитного поля Ηz=0, следует воспользоваться волновым уравнением (1.84). Решая это уравнение методом разделения переменных, получим следующие выражения для составляющих напряженности электрического и магнитного полей:

В этих выражениях E0 — амплитуда напряженности электрического поля, определяемая мощностью источника; т и п — любые целые числа; Z — волновое сопротивление, определяемое по формуле (1.95); γ — коэффициент распространения волны; f — частота; fкр — критическая частота. Множитель  определяет характер изменения составляющих векторов Е и Н вдоль оси z.
Для магнитных волн типа Н, характеризующихся тем, что составляющая напряженности электрического поля Ez=0, решая аналогичным образом волновое уравнение (1.85), можно получить:

При решении волновых уравнений (1.84) для волн типа Е и (1.85) для волн типа Н получается, что

Рис. 2.2. Структура электромагнитного поля некоторых видов электрических волн в волноводе прямоугольного сечения

Критическая длина волны в соответствии с (1.102) будет

(2.13)
Формулы (2.12) и (2.13) показывают, что максимальное значение критической длины волны и минимальная критическая частота будут при наименьших значениях т и п.
Для магнитной волны Н минимальные значения т и п могут быть: т=1, п=0 или т=0, п=1.

Рис. 2.3. Структура электромагнитного поля некоторых видов магнитных волн в волноводе прямоугольного сечения
В первом случае λкр=2а (волна Н01), а во втором случае λκρ=2b (волна Н01).
Учитывая, что  

Продольная составляющая магнитного поля для волны определится из уравнения

Для применяемых волноводов прямоугольного сечения величина волнового сопротивления получается равной примерно 300— 500 Ом. Например, для волновода сечением 11X5,5 мм² при длине волны 1,5 см волновые сопротивления по напряжению и току, мощности и току, напряжению и мощности получаются соответственно равными 405, 318 и 515 Ом, а для волновода сечением 48x24 мм² при длине волны 6 см — соответственно 379, 298 и 482 Ом.
Структура электромагнитного поля волны показана на рис. 2.3. Как видно из рисунка, в плоскостях, параллельных широким стенкам волновода, расположены замкнутые магнитные силовые линии. Следовательно, согласно уравнениям Максвелла эти линии должны охватывать токи проводимости или токи смещения. В рассматриваемом случае магнитные силовые линии охватывают токи смещения, текущие между широкими стенками параллельно оси у. Максимальная плотность тока смещения будет в центре замкнутых магнитных силовых линий, где напряженность электрического поля равна нулю.
Рассмотрим кратко вопрос о распределении плотностей токоd проводимости на стенках волновода прямоугольного сечения.  

Предположим, что стенки волновода обладают идеальной проводимостью и, следовательно, токи текут по поверхности стенок. Плотность этих токов численно равна напряженности магнитного поля у поверхности проводника. Вектор плотности поверхностного тока будет перпендикулярен направлению вектора напряженности магнитного поля. Поэтому, зная напряженности магнитного поля, нетрудно определить плотности токов. У поверхности широких стенок (см. рис. 2.3) имеются две составляющие вектора напряженности магнитного поля: Нх и Ηz. В соответствии с этим на стенках будут составляющая плотности тока σz, параллельная оси z и называемая продольным током, и составляющая плотности тока σx, параллельная оси х и называемая поперечным током. Используя уравнение (2.15), получаем следующее выражение для амплитуды плотности продольного тока на широкой стенке:

Рис. 2.4. Распределение плотностей: а) продольного и б) поперечного токов в волноводе прямоугольного сечения

Графически зависимость амплитуды плотности продольного тока показана на рис. 2.4a. Амплитуда плотности поперечного поверхностного тока на широких стенках волновода может быть определена из формулы (2.17):
(2.27)
Распределение плотности поперечного тока показано на рис. 2.4б. Из этого рисунка видно, что плотность поперечного поверхностного тока вдоль средней линии широкой стенки волновода равна нулю.
На узких стенках волновода поверхностный ток определяется только составляющей Ηz магнитного поля и имеет только составляющую σу. Из уравнения (2.17) следует, что у узких стенок Ηz имеет постоянную амплитуду, равную H0. Поэтому плотность поверхностного тока на узких стенках будет равна
(2.28)

В любой точке поверхности широких стенок волновода суммарная плотность тока будет равна
(2.29)

Рис. 2.5. Распределение токов в стенках волновода

Распределение суммарной плотности тока по стенкам волновода показано на рис. 2.5. Из этого рисунка видно, что для основной волны в прямоугольном волноводе имеет место большая плотность поперечных токов, идущих через ребро волновода. Это требует хорошей проводимости реберных швов. В то же время для волн типа Е поперечные токи отсутствуют и реберные швы могут даже не иметь электрического контакта. Поэтому распределение токов по стенкам волновода важно знать при его конструировании.