Для передачи электромагнитной энергии высокой частоты используются в ряде случаев волноводы П- и Н-образного сечения. Эти волноводы представляют собой видоизмененную конструкцию прямоугольного волновода. Волновод П-образного сечения показан на рис. 2.28, а волновод Н-образного сечения — на рис. 2.29. По сравнению с прямоугольными волноводами П- и Н-волноводы имеют более длинную критическую волну и более низкое характеристическое сопротивление при одинаковых внешних размерах. При одинаковых критических волнах можно получить П- и Н-волноводы меньших габаритов по сравнению с прямоугольными волноводами. Кроме того, П- и Н-волноводы обладают более широкой полосой пропускания, свободной от высших типов колебаний.
Благодаря указанным преимуществам П- и Н-волноводы можно использовать как: линии передачи в системах, предназначенных для работы на основном типе колебаний в широком диапазоне частот; согласующие или переходные элементы в волноводно-коаксиальных соединениях; элементы фильтров и для других целей. Волноводы типов П и Н могут применяться также в качестве выходных трансформаторов в магнетронах для преобразования высокого характеристического сопротивления волновода, используемого для передачи колебаний, в малое сопротивление магнетрона. Если для этой цели применять прямоугольный волновод, то размеры согласующего устройства окажутся слишком большими.
Волноводы типов П и Н работают одинаково; выбор типа определяется условиями применения и механическими соображениями. Волновод типа Н более предпочтителен для длинных линий передачи, так как высота каждого выступа приблизительно вдвое меньше, чем в волноводе типа П.


Рис. 2.29. Сечение Н-образного волновода
Это облегчает соблюдение допусков на выступ и упрощает производство гибкого волновода. Волновод типа П наиболее пригоден для переходов к коаксиальной линии.
Однако П- и Н-волноводы имеют и некоторые недостатки. Затухание в этих волноводах получается несколько выше по сравнению с прямоугольными волноводами. Наличие прямоугольных выступов внутри волновода вызывает большую концентрацию электрического поля, что понижает допускаемый предел передаваемой мощности. Закругление выступающих углов, применяемое на практике, в значительной мере устраняет этот недостаток.
Параметры П- и Н-волноводов к настоящему времени теоретически изучены сравнительно полно. Большинство иностранных авторов за основу теоретического расчета параметров П- и Н-волноводов принимают метод эквивалентных схем на основе теории длинных линий. Этот метод является весьма приближенным и дает в ряде случаев значительные расхождения с экспериментальными данными. Советскими учеными [7—11] предложены методы расчета параметров П- и Н-волноводов на основе решений основных уравнений электромагнитного поля. Параметры волноводов, рассчитанные по этим методам, хорошо совпадают с экспериментальными данными.
Основной волной в П- и Н-волноводах, так же как в волноводах прямоугольного сечения, является магнитная волна типа Н10. Этот тип волны в основном и рассматривается при расчете параметров П- и Н-волноводов.
Как видно из рис. 2.29, волновод Н-образного сечения можно рассматривать как волновод, состоящий из двух одинаковых П-волноводов. Поэтому выводы, полученные, например, для П-волноводов, будут справедливы также и для Н- волноводов, так как ввиду зеркальной симметрии поля волны Н10 в Н-волноводе относительно горизонтальной оси и выполнения на этой оси граничного условия Н-волновод можно разделить на два одинаковых П-волновода, не изменяя критической длины волны. Следовательно, Н-волновод имеет такую же критическую частоту, как и соответствующий П-волновод, но за счет отсутствия разделяющего проводника обладает вдвое большим характеристическим сопротивлением и несколько меньшим коэффициентом затухания.
Для нахождения критической длины волны П- и Н-волноводов необходимо решить следующее двумерное дифференциальное уравнение, описывающее поле в плоскости поперечного сечения волновода:
![]()
(2.112)

Рис. 2.30. К расчету критической частоты П-волновода
При этом для волн типа Н0т граничным условием является дН/дп = 0.
Решая уравнение (2.112) и находя собственные числа волнового уравнения k, находим критическую длину волны, которая будет равна
![]() (2.113)
(2.113)
Решение уравнения (2.112) для поперечных сечений сложной формы, подобных П или Н, весьма затруднительно, а точного решения с помощью конечного числа известных функций получить вообще невозможно. Некоторые авторы определяют критическую длину волны в П- и Н-волноводах, представляя волновод эквивалентной схемой и рассматривая в этой схеме условия резонанса. Точность этого сравнительно простого метода зависит от геометрических соотношений в П- и Н-волноводах и во многих случаях оказывается недостаточной. Метод, предложенный Л. Н. Дерюгиным, дает результаты, на точность которых геометрические соотношения не влияют. Рассмотрим более подробно сущность этого метода.
Для волн Н10 можно ограничиться рассмотрением лишь Г-образной области рис. 2.30, так как функция Н (х, у) является нечетной относительно переменной х. При этом вводится дополнительное граничное условие на оси у, согласно которому при х = 0 напряженность магнитного поля Нх = 0.
Решение волнового уравнения (2.112) для сложной Г-образной области отсутствует. Поэтому эта область разбивается на две простые области — I и II (см.
рис. 2.30), для которых решения известны. При согласовании этих решений получается интегральное уравнение, в котором единственным неизвестным является собственное число k.




Решая это уравнение методом Галеркина, можно получить выражение для критической волны в П-волноводе λ'кр в зависимости от геометрических размеров. Получаемые выражения сложны для практических расчетов, поэтому Л. Н. Дерюгин составил графики, значительно упрощающие определение критической длины волны. Эти графики, приведенные на рис. 2.31— 2.34, выражают зависимость коэффициента понижения η, представляющего собой отношение критической длины волны соответствующего прямоугольного волновода к критической длине волны П-волновода (η=λκρ/λ'κρ), от геометрических размеров П- и Н-волноводов.
Величина η всегда меньше единицы, так как критическая длина волны П- и Н-волноводов λ'κρ всегда больше критической длины прямоугольного волновода λкр с размерами 2l и h. Каждый из графиков относится к фиксированному значению отношения b/l, равного 1,0; 0,75; 0,5 и 0,25. Если при принятых размерах волноводов значения а/l и h/l отличаются от фиксированных значений графиков, то величину η надо определять по правилам интерполяции. Для промежуточных значений h/l можно применять линейную интерполяцию, а для промежуточных значений а/l целесообразнее пользоваться параболической интерполяцией.
Используя графики рис. 2.31 и 2.32, можно по заданной критической частоте и трем размерам определить четвертый недостающий размер волновода.
При дальнейших исследованиях было предложено решать уравнения согласования методом неопределенных коэффициентов. В этом случае для волны типа H10 формула для определения собственного числа в первом приближении получается следующей:

При использовании этих формул были рассчитаны [11] критические частоты некоторых типов Н-волноводов. Результаты расчетов приведены в табл. 2.10.
Таблица 2.10
Критические длины волн, мм, для некоторых типов Н-волноводов

.Анализ данных табл. 2.10 показывает, что критическая длина волны для Н- волноводов значительно больше, чем для волноводов прямоугольного сечения аналогичных размеров. Так, например, для волновода № 3 критическая длина волны при выполнении его прямоугольным будет равна λкр Н10 = 2-34 = 68 мм, а для Н-волновода λ'κρ = 131 мм.
Критическая длина волны может быть приближенно рассчитана при замене П- и Н-волноводов эквивалентной схемой резонансного контура из сосредоточенных индуктивности и емкости. В этом случае формула для определения критической длины волны при колебаниях типа Н10 имеет следующий вид:

Компоненты электромагнитного поля, необходимые для использования формулы (2.118), могут быть определены, исходя из выражений для областей I и II (см. рис. 2.31), получаемых при решении уравнения (1.103). Тогда после интегрирования соответствующих выражений можно получить следующую формулу для определения коэффициента затухания волны Н10 в Н-волноводе:

При использовании этой формулы необходимо знать собственное число k, которое может быть определено из (2.114).

Рис. 2.35. Зависимость коэффициента затухания Н-волновода от частоты (кривая 1 — волновод № 4, табл. 2.10; кривая 2 — волновод № 5) и прямоугольного волновода (кривая 3)
Рис. 2.36. Зависимость коэффициента затухания Н-волновода от частоты (волновод № 6, табл. 2.10)
На рис. 2.35 и 2.36 приведены для примера результаты расчета коэффициента затухания 4, 5 и 6-го медных Н-волноводов табл. 2.10. Сравнение кривых 1 и 2 рис. 2.35 показывает, что затухание Н-волноводов при одних и тех же габаритных размерах будет тем больше, чем меньше величина g, т. е. чем больше выступ волновода. Однако увеличение затухания компенсируется расширением полосы частот, пропускаемой волноводом. На этом же рисунке (кривая 3) приведено значение коэффициента затухания прямоугольного волновода таких же габаритов (23X10 мм2). Отсюда видно, что, как и следовало ожидать, значение этого коэффициента несколько меньше, чем у соответствующего Н-волновода. Данные рис. 2.35 показывают, что с уменьшением габаритов Н-волновода его коэффициент затухания значительно возрастает.
Формула (2.119) может быть использована также для расчета коэффициента затухания П-волновода. В этом случае при подстановке в (2.119) значения

Значения Ζв∞ для волноводов, приведенных в табл. 2.10, даны в табл. 2.11.
Таблица 2.11
Волновое сопротивление на бесконечно большой частоте и предельные мощности для некоторых типов Н-волноводов
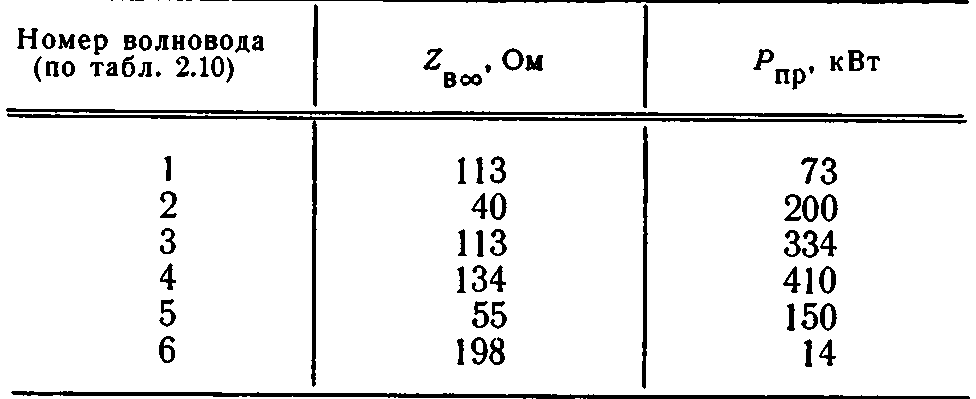
Зная значения Ζв∞, легко определить по формуле (2.123) величину характеристического сопротивления Ζв на любой частоте диапазона.

На рис. 2.37 (кривая 1) приведена частотная зависимость волнового сопротивления Н-волновода (№ 4, табл. 2.10). На этом же рисунке приведено волновое сопротивление прямоугольного волновода (кривая 2) таких же габаритных размеров. Сравнение кривых показывает, что Н-волновод позволяет получить значительно меньшее волновое сопротивление по сравнению с прямоугольным волноводом.
Для приближенного определения волнового сопротивления может быть применен более простой метод эквивалентной схемы. В этом случае волновое сопротивление П-волновода на бесконечно большой частоте определяется по формулам (2.121) и (2.122). Волновое сопротивление на любой частоте диапазона может быть найдено по формуле (2.123). В случае Н-волновода значение Ζв, определенное для П-волновода, должно быть удвоено.
Предельная мощность Н-волновода, так же как и прямоугольных волноводов, определяется исходя из предельной напряженности электрического поля Епр. Для воздуха при нормальном давлении и температуре Епр принимается равным 3,0 кВ/мм. Зная напряженности поля в волноводе, можно найти поток мощности в волноводе и максимальное значение электрического поля в его поперечном сечении для рассматриваемого типа волны. Приравнивая найденное максимальное значение электрического поля к величине Епр, можно выразить поток мощности через Епр, т. е. определить предельную мощность волновода.
Можно показать, что предельная мощность Н-волновода на бесконечно большой частоте для волны Н10 определяется по формуле
![]()
(2.125)
Предельная мощность на любой частоте диапазона волновода может быть рассчитана по формуле
![]()
Рассчитанные значения Рпр∞ для некоторых типов Н-волноводов приведены в табл. 2.11.

