Предлагается следующая модель накопления объемного заряда, основанная на теории электронных лавин Таунсенда с учетом процессов прилипания электронов к молекулам [6, 9].
Необходимые для количественных оценок значения а/p и η/ρ, т. е. отношений коэффициента ударной ионизации газа а к его давлению р и коэффициента прилипания электронов η к р использовались как табличные функции по данным Гаррисона и Джеболла [13, 14]. При конструировании модели процесса были приняты следующие упрощающие допущения.
- Время формирования электронной лавины в сильном электрическом поле около поверхности электрода с меньшим радиусом кривизны много меньше периода колебаний высокочастотного напряжения, приложенного к разрядному промежутку. Поэтому принималось, что лавина образуется мгновенно и ее характеристики соответствуют тому значению электрического поля, которое было в рассматриваемый момент времени.
- Искажение электрического поля пространственным зарядом не учитывалось. Такое допущение может быть справедливым до напряжений, меньших разрядного напряжения на несколько процентов.
- Напряженность электрического поля Е(х) вдоль центральной силовой линии в точках на расстоянии х от электрода с меньшим радиусом кривизны рассчитывалась по формуле для радиального поля (см. [15])
(1-2)
где kн — коэффициент неоднородности электрического поля для данного разрядного промежутка (например, шар—плоскость), r0— радиус кривизны электрода с меньшим радиусом кривизны (шара), п — показатель степени, определяющий быстроту изменения электрического поля с изменением х, и — напряжение между электродами (мгновенное значение), L — расстояние между электродами вдоль центральной осевой линии.
Опускаем подробный ход рассуждений, приводим только поясняющие моменты.
Число электронов в лавине пе, образованных электроном, стартующим вдоль центральной силовой линии от электрода с меньшим радиусом кривизны, и прошедшим расстояние х,
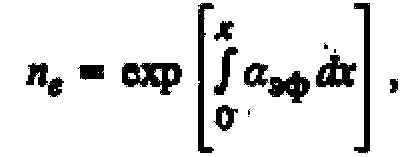
(1-3)
где
— эффективный коэффициент ударной ионизации.
Количество положительных п+ и отрицательных п_ ионов, образованных этой же лавиной
(1-4)
Для учета поглощения положительных ионов электродом с меньшим радиусом кривизны г0 рассмотрим рис. 1-7, а—д. Пусть электрон образовал лавину в момент амплитудного значения отрицательного напряжения на вершине шара (см. рис. 1-7,а). В течение следующей четверги полупериода положительный объемный заряд хвоста лавины длиной l+ (амплитуда колебания иона) поглотится на шаре (рис. 1-7,б). В дальнейшем остаток объемного положительного заряда удалится к противоположному электроду (к плоскости) (рис. 1-7,в,г) и будет колебаться между электродами, размываясь благодаря процессам расталкивания, диффузии и турбулентного движения воздуха. Определенная часть ионов, пропорциональная общему объемному заряду, будет захвачена потоком воздуха и отмечена как ток положительных ионов на коллектор (1+). Аналогичные рассуждения можно привести и для отрицательного объемного заряда (см. рис. 1-8, а—d).
Рис. 1-7. Фазы изменения объемного положительного заряда в разрядном промежутке шар—плоскость за один период ВЧ напряжения
Рис. 1-8. Фазы изменения объемного отрицательного заряда в разрядном промежутке шар—плоскость за один период ВЧ напряжения
Вычисления показывают, что при амплитудном значении напряжения
(1-5)
Так как подвижности положительного
и отрицательного
ионов в воздухе мало отличаются, то принималось, что l+=l_.
Приведенные рассуждения позволяют найти формулу для числа положительных ионов, накапливающихся в разрядном промежутке за полупериод при непрерывной эмиссии фотоэлектронов с поверхности шара, и умножив это число на частоту, определить количество зарядов, образующихся и накапливающихся в единицу времени.
Учитываются также следующие процессы ухода (убывания) отрицательного и положительного объемного заряда из разрядного промежутка:
диффузия к электродам;
рекомбинация положительного и отрицательного зарядов;
ускользание ионов вместе с потоком воздуха;
турбулентное перемешивание, ведущее к повышенным значениям ускользания на электроды.
Через много периодов внутри разрядного промежутка устанавливается равновесное количество отрицательного и положительного объемного заряда, не зависящее от времени. Это произойдет, когда количество ионов, образованных внутри разрядного промежутка в единицу времени станет равным количеству ионов, убывающих из разрядного промежутка вследствие одновременного действия всех перечисленных факторов в эту же единицу времени.
Вычисления позволяют определить отдельно р+ и р_ — средние объемные плотности положительного и отрицательного объемного заряда:
где b — показывает, какая часть заряда попадает на коллектор.
Эти токи измеряются экспериментально на установке, описанной ранее, и результаты расчета можно сравнить с экспериментом.
1-5. Измерения характеристик положительного и отрицательного объемных зарядов
Были измерены зависимости тока положительных I+ (Um) и отрицательных 1_ (Um) ионов на коллектор от амплитудного значения напряжений высокой частоты для разрядных промежутков различной формы. Для примера на рис. 1-9 показаны зависимости I+ (Um) для промежутка плоскость—плоскость с расстоянием между электродами от 0,8 до 1,8 мм при частоте 3 МГц. По оси ординат отложено значение тока на коллектор в полулогарифмическом масштабе. Ток возрастает с ростом напряжения почти экспоненциально и увеличивается от момента своего обнаружения на три порядка, т.е. в тысячу раз, пока напряжение не станет близким к пробивному.
Рас. 1-9. Зависимость тока положительных ионов на коллектор от напряжения частотой 3 МГц
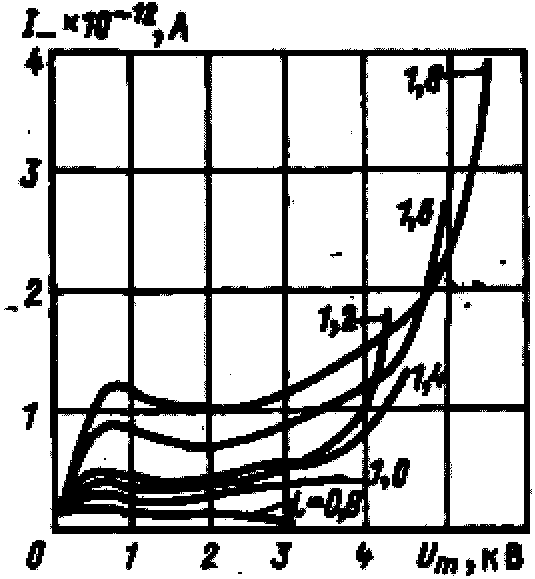
Рис. 1-10. Зависимость тока отрицательных ионов на коллектор от напряжения частотой 7 МГц
На рис. 1-10 представлены типичные зависимости тока отрицательных ионов от амплитудного напряжения. Функция I_ (Um) более сложная, чем для положительных ионов. В зависимости от расстояния между электродами имеется один или два максимума. Второй максимум обнаруживается для более длинных промежутков при меньших частотах. Ток I_ отложен по оси ординат в линейном масштабе.
На рис. 1-11 представлены экспериментальные зависимости тока I+(Um) для разрядного промежутка шар—плоскость при различных частотах.
На рис. 1-12 и 1-13 представлены данные измерений зависимостей I-(Um) и I+(Um) для промежутка острие—плоскость. Наблюдается четкая экспоненциальная зависимость I+ от напряжения. Чем выше частота, тем раньше можно обнаружить положительный объемный заряд. Ток отрицательных ионов I_ начинается практически от нуля напряжения и быстро растет, достигая значения 10-13 А, после чего рост I_ замедляется. Перед пробоем ток I_ опять резко возрастает.
На рис. 1-14 и 1-15 приведены результаты сравнения теории и эксперимента для разрядного промежутка шар—плоскость. Штриховые кривые вычислены с помощью ЭВМ по формулам (1-6—1-10). Сплошные кривые — экспериментальные.
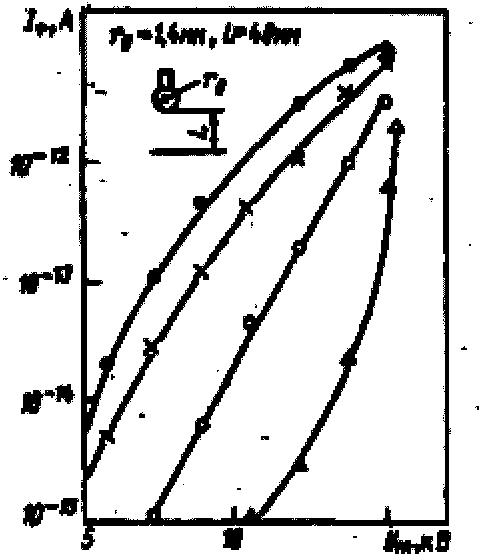
Рис. 1-11. Зависимость тока положительных ионов на коллектор от напряжения ВЧ для разрядного промежутка шар—плоскость при различных частотах:
• - 1000 кГц; х - 200; о — 100; ∆ - 50
Рис. 1-13. Зависимость тока отрицательных ионов на коллектор от напряжения ВЧ для разрядного промежутка острие—плоскость. Обозначения те же, что и на рис. 1-12
Экспериментальные и теоретические зависимости I+ (Um) для данного разрядного промежутка удовлетворительно совпадают при исследованных частотах. Правильно описывается общий ход поведения кривых I_(Um): при малых напряжениях U_ медленно растет с увеличением напряжения, при больших напряжениях — быстро.
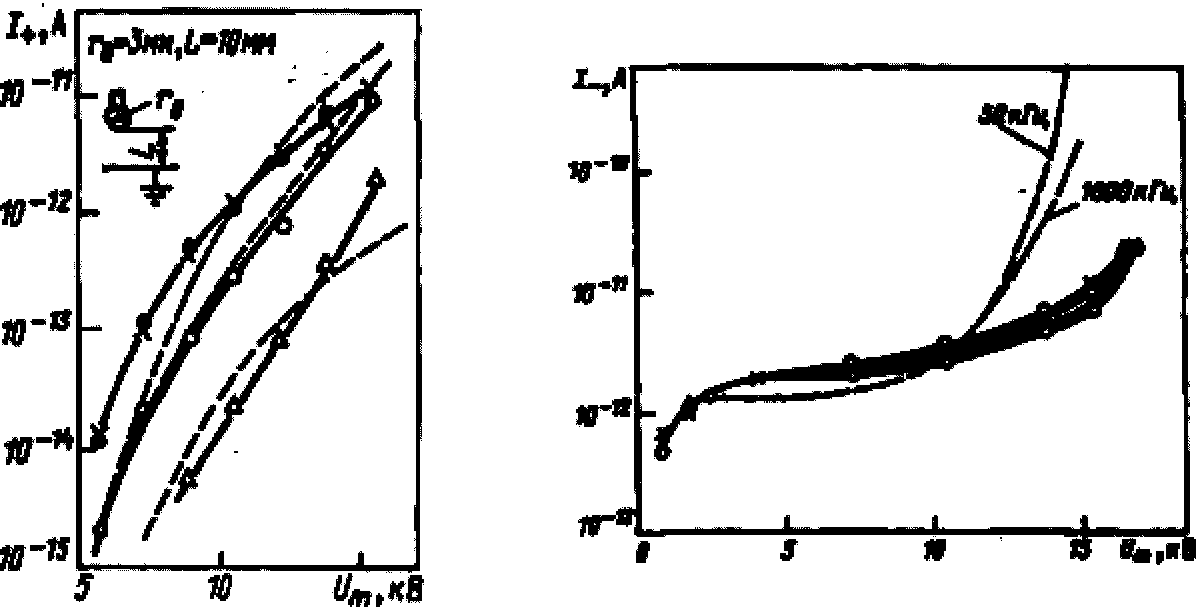
Рис. 1-14. Зависимость тока положительных ионов на коллектор от напряжения ВЧ для разрядного промежутка шар—плоскость. Сплошные кривые — экспериментальные, штриховые — теоретические. Обозначения те же, что и на рис. 1-11
Рис. 1-15. Зависимость тока отрицательных ионов на коллектор от напряжения ВЧ для разрядного промежутка шар—плоскость, r0=3 мм, L0=10 мм. Сплошные кривые — экспериментальные, штриховые — теоретические. Обозначения те же, что и на рис. 1-11
1-6. Влияние объемных зарядов на электрические поля разрядных промежутков
Понятно, что накапливающиеся в разрядном промежутке положительный и отрицательный объемные заряды будут создавать свои «внутренние» электрические поля. Благодаря суперпозиции этих полей с внешним полем, т. е. полем, создаваемым за счет напряжений, приложенного к электродам, создается иная пространственная картина распределения результирующего поля, другими словами, поле искажается. Очевидно, что в результате этого механизм формирования предразрядных процессов и развития самого разряда в значительной степени усложняется. Поэтому при исследовании газового разряда важно уметь рассчитывать искажения электрического поля накапливающимся объемным зарядом. В математическом плане это достаточно сложная задача, так как необходимо знать распределение плотности объемных зарядов в промежутке р+ (х) и р_ (х), которые, вообще говоря, имеют непростую форму, кроме того и распределение внешнего поля, как правило, не является однородным. Поэтому при расчетах результирующего поля в газоразрядном промежутке часто прибегают к тем или иным, оправданным в каждом конкретном случае, физическим приближениям.
Однородные и слабонеоднородные поля.
В этом случае внешнее электрическое поле Е либо вообще одинаково в любой точке разрядного промежутка (Е=U/L), либо, если напряженность электрического поля монотонно убывает от одного электрода к другому, то вдоль центральной силовой линии оно может быть выражено соотношением [15, 16]
(1-11)
где т— показатель степени, характеризующий скорость спада поля; 
— максимальная напряженность внешнего поля у электрода с радиусом кривизны поверхности r0; r — расстояние от центра кривизны электродас радиусом r0 до некоторой точки на центральной силовой линии
. При этом kи вычисляется для различных промежутков по известным соотношениям [15].
Для расчета поля объемного заряда в рассматриваемых конфигурациях обычно применяют следующие упрощения. Если речь идет о диапазоне частот переменного напряжения
, то время пролета электронами всего разрядного промежутка (т.е. время развития лавины) принимается много меньшим периода колебаний напряжения. Таким образом, в указанных промежутках допускается накопление только положительного объемного заряда.
Далее, поскольку заряд, распределенный равномерно по всему объему промежутка, как показано в [17], не способен привести за счет искажения внешнего поля к наблюдаемым снижениям начального напряжения ВЧ разряда, то предполагается, что он накапливается в узком цилиндрическом слое, соосном с центральной силовой линией. Длина этого цилиндра Lи, называемая длиной зоны ионизации, определяется из условия, что в любой точке на его оси αэф>0. В случае однородного поля она совпадает с длиной всего промежутка L, в слабонеоднородных полях Lи<L.
Однако, если распределение р+ (х) от отдельной лавины соответствует экспоненциальному закону, то полагается, что в результате наложения зарядов от серии лавин, проходящих как в отрицательный, так и положительный полупериоды, плотность зарядов выравнивается, т.е.
[16].
Все это приводит к тому, что если воспользоваться уравнением Пуассона для определения поля объемного заряда Ео.з в точке r для промежутка с радиальным полем, то получим простое соотношение:
(1-12)
где φο.з — потенциал поля объемного заряда;
Ф/м.
Решение этого уравнения имеет вид
(1-13)
Окончательно результирующее поле в промежутке в любой точке центральной силовой линии
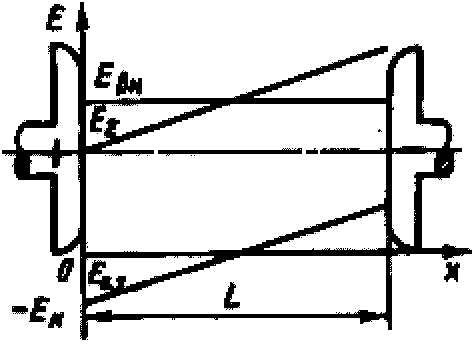
Рис. 1-16. Распределение электрических полей в промежутке плоскость—плоскость: Е — напряженность внешнего поля; Ео.з — напряженность поля накапливающегося положительного объемного заряда; Е∑ — напряженность суммарного поля
Ε∑= Ε + Εо.з. (1-19)
В зависимости от направления внешнего поля (полярности потенциала на рассматриваемом электроде) поле объемного заряда будет по-разному влиять на распределение суммарного поля вдоль центральной силовой линии, что иллюстрирует рис. 1-16 для частного случая однородного электрического поля. Из рисунка видно, что результирующее поле возрастает возле отрицательного электрода и убывает у положительного.
В случае неоднородного поля, наибольшее его значение будет возле электрода с меньшим радиусом кривизны r0 и его усиление полем объемного заряда, очевидно, возможно, когда этот электрод имеет отрицательный потенциал. Таким образом, предполагается, что во всяком случае в слабонеоднородных полях положительный объемный заряд р+ будет приводить к снижению начального напряжения ВЧ разряда по отношению к его значению при постоянном напряжении, именно в отрицательный полупериод. Другими словами, разряд должен возникать именно тогда, когда электрод с меньшим радиусом кривизны имеет отрицательный потенциал [17].
Резконеоднородные поля.
В этом случае отыскание распределения потенциала и напряженности электрического поля при заданной разности потенциалов между электродами и известной плотности объемного заряда с использованием уравнения Пуассона является трудоемкой задачей. Проблема заключается в том, что распределение поля и объемного заряда являются сложными функциями, которые часто невозможно представить в аналитическом виде.
Поэтому большое количество работ посвящено расчету внешнего электрического поля в отсутствие объемного заряда в промежутке [15, 18, 19]. Ряд аналитических решений для распределения поля и потенциала в разрядных промежутках с электродами определенной конфигурации удается получить благодаря преобразованию уравнения Пуассона к разрешимому виду. К таким электродам, например, относятся софокусные параболоиды, концентрические цилиндрические электроды, гиперболоид вращения—плоскость, концентрические сферы и другие. Иногда находятся приближенные решения по методу изображения, когда заведомо известно существование эквипотенциальных поверхностей, например, система двух одинаковых сфер или сфера против плоскости и др. [20].
Как отмечалось выше, много исследований проводится в промежутке острие—плоскость или острие—острие. Для удобства сравнения и обеспечения воспроизводимости результатов измерений форма острия стандартизирована. Острие представляет собой цилиндрический стержень, на конце которого выполнена полусфера того же диаметра (см. рис. 1-17) [21]. В [20] приводится расчет электрического поля для промежутка с электродами указанной конфигурации. Расчет был сделан для случая, когда L/r0>>50. В [21] обсуждается решение уравнения Лапласа путем его сведения к разностным уравнениям, что позволило рассчитать распределение поля в рассматриваемой конфигурации, когда L/r0=10+1. Подробно аналогичная методика расчета поля в промежутке острие—плоскость рассмотрена в [22].
Рис. 1-17. Разрядный промежуток острие—плоскость
Расчету электрических полей в промежутках с резконеоднородным полем при наличии объемного заряда посвящено меньше работ, при этом обычно рассматривается установившаяся фаза электрического разряда [23, 24]. Влияние же поля объемного заряда по мере его накопления на внешнее поле в большинстве случаев рассматривается только на качественном уровне
Одна из попыток количественного расчета поля объемного заряда и его влияния по мере накопления заряда на внешнее поле в промежутке острие—плоскость описана в работах Бесхлебного и Куду [25, 26]. Принцип расчета такой же, как и изложенный выше для слабонеоднородных полей, т.е отдельно вычисляется внешнее поле, и поле объемного заряда, а результирующее поле определяется по формуле (1-19).
Для упрощения расчетов предполагалось, что лавины развиваются вдоль центральной силовой линии, которая в данном промежутке совпадает с его осью симметрии. Поэтому внешнее поле рассчитывалось только на оси промежутка по упрощенной методике [27]:
причем в силу того, что в резконеоднородном поле процессы ионизации имеют место в узкой области возле острия, поле рассчитывалось только в этой ионизационной зоне.
Для учета поля объемного заряда, накапливающегося в промежутке, принята следующая последовательность вычислений. Прежде всего, для данной формы разрядного промежутка, частоты и напряжения, приложенного к нему, вычисляется внешнее электрическое поле на оси промежутка, длина зоны ионизации
, проходимый ионом за четверть периода, по методике, предложенной в [27]. Затем вычисляются зависимость общего числа положительных ионов, создаваемых лавиной Ν+, и радиуса головки лавины rл от проходимого ею пути, и распределение плотности объемного заряда 
вдоль оси промежутка.
После этого можно рассчитать поле этого объемного заряда, или сохранившейся его части, на оси промежутка и вносимые им искажения. По этой же схеме рассчитывается последующая лавина, но все ее параметры вычисляются уже в искаженном результирующем поле промежутка Ε∑ и т.д.
Все количественные оценки проводились только в пределах зоны ионизации по методу численного интегрирования. Для этого вся зона ионизации вдоль оси разрядного промежутка разбивалась на М участков ΔΣ. Коэффициент ионизации вычисляется по формулам [1] и [17]:
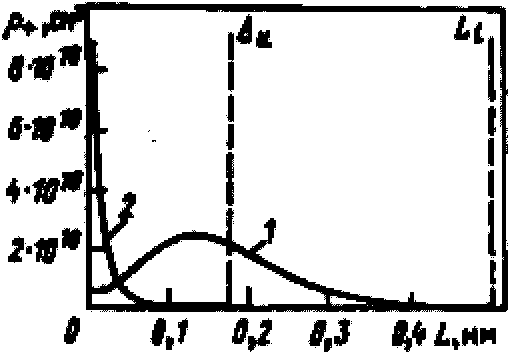
Рис. 1-18. Распределение плотности объемного заряда вдоль осн. разрядного промежутка острие—плоскость от одиночных лавин, прошедших отрицательный (1) и положительный (2) полупериоды
значения соответствующих величин в средней точке k-го участка; Lk — расстояние от поверхности острия вдоль оси промежутка до середины k-го участка; ΔL — ширина участка;
; А и В — некоторые константы по [28]; n0-1 — начальное число электронов, инициирующих лавины; е0 — заряд электрона.
На рис. 1-18 представлены результаты расчета по изложенной методике зависимости плотности объемного заряда
от расстояния до поверхности острия для двух одиночных лавин: лавины, проходящей в момент максимума отрицательного полупериода (-ПП) на острие — кривая 1; и лавины, проходящей в момент максимума положительного полупериода (+ПП) на острие — кривая 2. Расчеты проведены при частоте f, несколько превышающей первую критическую и при напряжении на острие, равном начальному напряжению ВЧ короны. Из этого рисунка видно, что положительный объемный заряд, созданный лавиной в +ПП (кривая 2), практически весь сосредоточен на расстоянии от острия много меньше пути ∆и, проходимого ионом на четверть периода (Т/4) в результате дрейфа в электрическом поле. Это означает, что объемный заряд, оставляемый данной лавиной, спустя Т/2 после его образования, полностью поглотится острием, когда его потенциал станет отрицательным, т.е. накопление р+ от лавин, проходящих в +ПП, в указанных условиях невозможно.
С другой стороны, заряд р+, оставляемый лавиной, проходящей во время -ПП, распределен более равномерно в пределах зоны ионизации. Анализ дрейфа этого объемного заряда после его образования показывает, что та часть ионов, которая располагается на расстоянии 
от поверхности острия в момент прохождения лавины, уже не способна уйти на электроды (если не учитывать рассасывание этого заряда благодаря диффузии и взаимному расталкиванию ионов). Таким образом, в рассматриваемых условиях накопление Р+ происходит за счет лавин, распространяющихся от острия к границе зоны ионизации во время -ПП.
На рис. 1-19 представлена зависимость электрического поля вдоль оси разрядного промежутка от накапливаемого объемного заряда, рассчитанная для этих же условий. Цифры над Кривыми соответствуют порядковому номеру полупериода, начиная с отрицательного. Здесь же, для сравнения, приведено распределение поля от объемного заряда одиночной лавины, прошедшей в +ПП (кривая 2*).
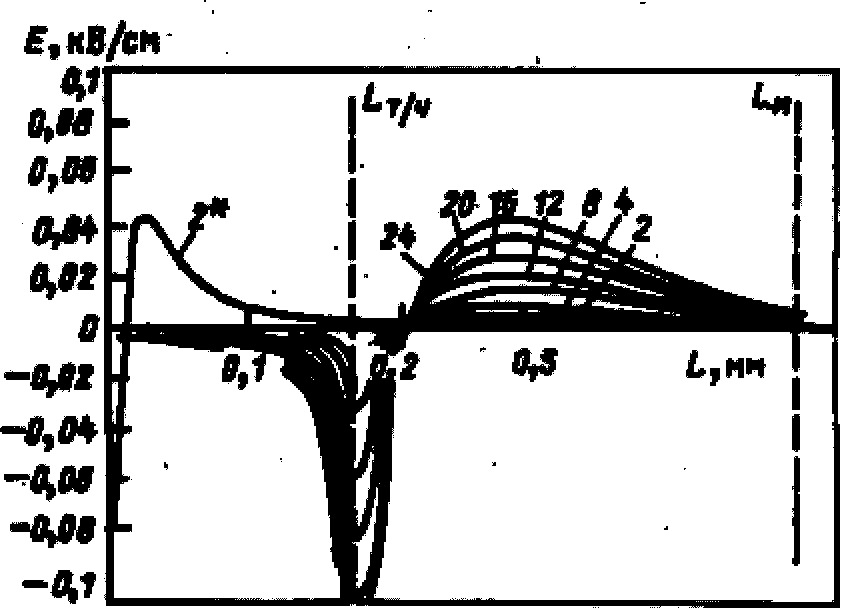
Рис. 1-19. Распределение электрического поля накапливающегося объемного заряда от лавин, проходящих в -ПП, вдоль оси разрядного промежутка
Анализ приведенных зависимостей показывает, что внешнее электрическое поле усиливается полем накапливаемого р+ на участке размером примерно 0,2 мм от поверхности острия в отрицательный полупериод и ослабляется в положительный. В остальной части зоны ионизации, наоборот, оно усиливается в положительный и ослабляется в отрицательный. Такой характер искажения внешнего поля приводит к тому, что в отрицательный полупериод лавины развиваются в усиленном поле и поэтому от периода к периоду становятся все более мощными, а значит нарастает и оставляемый ими положительный объемный заряд.
На основании изложенного может быть предложена следующая модель формирования предразрядного процесса при частоте, превышающей первую критическую [25, 26].
На стадии перехода несамостоятельного разряда в самостоятельный при
в промежутке образуются как положительный, так и отрицательный объёмные заряды.
Электрическое поле Ео.з положительного объемного заряда, накладываясь на внешнее поле Е, усиливает электрическое поле в зоне ионизации в отрицательный полупериод. При этом электрическое поле, создаваемое отрицательным объемным зарядом, в первом приближении не учитывается, так как отрицательный объемный заряд накапливается вне зоны ионизации и распределен в промежутке более равномерно, чем положительный. Роль отрицательных ионов сводится к тому, что они являются поставщиками вторичных электронов для поддержания процесса формирования ВЧ разряда: в положительный полупериод отрицательные ионы втягиваются в область сильного поля и разрушаются в нем, поставляя свободные электроны в зону ионизации (у ее границы). Указанная модель формирования предразрядного процесса позволяет дать удовлетворительное объяснение механизму возникновения разряда, изложенному в главе 2.
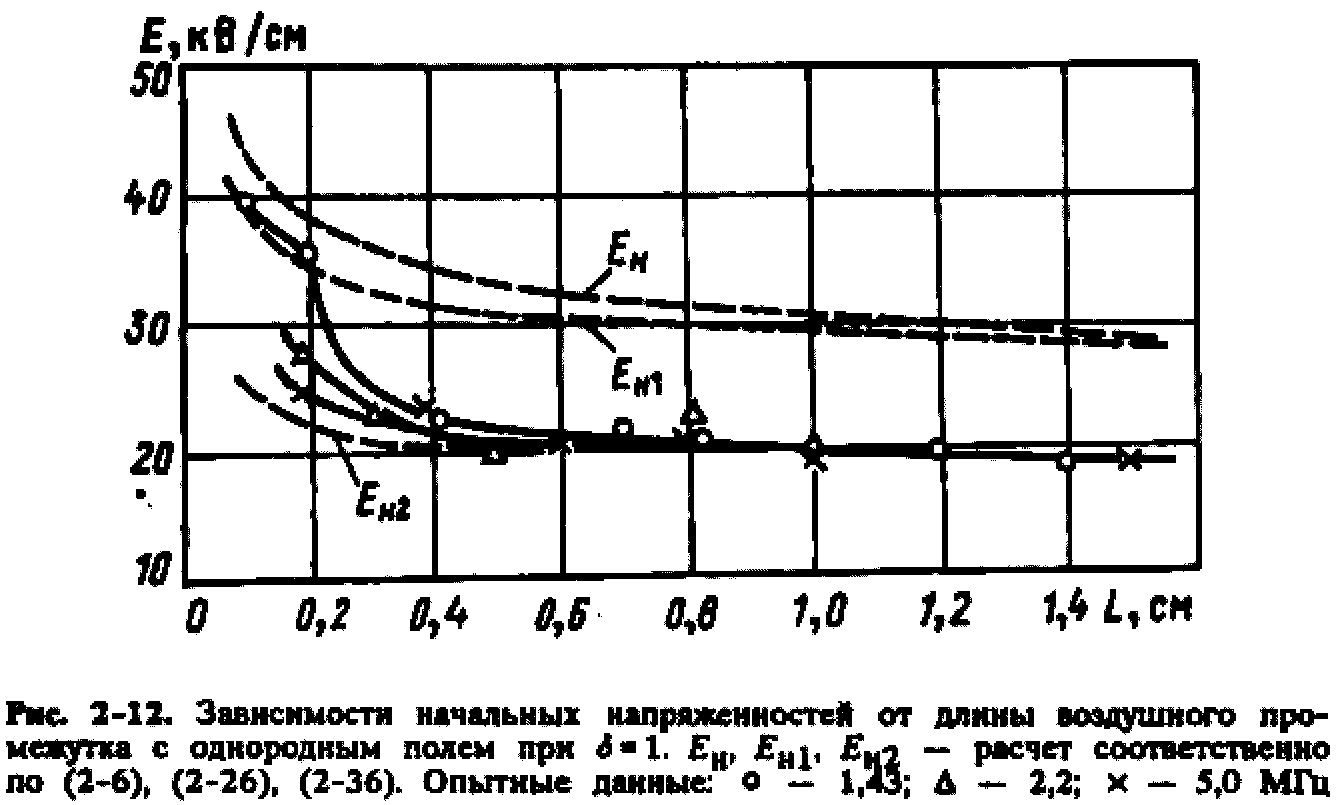
Зависимость начальной напряженности от частоты для промежутка с однородным полем длиной 0,2 см приведена на рис. 2-13. Она иллюстрирует переход от Eн1 к Eн2 c ростом частоты. Достигается он при частотах, составляющих (4—5) fкр2, т.е. достаточно быстро.
Таким образом, для оценочных расчетов можно принять, что для воздушных промежутков с однородным полем
Необходимо отметить, что опытные данные рис. 2-12 и 2-13 получены при δ=1. Поэтому уравнение (2-36) требует проверки при других значениях относительной плотности воздуха.
