Наиболее тяжелым в отношении нагружения корпуса парогенератора является случай, когда система аварийного сброса продуктов реакции обладает минимальной пропускной способностью, т.е. заполнена вытесняемым из контура натрием при продолжающемся истечении воды. С помощью предлагаемой методики определяется равновесное давление в корпусе парогенератора в установившихся режимах истечения воды и выброса натрия при известных гидравлических характеристиках тракта парогенератора и сбросных коммуникаций. При заданном размере разрушения приближенно расход воды в натрий без учета противодавления и испарения в трубке можно рассчитать, используя известные уравнения стационарной гидравлики.
Зная секундный массовый расход воды (или, что то же самое, массовое количество водорода, образующегося в результате реакции в единицу времени), объемный расход натрия ΘNa через сбросные трубопроводы можно записать:
(4.26)
Равновесное давление в корпусе парогенератора р при известных площадях проходных сечений S.; гидравлических характеристиках (ξi, λi, Li, di участков натриевого тракта и давлении на выходе из сбросных линий рс определится из выражения
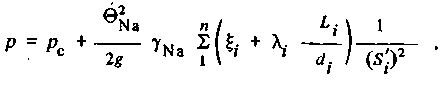(4-27)
Связь между удельной плотностью водорода и его давлением приближенно можно найти из уравнения состояния
(4.28)
Поскольку мы рассматриваем равновесный процесс, происходящий в течение длительного времени, можно принять
Несмотря на то что данный упрощенный метод расчета не учитывает динамики аварийного процесса, значительный запас по расходу воды, завышенное гидравлическое сопротивление сбросных линий в связи с тем, что они считаются с самого начала процесса заполненными натрием, а также учет только одностороннего расширения водорода в сторону компенсационной газовой полости позволяют получить уверенные значения статического давления в корпусе.
Период действия давления будет определяться меньшим из следующих времен:
истечения всего объема воды, заключенного в парогенераторе, с учетом ее аварийного сброса;
выброса всего натрия, заключенного между местом течи и буферной емкостью.
Сравнение расчетных и экспериментальных результатов. Изложенная выше математическая модель нестационарных процессов в натриевом контуре, выполненная с определенными допущениями, требует проверки на предмет сходимости получаемых расчетных результатов с происходящими в действительности явлениями.
Для этой цели были использованы результаты опытов, полученных на экспериментальной установке с вынесенным газовым объемом [44].
Возможные относительные погрешности измерений в экспериментах составляли, %: расхода натрия ±15; давления ±8; температуры ±9; расхода воды в натрий ±15. Инерционность системы измерения расхода и давления в системе магнитный расходомер-осциллограф практически отсутствовала, постоянная времени микротермопар составляла 0,01 с.
На рис. 4.7 и 4.8 в качестве примера представлены результаты экспериментов и расчетов по основным параметрам натриевого контура.
Наибольшее отличие в эксперименте и расчете получено при определении ударного пика в районе корпуса модели. При совпадении длительностей действия (0,001—0,003 с) расчет дает значение в 2—3 раза большее по амплитуде пика давления по сравнению с опытным. Здесь следует, однако, иметь в виду тот факт, что в расчетной модели не учитывается довольно сложный процесс потери энергии ударной волны на деформацию трубного пучка.
Что касается статического давления, развивающегося в натриевом контуре при больших течах воды (а именно это давление важно для определения прочностных характеристик конструкции), то в среднем различие опыта и расчета составляет 20—25%. С учетом погрешности измерений это различие может достигать 30-35%, что, учитывая сложность процессов, можно считать приемлемым для инженерных расчетов.
Пример изменения расчетного и экспериментального расхода натрия по отводящим и подводящим к месту течи участкам контура представлен на рис. 4.8. Сравнение расчетных и опытных результатов показывает, что в целом аналитический метод оценки гидродинамических явлений в натриевом контуре при больших течах достаточно хорошо описывает реальный процесс. Это касается как начального периода, сопровождающегося резким изменением расхода теплоносителя (действие высоких давлений в зоне реакции), так и последующего периода, колебания расхода в котором определяются не только давлением, но и изменением гидравлических характеристик участков натриевого тракта, связанных с заполнением их водородным пузырем. Безусловно, расчетный метод не учитывает дробление водородного пузыря и проскока отдельных его фракций по контуру, а описывает интегральные явления, основанные на использовании ’’поршневой” модели движения водородного пузыря. Отсюда и различие в характерах изменения расчетного и экспериментального расхода Θ в интервале 0,4-0,8 с, когда наблюдается пульсирующее увеличение расхода в опыте и плавное его увеличение при проведении расчета.
Рассмотрим далее, в какой мере результаты расчетного анализа, выполненные по изложенным выше упрощенным методам, отличаются от расчетных величин, полученных по методам с учетом ударных эффектов.
На рис. 4.9 в качестве примера представлены результаты расчета аварийного процесса с учетом сжимаемости натрия и без нее (но с учетом динамики процесса). Видно, что наибольшее различие по давлению в зоне реакции имеет место на начальной стадии процесса после разрушения трубки (0-0,05 с), когда условное давление (рт) несколько меньше давления на корпусе модели, рассчитанного с учетом ударных процессов (рк). При этом разность максимальных статических давлений составляет 20%.
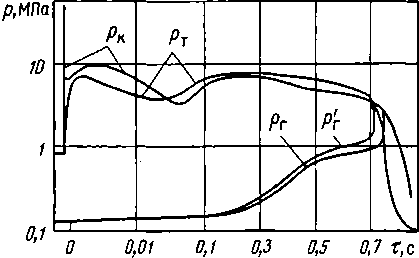
Рис. 4. 9. Расчетное изменение давления на участках натриевого контура с учетом сжимаемости теплоносителя (ρк, рг) и без учета (рт, р'г)
Рис. 4. 10. Расчетное равновесное давление (р) и давление с учетом сжимаемости натрия (рк, рг) в контуре при большой течи
Что касается равновесного аварийного давления в контуре, определяемого по упрощенной методике без учета динамики процесса, то, как видно из рис. 4.10, оно на всем протяжении процесса превышает (на 30-40%) расчетное давление в натриевом контуре (за исключением ударного пика), полученное с учетом сжимаемости теплоносителя.
Особенности анализа аварийных параметров в парогенераторах ’’обратного” типа. Изложенные выше методы расчетных оценок аварийных параметров в циркуляционном контуре при больших течах разработаны и дают удовлетворительную сходимость с экспериментом для условий наиболее распространенных конструкций парогенераторов, когда взаимодействие реагентов происходит в развитом объеме межтрубного пространства. В этих условиях заложенные в расчетную модель предположения об идеальном перемешивании реагентов и практически мгновенной реакции взаимодействия между ними в достаточной мере реализуются на практике.
В конструкции парогенераторов так называемого ’’обратного” типа натрий движется в индивидуальных, изолированных друг от друга в пределах теплообменной поверхности каналах. Примером такого типа может служить парогенератор, где натрий движется внутри теплообменных труб, а вода (пар) - в межтрубном пространстве, а также парогенератор с защитными чехлами, в котором вода движется внутри трубок, и натрий — в кольцевом зазоре между стенкой трубки и стенкой защитного чехла.
При большой течи в конструкции ’’обратного” типа отношение сечения разрушенной трубки к сечению натриевого пространства стремится к единице, в то время как в обычной конструкции это отношение составляет только 10-3— 10-2.
Ограниченный объем в канале должен препятствовать перемешиванию реагентов и полному их взаимодействию, вследствие чего должно происходить постепенное заполнение объёма аварийного теплообменного канала водой с последующим ее поступлением в общие натриевые коммуникации парогенератора (трубопроводы, коллекторы и т. д.).
В связи с этим можно утверждать, что в отношении оценок максимальных гидродинамических эффектов при больших течах в натриевом контуре с ’’обратным” парогенератором представляет интерес процесс не в аварийном канале, а в соединительных конструкциях (камерах, коллекторах), причем достаточно развитые объемы последних позволяют применять для этих оценок изложенные выше методики.
Однако очевидно, что интенсивность процессов взаимодействия в коллекторе будет зависеть (особенно в начальный момент) от режима движения воды через аварийный канал (трубку). При этом для оценки режима требуется рассмотреть процесс внедрения воды в канал с учетом незавершенности реакции взаимодействия между реагентами в полости трубки, а также влияние таких факторов, как скорость разрушения канала, интенсивность взаимодействия, гидравлическая характеристика канала на процесс истечения воды в коллектор.
В соответствии с изложенным выше была разработана модель процесса и расчетным образом показано влияние каждого из факторов в достаточно широком диапазоне их изменения [43]. В модели полагается, что при разрушении канала (трубки) по заданному закону до момента перекрытия водородным пузырем сечения канала τпер взаимодействие натрия и воды идет мгновенно и описывается уравнениями, характерными для процесса в развитом объеме (см. выше). При этом интенсивность взаимодействия определяется только скоростью разрушения. Как только водородный пузырь перекрывает все сечение разрушенного канала, между реагентами образуется водородная прослойка и взаимодействие попадающей в канал воды с натрием может проходить двумя путями:
за счет контакта с натрием, остающимся на внутренней стенке в процессе вытеснения теплоносителя из аварийного канала;
за счет массообмена между реагентами, разделенными продуктами реакции.
При этом из-за разности давлений между натрием и водой происходит движение системы вода-водородный пузырь-натрий вдоль канала в сторону коллектора, а объем пузыря увеличивается за счет расширения и в результате указанных двух видов взаимодействия.
Расчетный алгоритм, описывающий движение натрия, воды и водорода внутри поврежденного канала, может быть составлен с использованием уравнений нестационарной гидродинамики.
Наибольшие сложности при составлении расчетного алгоритма встречаются при описании процесса взаимодействия воды и натрия внутри аварийного канала.
Уравнение для расчета массы водорода в пузыре при указанном выше двойном механизме взаимодействия можно представить в виде
(4.31)/
Количество водорода, образующегося в результате контакта воды с натрием на поверхности канала МNa пл, определяется толщиной слоя и длиной столба воды, внедрившегося к данному моменту в канал.
Точный расчет взаимодействия реагентов за счет массообмена практически невозможен из-за сложности учета всех процессов, связанных с переносом массы в условиях турбулентного перемешивания и диффузии с одновременным наличием химической реакции. Однако в общем виде количество воды, прореагировавшей при массообмене реагентов через водородную прослойку в канале, можно представить следующим образом [49]:
(4.32)
В этом уравнении суммарный коэффициент массообмена D включает в себя турбулентную Dт и диффузионную Dд составляющие.
Принимая линейное распределение концентрации воды вдоль объема переноса, уравнению (4.32) можно придать в конечных разностях следующий вид:
(4.33)
Для оценки минимального значения коэффициента массопереноса воспользуемся экспериментальным значением коэффициента концентрационной диффузии воды в водороде, которое согласно [50] с учетом поправок на давление и температуру, характерных для парогенераторов типа натрий-вода, равно 0,5 · 10-5 м2/с.
Безусловно, наличие турбулентного массообмена будет увеличивать суммарный коэффициент по отношению к его минимальному значению.
Были выполнены расчеты для вертикального канала в виде трубки диаметром 16 х 2,5 мм с расстоянием от места разрушения до коллектора 10 м. Давление в натриевой полости 0,3 МПа, в пароводяной 14,0 МПа. Время разрушения трубки до полного сечения 10-5 с.
Анализ показывает, что при фиксированной толщине пленки натрия на стенке канала (0,1 мм) рост коэффициента массообмена даже на пять порядков по отношению к выбранному минимальному значению увеличивает долю прореагировавшей воды к моменту выхода ее в коллектор только на 0,08%. В то же время изменение толщины пленки от 0,1 до 1 мм увеличивает долю прореагировавшей с натрием воды с 2,4 до 21%, что указывает на подавляющее преобладание ’’пленочного” взаимодействия над Массопереносом.
Более существенное влияние на начальный расход воды в коллектор (а именно эта величина нас интересует при оценке аварийной ситуации и контуре) оказывает скорость разрушения трубки. Так, увеличение времени раскрытия трубки до полного сечения с 10-5 (мгновенного) до 5 с приводит к уменьшению начального расхода с 3 до 1,75 кг/с. Здесь сказываются эффекты, связанные с гидравлическим сопротивлением места разрушения. Следует отметить, что при большом перепаде давлений между натриевой и пароводяной полостями, характерном для парогенератора типа натрий—вода, процессы перекрытия сечения трубки водородным пузырем, вытеснения водорода, а затем и воды в коллектор довольно скоротечны и завершаются менее чем за 1 с при времени раскрытия трубки до полного сечения в диапазоне 1·10-5 — 5 с.
Таким образом, при определении начального режима истечения воды в натрий при больших течах в парогенераторах ’’обратного” типа целесообразно учитывать влияние скорости разрушения канала, а из рассмотренных двух механизмов взаимодействия реагентов достаточно учитывать только контакт с пленкой натрия.
Анализ также показал, что возникновение аварийных динамических явлений внутри канала (пиков давления) при больших течах влияет главным образом на режим внедрения в канал воды и не выдвигает дополнительных требований к прочности теплообменных трубок.
