Приложение 3. Структура погрешностей расчета потерь электроэнергии по числу часов наибольших потерь
Методическая погрешность расчета потерь с использованием т состоит из двух составляющих: погрешности определения τ различными приближенными способами по сравнению с точным его значением, расчитываемым по графику, и погрешности расчета потерь электроэнергии по точно определенному значению т. Первая составляющая исследована в приложении 2. Вторую составляющую назовем погрешностью неадекватности. Она обусловлена тем, что в сложной сети графики нагрузки каждой ветви в общем случае различны, т же может быть определено лишь как одно общее значения для всей сети. Это связано с отсутствием на практике информации о графиках нагрузки большинства линий и их резкой зависимостью от режима в замкнутых сетях.
В этом случае единственными графиками, которые в той или иной степени характеризуют потери электроэнергии в питающих сетях, являются графики суммарной нагрузки системы. Погрешность неадекватности равна нулю лишь в частном случае определения потерь электроэнергии в одной ветви при известном графике ее нагрузки и постоянства напряжения в том из ее узлов, график нагрузки которого известен.
В общем случае погрешность неадекватности обусловливается следующими причинами:
- определением τ по графикам суммарной нагрузки энергосистемы, включающим в себя как нагрузки узлов, так и потери в сетях:
(П3.1)
Так как потери являются квадратичной функцией нагрузки, то график будет более пиковым и, следовательно имеющим меньшее
значение т, чем график.
Поэтому определение т по графику суммарной нагрузки системы всегда будет давать отрицательную погрешность. При этом погрешность будет тем больше, чем выше уровень потерь мощности в режиме наибольших нагрузок и чем меньше число часов их использования;
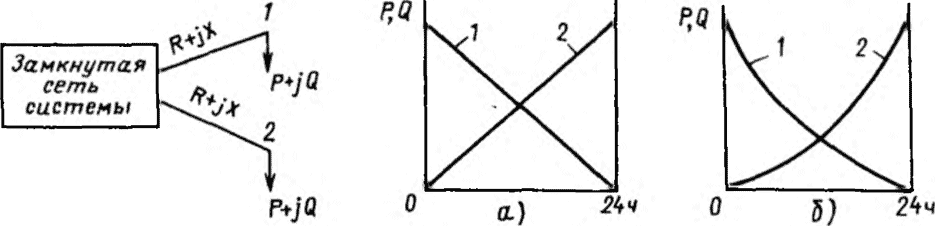
Рис. П3.1. Условная схема замкнутой и радиальных сетей системы
Рис. П3.2. Идеализированные графики нагрузки узлов схемы рис. П3.1
- внутрисуточной неоднородностью графиков нагрузки различных узлов. Наличие в системе нагрузок с графиками различной конфигурации приводит к выравниванию суммарного графика и, следовательно, увеличению т. В этом случае вносится положительная погрешность. Так, при определении с помощью т потерь электроэнергии в ветвях 1 и 2 системы (рис. П3.1) при идеализированных графиках нагрузки, изображенных на рис. П3.2, а, погрешность достигает 50%, а при графиках, соответствующих рис. П3.2, б, - 67 %. В замкнутых сетях внутрисуточная неоднородность графиков нагрузки не приводит к таким большим погрешностям и при близком расположении узлов с неоднородными нагрузками может быть и отрицательной.
Рис. П3.3. Идеализированные лучевая (а) и цепочечная (б) схемы
Кроме того, реальные графики нагрузок не являются столь неоднородными, как это показано на рисунках. Однако и при этих обстоятельствах погрешность может оставаться значительной;
- сезонной неоднородностью изменения нагрузок, обусловленной изменениями в структуре потребления каждого узла системы. Неучет сезонной неоднородности может приводить как к положительной, так и к отрицательной погрешности.
Естественно предположить, что значения погрешностей зависят также и от особенностей построения схемы сети. Поэтому кроме выборки схем реальных сетей энергосистемы исследовались схемы, погрешности определения потерь в которых являлись крайними границами значений погрешностей. Такие схемы представлены на рис. П3.3. В схеме П3, 3, а отсутствуют участки, общие для нагрузок различных узлов. В схеме рис. П3, 3, б, напротив, нагрузки ветвей максимально зависят от соотношения нагрузок узлов. Схема рис. П3.3, б наиболее близка к схемам распределительных сетей 6—10 кВ; схемы питающих сетей системы являются некоторыми средними между приведенными на рисунках. Анализ показал, что и погрешности неадекватности для замкнутых сетей находятся в интервале погрешностей, соответствующих приведенным схемам. Для большей определенности анализа предполагалось, что сечения проводов выбраны по экономической плотности тока и нагрузки распределены равномерно по сети.
Результаты расчетов более 300 вариантов, различающихся сочетанием графиков различных конфигураций по трем реальным схемам и двум схемам, приведенным на рис. П3.3, показали, что погрешность неадекватности имеет систематическую составляющую, приводящую к завышению потерь в среднем на δ = 6%, и среднеквадратичное отклонение Δ = 6,5 %.
Использование для расчета г формулы (П2.3) в области кз > 0,3, соответствующей графикам суммарной нагрузки энергосистем и центров питания разомкнутых сетей 35-150 кВ, дает отрицательную систематическую погрешность около 4% и среднеквадратичное значение погрешности тоже около 4%. Результирующая погрешность расчета потерь с использованием формул (1.17) и (1.18) содержит систематическую составляющую δ = 6-4 = 2 % и случайную 
= 7,6%. Поэтому для получения интервала неопределенности потерь необходимо расчетное их значение умножать на коэффициент коррекции кк=100/102=0,98 и к этому значению относить интервал ± 15,2%.