Стационарное тепловое поле электрических машин описывается уравнениями Лапласа или Пуассона и может моделироваться как методом сплошных сред, так и методом электрических сеток. При моделировании теплового поля может использоваться четыре системы аналогий. Первая система аналогии, согласно которой расходу тепла Q соответствует ток в модели I, перепаду температур ∆t — напряжение в модели U и тепловому сопротивлению RT — в модели омическое сопротивление R, является в данном случае наиболее удобной.
Омическая сетка сопротивлений также является наиболее удобной и простой при моделировании тепловых процессов в электрических машинах.
Пассивная электрическая цепь может быть применена при моделировании системы линейных алгебраических уравнений со следующими ограничениями:
1) главные коэффициенты матрицы должны быть больше или равны сумме побочных
![]()
- побочные коэффициенты матрицы отрицательны
![]()
- коэффициенты системы симметричны
![]()
Иными словами, пассивные электрические цепи могут быть применены для моделирования тепловой схемы электрической машины без учета подогрева охлаждающего воздуха и без учета зависимости потерь в обмотках от температуры. Учет подогрева воздуха и зависимости потерь от температуры может осуществляться в этом случае по методу последовательных приближений. Модель, работающая на основе пассивной сетки сопротивлений, и методы работы на ней описаны в [Л. 59].
Для учета зависимости потерь в обмотках от температуры при моделировании необходима компенсация главных коэффициентов, которая может быть осуществлена применением положительной обратной связи в источниках тока, питающих узлы схемы.
Главные коэффициенты матрицы, как отмечалось в § 3-2, состоят в этом случае из трех частей
![]()
Для моделирования такой матрицы, если αk0<P0at, использовать пассивную электрическую цепь и обычные источники тока нельзя. Если перенести третий член в правую часть уравнения, то оставшуюся матрицу можно моделировать обычной пассивной цепью, а правые части в виде Pk0+Pk0at задавать источниками тока с положительной обратной связью.
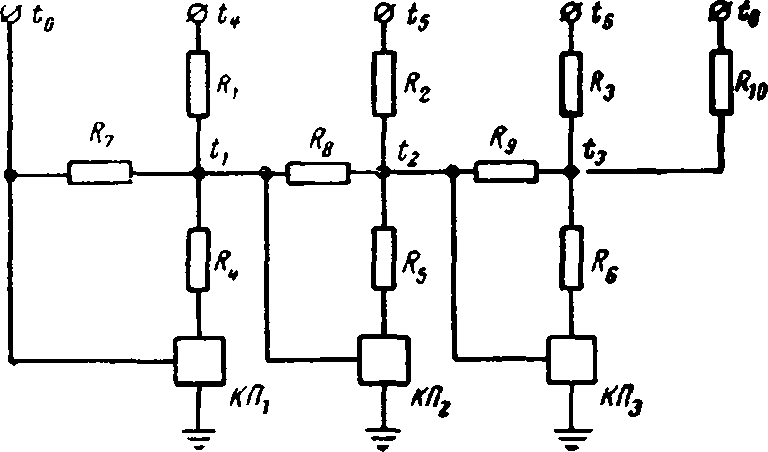
Рис. 3-5. Схема моделирования подогрева воздуха в межреберном канале электродвигателя на модели-аналоге.
R1, R2, R3 — сопротивления, соответствующие теплоотдаче с поверхности;
= R8=R9=R10≈∞ — сопротивления, соответствующие теплопроводности воздушной струи; КП1, КП2, КП3 — «катодные повторители».
Модели, работающие на этом принципе, описаны в [Л. 14 и 27]. В обеих моделях в качестве источника тока использованы пентоды. Модель по [Л. 14] работает на постоянном токе и требует подстройки величины а в зависимости от Рk0. Модель по [Л. 27] работает на переменном токе и не требует подстройки а при изменении Рk0. Настройка а осуществляется один раз при настройке модели и впоследствии при работе не изменяется. Использование переменного тока в этой модели позволило значительно упростить ее схему и избавиться от дрейфа нуля источников тока, который имеет место при использовании для источников тока усилителей постоянного тока.
Модель по [Л. 27], разработанная в институте Гипронисэлектрошахт, позволяет, кроме этого, моделировать и подогрев охлаждающего воздуха, т. е. систему, описываемую алгебраическими уравнениями с несимметричной матрицей коэффициентов.
Моделирование несимметричной матрицы осуществляется следующим образом.
В системе уравнений
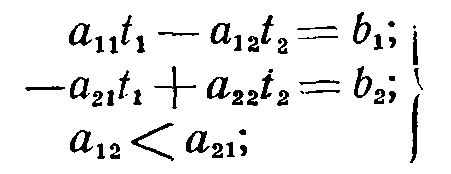 (3-6)
(3-6)
представим член α21, состоящим из двух составляющих
![]() (3-7)
(3-7)
Подставим значение (3-7) в (3-6)
![]() (3-8)
(3-8)
Выделим член Δα21t1 в дополнительный узел с температурой t3
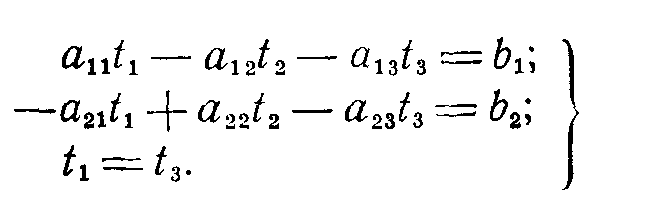
(3-9)

Рис. 3-6. Блок-схема модели-аналога.
Первые уравнения моделируются сеткой сопротивлений, так как имеют симметричную матрицу. Условие t3=t1 выполняется с помощью специального усилителя с глубокой отрицательной связью, имеющего свойства катодного повторителя, т. е. очень большое входное сопротивление и малое выходное. На рис. 3-5 приведена схема моделирования. Блок-схема модели, разработанной на основе указанных принципов моделирования, приведена на рис. 3-6.
Модель состоит из коммутатора 1 на 40 узлов, 30 ячеек задачи токов 2, 80 блоков сопротивлений 3, 12 образцовых сопротивлений 4, 20 усилителей для моделирования подогрева воздуха 5, измерительного устройства 6, задающего генератора 8 для питания модели на 820 гц (модель работает на переменном токе) и блока питания 7. Модель собрана в металлическом корпусе с размерами 1482x1520x830; общий вид ее приведен на рис. 3-7.
Работа на модели сводится к набору на коммутаторе задачи, установки необходимых значений сопротивлений и токов, величина которых определяется по значениям сопротивлений схемы, потерям в узлах и масштабу моделирования.

Рис. 3-7. Общий вид модели-аналога.
Модель имеет постоянный масштаб по температуре: 10 в. в модели соответствуют 100° С в натуре. Масштаб потерь (токов) выбирается исходя из максимального тока источника, который в данной модели не должен превышать 3,5 ма, и максимального значения сопротивления, которое не должно превышать 20 ком. Величина потерь в обмотках берется при окружающей температуре 40°С, т. е. для холодной машины. В источниках, моделирующих потери в обмотках, включается положительная обратная связь по току.
В результате расчета получаем не только превышения температуры различных узлов, но и потери в обмотках, соответствующие этим температурам. Модель позволяет моделировать тепловые схемы, описываемые 40 однородными алгебраическими уравнениями, из которых 30 с правой частью и с несимметричной матрицей при числе несимметричных коэффициентов не более 20.
Описанная модель является одним из наиболее универсальных устройств для тепловых расчетов электрических машин, так как позволяет автоматически учитывать как зависимость потерь в обмотках статора от температуры, так и охлаждение и нагрев охлаждающих агентов, что особенно важно для крупных машин с внутренней циркуляцией воздуха. Эта модель позволяет анализировать тепловые поля не только электродвигателя в целом, но и в отдельных его конструктивных элементах, что может быть использовано для составления методики расчета отдельных сопротивлений. Кроме того, модель может быть использована для решения инверсной задачи, т. е. определения сопротивлений, а также для теплового расчета и анализа трансформаторов и электрических аппаратов.
Точность решения уравнений можно определить из результатов расчета электродвигателя АНВ-13-62-4 на модели и на машине «Минск-1» (табл. 3-3). Из табл. 3-3 видно, что погрешность расчета на модели не превышает 2—3%, что вполне приемлемо для тепловых расчетов. Точность тепловых расчетов зависит от погрешностей вносимых конечно-разностной аппроксимацией дифференциальных уравнений, т. е. замены их алгебраическими уравнениями, от количества тел, на которые расчленяется машина, от машинной погрешности расчета системы уравнений, описывающих тепловой процесс, от погрешности расчета греющих потерь и тепловых сопротивлений электрической машины.
Погрешности конечно-разностной аппроксимации и допустимые величины размеров участков тел схем замещения освещены в [Л. 4, 31 и 59].
Машинная погрешность расчета на ЭЦВМ составляет десятые доли процента, на моделях-аналогах — единицы процентов.

