Проверка принципов идентификации параметров ВЛ.
Для проверки принципов предложенных решений произведен расчет однофазного короткого замыкания, результаты которого рассмотрены, как исходные данные для идентификации параметров. Две смежные ВЛ (рис. П.1.) напряжением 330 кВ представлены в распределенных параметрах. Изучаемая ВЛ длиной L = 160,6 км имеет следующие удельные параметры нулевой последовательности,


Некоторые отклонения от исходных расчетных данных объясняются несовершенством схем замещения ВЛ. Наконец, итерационный метод с использованием программы минимизации функции (2.7) и представления ВЛ в распределенных параметрах, как функций искомых величин, реализуется следующим образом. Удельные параметры ВЛ: ![]()
Узловые проводимости ВЛ:
![]()

Результат практически совпадает с исходными данными и говорит о том, что при фиксации токов и напряжений в виде абсолютных величин и углов можно определять все три основных параметра ВЛ.
Определение параметров ВЛ на основе данных регистратора аварийных событий.
Рассматривается предыдущая ВЛ, но на основе реальных электрических величин. При внешнем коротком замыкании одной фазы на смежной ВЛ 330 кВ зарегистрированы следующие величины нулевой последовательности (утроенные значения): на ПС 87: U87=211,95 кВ, I87=0,7344 кА, на ГЭС9: U9=29,74 кВ, I9=0,7779 кА. Длина ВЛ L=166.6 км. Замечаем, что углы между напряжениями регистраторами не определяются. Используя методику приложения 1 и эти данные получаем:

Расчетная величина удельного реактивного сопротивления при глубине возврата тока через землю 1000 м, рассчитанная по методике [8], дает величину х=1,162 Ом на км. Опыт искусственного КЗ при подаче пониженного напряжения на этой ВЛ дал увеличение реактивного сопротивления почти на 30% к расчетному, что хорошо согласуется с сопротивлением, полученным на основе данных регистратора. Объясняется такое увеличение прохождением этой ВЛ по скалистым грунтам с глубиной возврата тока прядка 6000 м.
Определение параметров ВЛ, связанной взаимоиндукцией.
Две ВЛ длиной 109 км каждая, следующие в одной трассе, связаны взаимоиндукцией на всем протяжении (рис. 2.3). ВЛ, параметры которой интересуют, напряжением 330 кВ (концы обозначены “а”, “b”, вторая ВЛ напряжением 220 кВ (концы обозначены “с”, “d”). При внешнем КЗ на землю на смежной ВЛ произведен расчет однофазного короткого замыкания и на интересующей ВЛ 330 кВ зарегистрированы следующие электрические величины нулевой последовательности: Ua=253.187, Iа=![]()
![]() .
.
Все напряжения в кВ, токи в кА. Расчеты проведем различными способами и сравним результаты.
Алгоритм итерационного метода строится следующим образом.
Принимается, что активная составляющая удельного сопротивления известна и равна «г», тогда искомыми величинами являются х - удельное реактивное сопротивление, b- удельная емкостная проводимость, т - удельное сопротивление взаимоиндукции.
Путем минимизации функции (10) определяются эти три удельные величины: «х», «b» и «m», соответственно принимаются: zab(x)=0.205+jx, ![]() . Затем в полном соответствии с [18] строится матрица узловых проводимостей этих двух параллельных ВЛ: Yabccb(x,b,m), токи ВЛ находятся как:
. Затем в полном соответствии с [18] строится матрица узловых проводимостей этих двух параллельных ВЛ: Yabccb(x,b,m), токи ВЛ находятся как:
![]()
В данном случае в функции (10) используются только токи первой ВЛ 330 кВ (Iа и А). В результате получаем:

практически совпадающие с исходными.
Использование формулы (2.1), в которой напряжения корректируются согласно (2.12) дает:
z = 0.206 + j1.253,
использование формул (2.5), также с коррекцией напряжений дает следующие значения параметров:
![]()
Появление активной составляющей в проводимости является в данном случае следствием несовершенства П-образной схемы замещения ВЛ, однако, она на два порядка меньше реактивной, такой величиной вполне можно пренебречь. Остальные величины, определенные разными способами отличаются друг от друга несущественно.
Алгоритмы и примеры расчета матрицы узловых проводимостей группы ВЛ, связанных взаимоиндукцией.
Знание этих алгоритмов необходимо для составления алгоритма идентификации параметров ВЛ, связанных взаимоиндукцией и представленных в распределенных параметрах. Алгоритмы составлены и расчеты проведены с использованием комплекса математических программ «Mathcad» для ВЛ, представленных в распределенных параметрах. Все электрические параметры, а также токи и напряжения нулевой последовательности.
Алгоритм и расчет матрицы узловых проводимостей двух ВЛ, связанных взаимоиндукцией.
Две ВЛ, связанные взаимоиндукцией (см. рис. 2.3). Расчет проведен в полном соответствии с алгоритмом, изложенным в [18].



где индексы пробегают значения: ζ = 1, 3, 5, у = 2, 4, 6.
Дифференцируя первое уравнение по х второй раз, подставляя в него второе уравнение и перенося правую часть в левую, получаем основное дифференциальное уравнение второго порядка:

решение которого, например с помощью функции «root», в программе Mathcad, дает шесть корней, которые в свою очередь позволяют записать решение для напряжений и токов:

(П.4)
где А, В, С - постоянные интегрирования. Далее задача заключается в том, чтобы связать напряжения и токи через постоянные интегрирования и последние исключить, оставив матрицу связывающую токи и напряжения в начале и конце ВЛ, которая и будет являться искомой матрицей проводимости. Всего имеется 18 постоянных интегрирования. Физические соображения дают следующие граничные условия:
 (П.5)
(П.5)
Для исключения постоянных интегрирования необходимо выразить постоянные В и С через А. Для этого реализуем следующую операцию. Дважды продифференцируем уравнение (11.4) и результат подставим в (11.2). Новое уравнение распадается на три зависимости, каждое из которых распадается на шесть групп по признаку e. Ввиду линейной независимости этих групп каждая из них может быть приравнена нулю. Из последних уравнений компонуются труппы уравнений потри в каждой по вышеупомянутому признаку. Например, для r3 получается система уравнений:
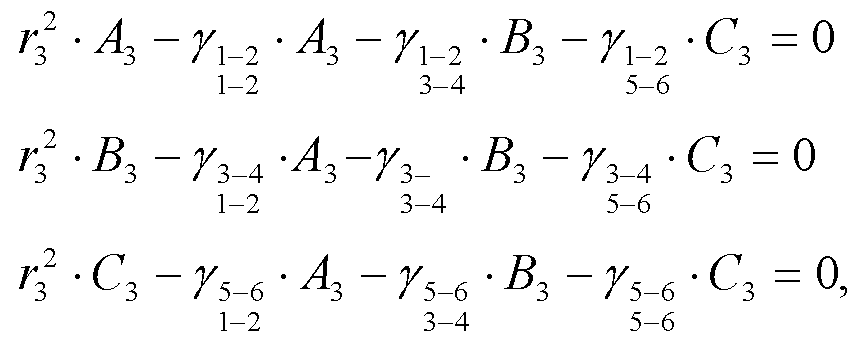
где использованы элементы γ в соответствии с (11.2А).
Из этих уравнений следует следует:

Проделав аналогичные операции для всех значений корней характеристического уравнения, получаем обобщенные зависимости:

(П.6)
На следующем этапе преобразуем зависимости (П.5) следующим образом. Объединим напряжения в одну матрицу-столбец, все постоянные интегрирования выразим через А и представим в матричной форме:

Аналогичное преобразование выполним и для токов:

(П.8)
Теперь появляется возможность исключить постоянные интегрирования Аi и найти матрицу проводимостей трех ВЛ связанных взаимоиндукцией:
![]() (П.9)
(П.9)
ЛИТЕРАТУРА
- Угримов Б.И. 50 лет трехфазного тока // Электричество. 2004. №10
- Веников В.А., Шнейберг Я.А. От истоков электропередачи к прогнозам на будующее//Электричество. 1983. №11.
- Беляков Ю.С. История расчетов аварийных режимов в XX века // Сто лет релейной защите - СПб.: ПЭИПК 2011.
- Кессельринг Ф. Селективная защита. - М - Л.: Энергоиздат, 1932.
- Вагнер К.Ф., Эванс Р.Д. Метод симметричных составляющих. - Л-М.: ОНТИ, 1936.
- Вагнер К.Ф., Щедрин Н.Н. Метод симметричных составляющих и применение к расчету аварийных режимов - Л-М.: ОНТИ, 1933
- Щедрин Н.Н. Токи короткого замыкания высоковольтных систем - М.: ОНТИ, 1935.
- Ульянов С.А. Электромагнитные переходные процессы в электрических системах. - М-Л.: Энергия, 1964.
- Руководящие указания по релейной защите. Вып.11 Расчеты токов короткого замыкания для релейной защиты и системной автоматики в сетях 110-750 кВ. - М.: Энергия, 1979.
- Мельников Н.А. Электрические сети и системы. - М.: Энергия, 1969.
- Лыкин А.В. Электрические системы и сети. - Новосибирск: 2003.
- Аржанников Е.А., Чухин А.М. Автоматизированный анализ аварийных ситуаций энергосистем. - Μ.: НТФ «Энергопресс», 2000. - (Библиотечка электротехника - приложение к журналу «Энергетик»),
- Пуляев В.И., Усачев Ю.В. Цифровые регистраторы аварийных событий энергосистем. - М.: НТФ «Энергопресс», 1999. - (Библиотечка электротехника - приложение к журналу «Энергетик»),
- Алюнов А.Н., Бабарушкин В.А., Булычев А.В. Уточнение параметров модели электрической сети по данным регистраторов аварийных режимов // XV научно- техническая конференция «Релейная защита и автоматика энергосистем 2002». - М.: 2002.
- Брацлавский С.Х., Гершенгорн А.И., Лосев С.Б. Специальные расчеты электропередач сверхвысокого напряжения. -М: Энергоатомиздат, 1985.
- Дьяконов В. Mathcad 8/2000: специальный сборник. - СПб.: Питер, 2000.
- Неклепаев Б.Н. Схемы замещения нулевой последовательности параллельных линий большой длины//Электричество. 1962. №6.
- Беляков Ю.С. Расчет взаимоиндукции длинных линий электропередачи// Электричество. 1997. №11.

