ЛЕКЦИЯ 2. Вопросы идентификации параметров ВЛ.
Параметры ВЛ играют значительную роль в расчете всех режимов электрических систем. В некоторых случаях, таких как определение мест повреждения ВЛ, расчеты уставок релейной защиты, их значение особенно велико. Анализ параметров ВЛ был произведен в главе 1. Напомню, что к основным параметрам ВЛ следует отнести следующие:
- длина ВЛ в км [L],
удельное комплексное сопротивление прямой и обратной последовательности в Ом/км [zl],
удельная емкостная проводимость прямой и обратной последовательности в Сим/км [yl],
- удельное комплексное сопротивление нулевой последовательности в Ом/км [zθ],
-удельная емкостная проводимость нулевой последовательности в Сим/км [y0],
- удельная величина комплексного сопротивления взаимоиндукции рассматриваемой ВЛ с каждой параллельно следующей и последних между собой в Ом/км [mi-jp-q, j>i- индексы изучаемой ВЛ, p>q- индексы остальных ВЛ].
Во введении было упомянуто о двух вариантах идентификации электрических параметров ВЛ. Первый связан с опытом искусственного короткого замыкания, при котором ВЛ замыкается накоротко на одном конце и подается пониженное напряжение на другом конце ВЛ. Основной недостаток - трудности организационного характера. Возможно также, что пониженное подаваемое напряжение обуславливает погрешность определяемых параметров за счет их нелинейности, проявляющейся при малых токах. Наконец, в этом случае становится неопределенным влияние взаимоиндукции и определение ее параметров. Второй вариант реализуется благодаря грозовым явлениям и другим источникам коротких замыканий. Современные системы регистрации аварийных процессов [12], [13] позволяют получить данные о токах и напряжениях как самой поврежденной ВЛ, так и о токах и напряжениях смежных с ней элементов электрической системы. Кроме того, преимуществами второго варианта являются: возможность повторяемости опытов, следовательно, накопление статистических данных о параметрах, а также определение параметров при протекании токов короткого замыкания, т.е. тех токов, при которых эти параметры должны работать.
Использование аварийных данных поврежденной ВЛ для определения ее параметров требует сведений о месте повреждения, характере повреждения и величине переходного сопротивления в месте повреждения. Поэтому предпочтительным является использование аварийных данных при внешнем коротком замыкании. Дальнейшее рассмотрение будет проведено для этого случая.
Есть сведения о решении поставленной задачи в упрощенном варианте в [14]. Уточненные варианты идентификации параметров ВЛ практически не рассматривались.
1. Идентификация параметров одиночных ВЛ.
Для схемы, изображенной на рис. 2.1, искомое удельное сопротивление определяется по формуле:
 (2.1)
(2.1)
В этой формуле Ua и Ub должны быть комплексы напряжений зафиксированных по концам ВЛ, Lа-b - комплекс тока ВЛ, L- длина ВЛ, z- комплексное продольное удельное сопротивление ВЛ. Не представляет труда определение комплекса тока, поскольку современные регистраторы [12], [13] фиксируют абсолютную величину тока и его угол относительно напряжения. Для векторов напряжений также важно знать угол между ними, но именно этот угол не определяется просто. Теоретически определение этого угла возможно путем сопряжения записей аварийных процессов, полученных по концам ВЛ с поправкой на время распространения электромагнитной волны с одного конца ВЛ к другому. Возможен вариант с использованием единой системы астрономического времени. Однако оба эти варианта пока трудно реализуемые. Не исключается и может оказаться полезным вариант использования расчетной величины угла. На практике применяют модули напряжений и токов, при этом учитывают, что активная составляющая комплексного сопротивления определяется расчетом достаточно точно даже для составляющих нулевой последовательности [8]. По модулю полного удельного сопротивления и его активной составляющей легко находится индуктивная составляющая. В формуле (2.1) и далее не будет вводиться специальное обозначение комплексной величины, поскольку, в зависимости от представления поступивших данных, величины могут быть как комплексными, так и не комплексными, при этом все формулы справедливы для обоих случаев. Кроме того, формула (2.1) справедлива как для определения параметров прямой и обратной последовательности, так и нулевой (подставляются составляющие соответствующих последовательностей). Кстати, для определения параметров прямой последовательности нет необходимости ждать аварийной ситуации, достаточно зафиксировать токи и напряжения загруженной ВЛ.


Рис. 2.2.
уравнения [15]:
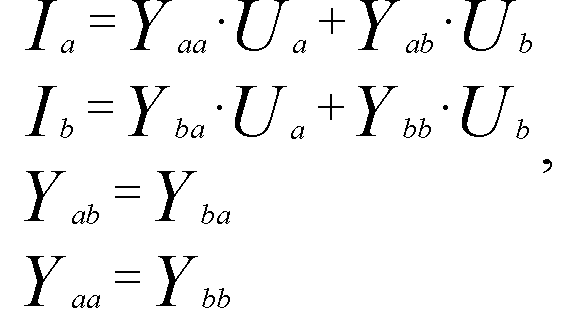
Учет емкостной проводимости позволит уточнить не только величину z, определяемую по формуле (1), но и величину самой емкостной проводимости. Если представить ВЛ в виде П-образной схемы замещения (рис. 2.2), то ей будут соответствовать известные
(2-2)
где Yaa, Ybb, Yab, Yba - собственные и взаимные узловые проводимости ВЛ, соответствующие схеме замещения.
Решение системы уравнений (2.2) позволяет найти узловые проводимости:
![]()
(2-3)
Если учесть, что для схемы рис. 2.2 справедливы соотношения:
![]()
(2-4)
где Ζ и Υ - полные сопротивление и проводимость ВЛ длиной L, то можно найти искомые удельные параметры:

(2-5)
Здесь, как и в формуле (1), токи и напряжения могут быть комплексными величинами, как и искомые величины. Однако, незнание угла между напряжениями и, как следствие, угловая погрешность токов может привести к искажению соотношений между активной и реактивной составляющими «z» и «у» и к появлению активной составляющей в поперечной проводимости «у» соизмеримой с реактивной. В лекции 1 показано, что потери в изоляции ВЛ и на корону дают активную составляющую по крайней мере на порядок меньшую реактивной. Основываясь на этом можно подобрать такой угол между напряжениями, чтобы выполнялось это условие и окончательно определить «у» (точнее составляющую «ό»), например, можно использовать расчетный угол.
Следующий этап уточнения параметров ВЛ связан с представлением ВЛ в распределенных параметрах [15]:
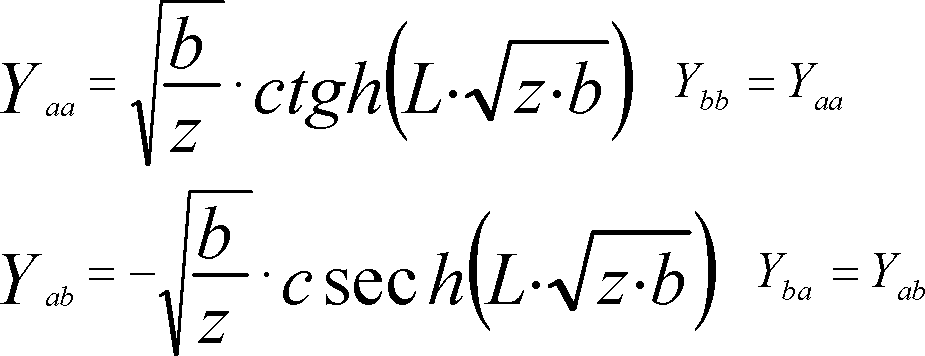
Величины собственных и взаимных проводимостей можно найти из (2.3), однако прямое использование этих уравнений для определения «z» и «b» невозможно, поскольку эти уравнения относятся к категории трансцендентных, допускающих только численное решение одним из известных методов. Однако, в данном случае, любой численный метод должен основываться на вариации удельных параметров таким образом, чтобы они максимально соответствовали зафиксированным токам и напряжениям. Возможно использование готовых математических программ минимизации многомерных функций [16].
Например, в качестве критерия соответствия можно ввести некоторую функцию, минимум которой будет означать, что достигнуто это максимальное соответствие:
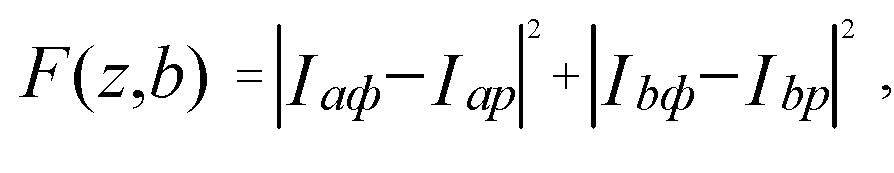
(2-7)
где индекс «ф» обозначает, что токи фиксированные, индекс «р» - расчетные. Алгоритм поиска минимума функции строится следующим образом. Задается приближенное значение удельных параметров ВЛ (например расчетные значения). На их основе находятся значения узловых проводимостей ВЛ (2.6). Затем рассчитываются узловые токи ВЛ с использованием фиксированных напряжений:
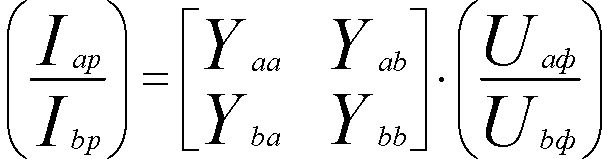
(2-8)
Определяется величина функции. Вносятся изменения в удельные параметры, и весь изложенный расчет повторяется, включая расчеты новых значений узловых проводимостей и новое значение функции. Расчеты повторяются то тех пор, пока не будет найден глобальный минимум функции. Удельные параметры ВЛ, соответствующие этому минимуму можно считать близкими к истинным. Такой алгоритм позволяет эффективно использовать готовые математические программы минимизации многомерных функций [16].
При использовании этого метода предполагается, что в окрестности вариации параметров ζ и Ь, имеется только один минимум функции F.
2. Идентификация параметров ВЛ, связанной взаимоиндукцией с другими ВЛ.

Наличие взаимоиндукции с одной или несколькими параллельно следующими ВЛ заметно усложняет решение поставленной задачи.
Возможно неограниченное количество вариантов параллельного следования ВЛ, по всей длине, участками в различных сочетаниях. Если ВЛ представлены в распределенных параметрах, то нахождение параметров взаимоиндукции еще более усложняется. Известные решения нахождения параметров узловых проводимостей для двух параллельных ВЛ [17], [18] (рис. 2.3), представленных в распределенных параметрах, позволяют создать алгоритм, основанный на минимизации функции аналогичной (2.7), в которой могут быть использованы токи изучаемой ВЛ или всех ВЛ. В основу ложится уравнение:

где Yabcd - матрица узловых проводимостей двух параллельных ВЛ, связанных взаимоиндукцией, вычисленная согласно [18] и являющаяся функцией искомых параметров. Минимизируемая функция выглядит следующим образом:
![]()
(2-10)
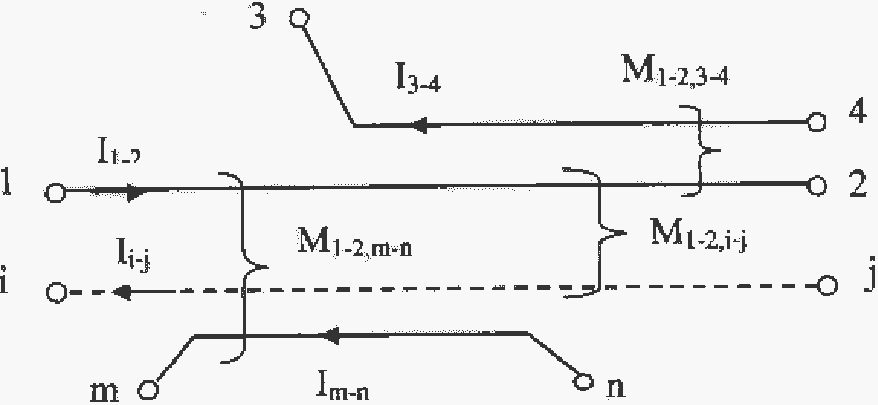
Рис. 2.4.
где суммирование осуществляется по индексу «i», который пробегает индексы расчетных и фактических токов принятых для расчета. Пример использования такого алгоритма дан в приложении 3.
Трудности возникают при формировании алгоритма нахождения параметров изучаемой ВЛ, с которой участками следуют несколько параллельных ВЛ (рис. 2.4).
Упрощенный, но дающий одиночных ВЛ, при этом считается, что величина взаимоиндукции известна.
Во многих случаях величины токов Ii-j не фиксируются, особенно в тех случаях, когда параллельные ВЛ отходят и приходят не на те подстанции, к которым привязана интересующая в данном случае ВЛ. Выход из положения возможен путем использования расчетных величин. Рассчитывается короткое замыкание в том месте, где оно имело место. Находятся расчетные токи короткого замыкания нулевой последовательности интересующей ВЛ и токи ВЛ связанных с ней взаимоиндукцией. Находится отношение фактического и расчетного токов основной ВЛ:
удовлетворительные результаты вариант решения такой задачи, также возможен. Известно соотношение между напряжениями ВЛ и токами параллельных ВЛ через величину взаимоиндукции:
![]() (2.11)
(2.11)
где суммирование идет по индексам i-j. Отсюда следует возможность замены скорректированными напряжениями истинных зафиксированных напряжений:
![]() (2.12)
(2.12)
что эквивалентно исключению влияния взаимоиндукции (рис. 2.5). Используя Uа-b ВМЕСТО Uа-b ДЛЯ определения параметров, можно применять все формулы и методы раздела 1, определенные для
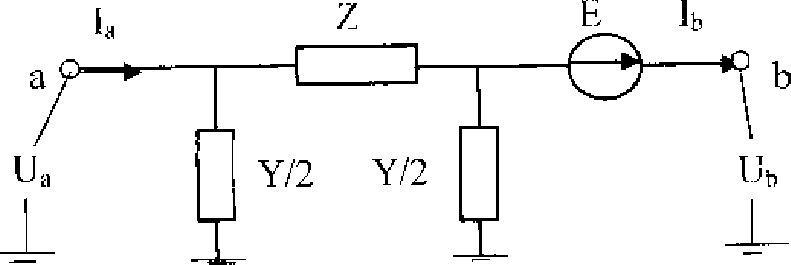
Рис. 2.5.

В формуле (11) производится замена токов:
![]()
(2.13)
(2.14)
и производятся необходимые вычисления. Конечно, такая замена носит приближенный характер, но такой путь все же лучше по сравнению с тем, когда не учитывается влияния токов обусловленный взаимоиндукцией.
ВЫВОДЫ
- Идентификация параметров ВЛ на основе данных регистраторов аварийных событий (коротких замыканий) в энергосистеме является необходимым и возможным мероприятием, позволяющим уточнять расчетные параметры.
- Использование исходных данных, получаемых от регистраторов аварийных событий, позволяет по каждой изучаемой ВЛ накапливать статистические материал, что позволит дополнительно уточнять параметры ВЛ и определять фактическую погрешность.
- Наиболее универсальным способом нахождения параметров ВЛ является итерационный метод последовательного уточнения удельных параметров. Именно такой метод наиболее эффективен при представлении ВЛ в распределенных параметрах с возможным учетом влияния взаимоиндукции и уточнением ее параметров. При этом предпочтительно использование готовых математических программ минимизации многомерных функций.
- Необходимо дальнейшее совершенствование способов и аппаратуры регистрации аварийных событий обеспечивающих фиксацию векторов напряжений по концам ВЛ.

