ЛЕКЦИЯ 1. Основные принципы расчета параметров ВЛ.
Интерес к расчетам параметров ВЛ появился после 1891 года, когда известный ученый и инженер электротехник М.О. Доливо-Добровольский продемонстрировал преимущества трехфазного переменного тока, который и лег в основу развития электроэнергетики [1], [2]. Почти сразу встал вопрос о расчете электрических режимов, в том числе и тех, которые связаны с короткими замыканиями (КЗ). На первом этапе решение таких задач шло довольно сложным путем, в расчетах использовались известные к тому времени такие понятия как индуктивность и емкость и уравнения электромагнитного поля. Упрощение расчетов пришло в 1900 году, когда известный ученый Г. Ми дал строгую теорию распространения гармонического колебания вдоль проводов, в частности он показал, что в этом случае индуктивность и емкость не имеют самостоятельного значения, имеет смысл некоторая функция от них, связанная с частотой переменного тока. Говоря современным языком, он ввел понятия индуктивного и емкостного реактивного сопротивления переменному току:
![]() (1-1)
(1-1)
где ω - угловая частота, f - частота переменного тока, L- индуктивность, С емкость.
Важным шагом в совершенствовании расчетов было введение в 1893 году известным электротехником Ч.П. Штейнмецом комплексных чисел для описания электрических величин переменного тока [3]. Известная в свое время книга Ф. Кессельринга [4] уже включала комплексные числа в расчеты коротких замыканий. Наконец, в 20-ых годах прошлого века был разработан метод симметричных составляющих для расчета симметричных и несимметричных электрических режимов [5], [6], основанный на известной теореме Фортескью о представлении несимметричной системы векторов как суперпозицию симметричных систем векторов. Уже в [4] уделяется большое внимание расчету параметров ВЛ как продольных комплексных сопротивлений, так и емкостных проводимостей. Однако в России инженерный путь расчета начался с выходим в свет книги Н.Н. Щедрина [7]. В современном виде расчеты параметров ВЛ представлены в [8] и [9].
Будем считать, что параметры ВЛ заданы, если известны: удельные продольные сопротивления, активное и индуктивное, удельная поперечная проводимость, активная и емкостная и длина ВЛ. Эти параметры должны быть представлены в виде трех составляющих, а именно: прямой последовательности, обратной и нулевой. Однако первые две равны друг другу, поскольку замена чередования фаз напряжений, поданных на ВЛ и следовательно протекающих токов не связано с изменением каких-либо электромагнитных процессов.
Продольное индуктивное сопротивление прямой (обратной) последовательности определяется по формуле [8], [9]:
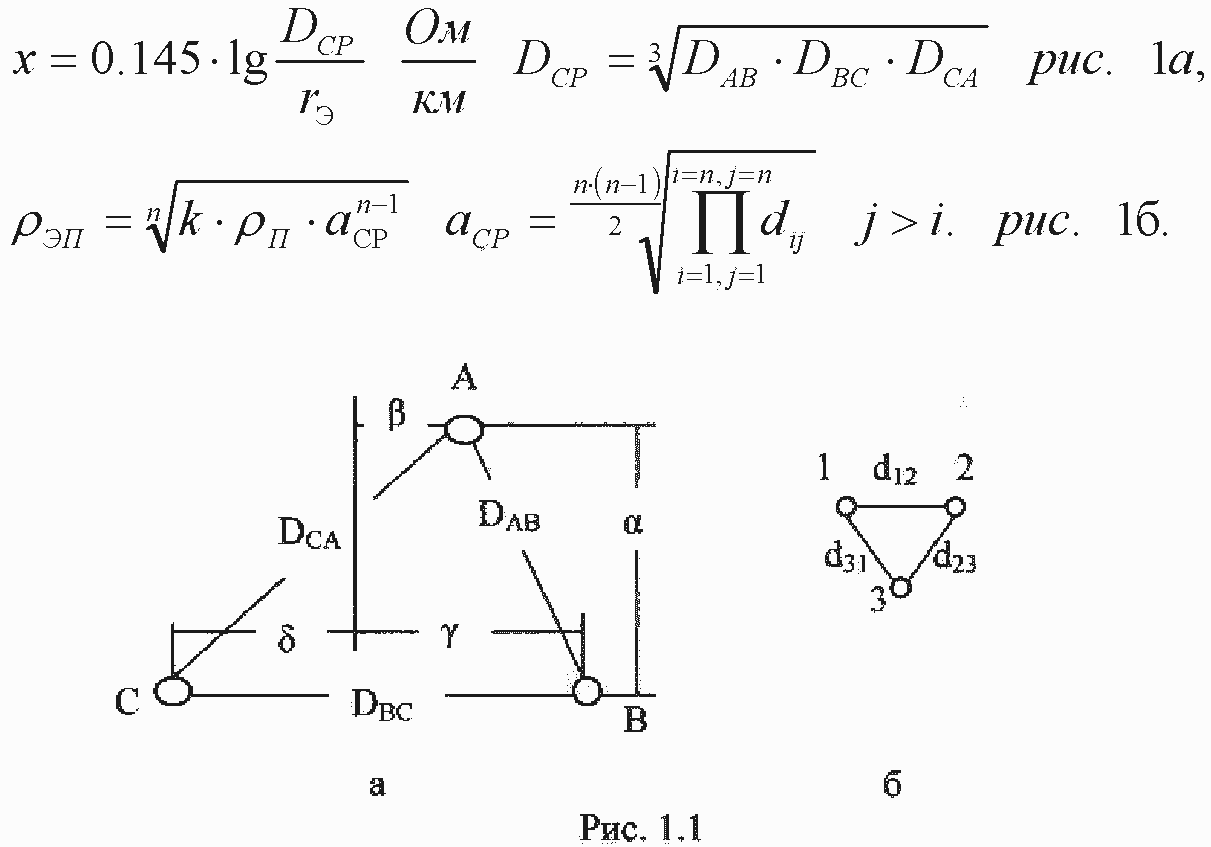
Продольное сопротивление ВЛ, прямая последовательность.
(1-2)
В этих формулах: рп - действительный радиус провода, к - коэффициент учитывающий материал провода, материал стального троса, количество повивов токопроводящей части провода, п- количество проводов в фазе. На практике допустимо применять некоторую среднею величину к = 0,89. Формулы (1.2) будут справедливы для любого количества проводов в фазе, если принять при п = 1 аср = 1. Активная составляющая сопротивления ВЛ зависит от марки провода и количества проводов в фазе. Эти сведения приводятся в справочниках. В результате рождается удельное комплексное сопротивление ВЛ:
![]() (1-3).
(1-3).
Здесь и далее строчные буквы обозначают удельные параметры, прописные - параметры, относящиеся ко всей длине ВЛ.
Оценка погрешности упомянутых расчетных величин возможна, но достаточно сложна. Сама величина Dcp имеет малую погрешность (десятые доли процента), поскольку для данного вида опоры расстояния между проводами известны точно. Другое дело, что каждая ВЛ имеет в своем составе несколько видов опор, а в расчет принимаются расстояния между проводами тех опор, которые составляют большинство. Однако можно предположить, что погрешность за счет не учета различных типов опор даст также небольшую погрешность. При необходимости ВЛ можно представить состоящей из нескольких участков с разными типами опор и тем самым уменьшить погрешности. Провис проводов для этих составляющих также не имеет большого влияния на погрешность. Эквивалентный радиус провода тоже не должен иметь заметной погрешности, поскольку расстояния между проводами фазы жестко закреплены распорками и известны точно. Активная составляющая провода дается в справочниках достаточно точно. Учет влияния температуры воздуха и самого провода для ВЛ 10 кВ и выше скорее важен для расчета потерь, чем для расчета токов короткого замыкания.
Таким образом, для удельных продольных сопротивлений ВЛ можно сделать вывод, их расчетная величина не должна существенно отличаться от фактической и погрешность не должна превысить 2-3 %. Что касается длины ВЛ, то здесь вопрос несколько сложнее. Изменения проектной трассы ВЛ при строительстве и реконструкции не всегда попадает к специалистам по расчетам. Особенно это касается ВЛ 6-110 кВ. Конечно, возможно использование ГИС - технологий для уточнения трасс ВЛ, но это пока удовольствие дорогое и применимо к ВЛ более высоких напряжений. Отсюда вывод, погрешность длины ВЛ может быть основным источником погрешности полных продольных сопротивлений ВЛ.
Поперечная проводимость, прямая последовательность.
Емкостная проводимость определяется по известной формуле:

где Saa, Sbb,SСС - расстояния между проводами и их одноименными зеркальными отражениями в земле (рис. 1. 2а), Sab', Sbc', Sca' - расстояния между проводами и их не одноименными зеркальным отражении- ями в земле (рис.1.2, а). Отсутствие и наличие тросов и их количество практически не влияет на емкостную проводимость прямой (обратной) последовательности. Единственное, что, пожалуй, подлежит уточнению, это величины S, при определении которых следует считаться с провесом проводов. В [9] расчетную высоту провеса провода (рис. 1.2,б) рекомендуется определять по формуле:
![]() где f - стрела провеса. (1-5)
где f - стрела провеса. (1-5)

Взгляд на формулы (1.4) показывает, что в них не видно других источников, которые бы явились источниками большой погрешности. Все величины, входящие в формулы достаточно точно определены. Погрешность длины ВЛ и в этом случае остается одной из основных составляющих результирующей погрешности.
В отличие от реактивной, емкостной составляющей активная составляющая проводимости является величиной слабо определенной. Ее появление обусловлено двумя причинами: утечками активного тока через изоляцию ВЛ и потерями на корону, которые также носят активный характер. Величина потерь, обусловленная первой причиной, составляет небольшую долю от потерь, обусловленных второй причиной, и даже не упоминается литературе [10], [11]. Величина потерь, обусловленных второй причиной, коронным разрядом, не является постоянной величиной. Два основных фактора влияют на величину потерь: погодные условия и величина фактического напряжения. В [10] приводится следующая таблица:
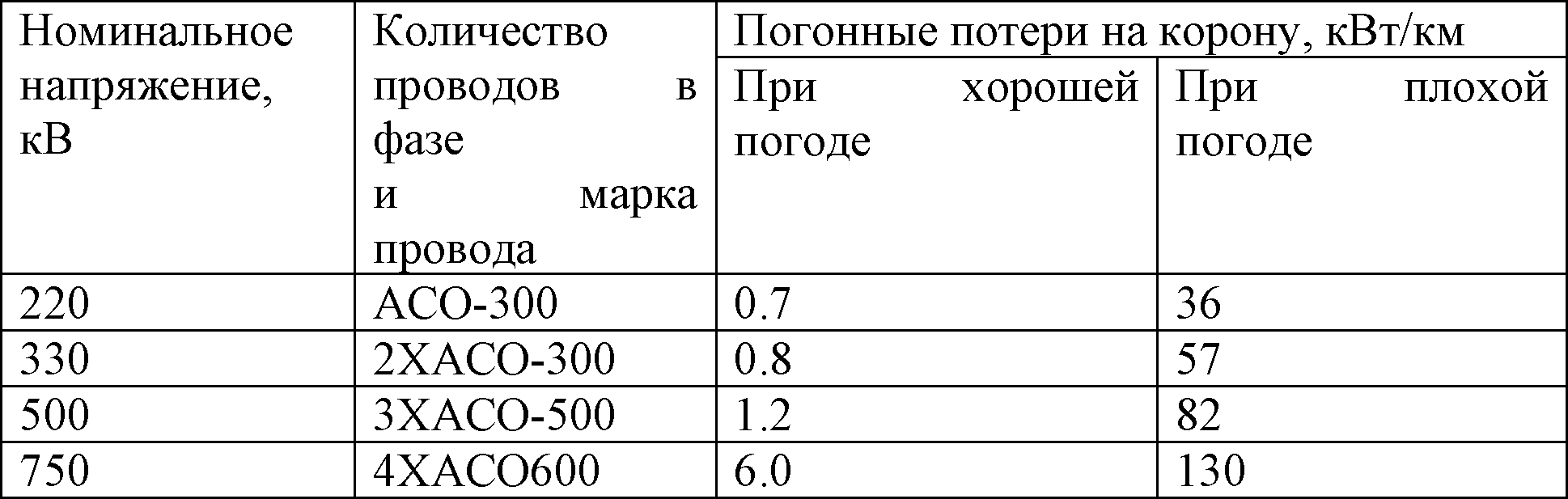
Там же приводится таблица зависимости величины максимальных потерь от фактического напряжения на ВЛ, которая дополнена строкой расчета активной составляющей проводимости:

Активная проводимость вычислялась по формуле:
![]() (1.6)
(1.6)
Нелинейный характер проводимости налицо, что, естественно вносит затруднения в учет этой проводимости. В [10] и [11] приводятся таблицы средних значений емкостной проводимости ВЛ, которые для широкого диапазона напряжений находятся в пределах (2-4)·10-6 Сим/км, что по крайней мере на порядок больше активной составляющей. Из этого следует, что при расчетах токов короткого замыкания активной составляющей проводимости можно пренебречь, ввод ее в схему необходим при расчете потерь в ВЛ. Погрешность длины ВЛ при расчете полной проводимости ВЛ также, как и при расчете продольных сопротивлений, будет одной из основных составляющих результирующей погрешности. В целом можно сказать, что погрешность параметров ВЛ прямой (обратной) последовательности не превысит 2-3 %. Если учитывать обе составляющие, то комплексная проводимость будет выглядеть следующим образом:
![]() (1.6)
(1.6)
Продольное сопротивление ВЛ, нулевая последовательность.
Сопротивление нулевой последовательности ВЛ состоит, как и сопротивление прямой (обратной) последовательности, из двух составляющих: активной и реактивной (индуктивной).
Индуктивное сопротивление для одноцепной ВЛ без троса определяется по формуле:
![]() (1-7)
(1-7)
где Dз- глубина возврата обратного тока в земле, Рср - средний геометрический радиус трех проводов ВЛ:
![]() (1-8)
(1-8)
под корнем величины из (1.2).
Сразу возникает вопрос о величине Dз. Рекомендуемая величина 1 000 м справедлива для грунтов с хорошей проводимостью. Однако грунты многолетнемерзлые, скалистые и некоторые другие требуют уточнения этой величины. Некоторые исследования говорят о том, что глубина возврата обратного тока может достигать 8000 и даже 10000 м. Другими словами возникает неопределенность и, как следствие, погрешность, которую можно оценить. Рассмотрим отношение реактивных сопротивлений нулевой последовательности при крайних значениях глубины обратного тока. Исходные данные для расчета приведены в таблице:

Расположение проводов взято из рис. 1.1. Вычисление величин Dпроизводилось по формулам: ![]()
Результаты расчета сведены в следующую таблицу:

Удельное индуктивное сопротивление прямой последовательности принято: х1(110 кВ)=0.4 Ом/км, х1(330 кВ)=0.321 Ом/км. Результаты расчета показывают, что отличие сопротивлений нулевой последовательности, вычисленных для различных глубин возврата обратного тока, могут достигать 30 - 37 %. Известны поправки к формулам расчета индуктивной составляющей, учитывающие наличие и количество грозозащитных тросов [9]. Однако, от этого суть дела не меняется. Это означает, что фактическая величина сопротивлений нулевой последовательности требует уточнений путем проведения искусственных или естественных экспериментов.
Активное сопротивление ВЛ нулевой последовательности состоит из двух составляющих: активного сопротивления провода и активного сопротивления земли. Последнее, как отмечено в [8], [9], почти не зависит от проводимости земли и вычисляется по формуле:
![]() (1.9)
(1.9)
Комплексное удельное сопротивление нулевой последовательности предстанет в виде:
![]() (1-10)
(1-10)
где rпр - сопротивление провода, rзем - сопротивление земли.
Поперечная проводимость, нулевая последовательность.
Величина этой поперечной проводимости зависит от нескольких факторов, таких как габариты самой ВЛ, наличие и количество тросов. Основная формула расчета поперечной проводимости выглядит следующим образом:

Все расстояния берутся согласно рис. 1.2.
Наличие троса увеличивает емкостную проводимость, два троса также увеличивают емкостную проводимость. Это увеличение учитывается соответствующими формулами [9]. Из анализа формулы (1.11) можно сделать вывод, что, если верна теория, то, особо большой погрешности в определении емкостной поперечной проводимости не ожидается.
Взаимоиндукция, индуктивная составляющая.
Взаимоиндукция является одним из самых плохо определенных параметров. Действительно, удельная величина взаимоиндукции зависит прежде всего от взаимного расположения трасс параллельно следующих ВЛ. Трассы таких ВЛ носят самый разнообразный характер. ВЛ могут идти на одинаковом расстоянии по всей длине трассы или только на некоторых участках, ВЛ могут сближаться или расходиться. Кроме того, взаимоиндукция зависит от глубины возврата тока в земле. В расчетах взаимоиндукция представляется сопротивлением взаимоиндукции, которое состоит из активной и реактивной части. Удельное сопротивление взаимоиндукции для двух параллельно следующих ВЛ без тросов определяется по формуле:

![]()
Схема расположения проводов показана на рис. 1.3. В случае наличия п параллельно следующих ВЛ и т тросов индуктивная составляющая сопротивления взаимоиндукции определяется по более сложной формуле [9], однако ее использование необязательно, если общее явление взаимоиндукции системы ВЛ представить попарно. Из формулы (1.12) следует зависимость величины сопротивления взаимоиндукции от глубины возврата обратного тока в земле, что вносит дополнительную неопределенность в расчетную величину и, следовательно, погрешность.
Взаимоиндукция, активная составляющая.
Активная оставляющая обусловлена тем. что к электродвижущей силе, которая наводится вдоль ВЛ благодаря явлению взаимоиндукции, добавляется падение напряжения на сопротивлении земли, рис. 1.4. В [8] показано, что величина этого сопротивления мало зависит от проводимости земли,
определяется по формуле (1.9) и носит постоянный характер.
В результате между каждой парой проводов, связанных взаимоиндукцией, образуется сопротивление взаимоиндукции:
![]()
Из двух составляющих формулы (113) большую погрешность имеет вторая, мнимая составляющая.
Из изложенного материала следует, что экспериментальное определение параметров ВЛ необходимо, особенно это касается параметров связанных с составляющими нулевой последовательности.

Рис. 1.4.

