Традиционно для определения искажения синусоидальности кривой напряжения в трехпроводных сетях используются модели, в которых нелинейные нагрузки задаются источниками токов высших гармоник [52, 86, 88]. В схемах замещения сети для частот высших гармоник элементы сети задаются полными сопротивлениями, рассчитанными для данной частоты. Падение напряжения на эквивалентном полном сопротивлении сети от тока определенной гармоники, величина которого известна заранее, дает значение напряжения данной гармоники. Рассчитав необходимое количество схем замещения (по числу учитываемых гармоник), определяют коэффициент искажения синусоидальности кривой напряжения сети.
Очевидно, что подобные модели имеют ряд недостатков. Во- первых, они не позволяют исследовать электромагнитные процессы в сети с нелинейной нагрузкой вследствие формального характера построения схем замещения. Во-вторых, значение токов высших гармоник определено, очевидно, при условии питания нелинейной нагрузки от сети бесконечной мощности и без учета влияния параметров конкретной сети. В-третьих, параметры схем замещения элементов сети для частот высших гармоник в настоящее время определяются по-разному с существенными расхождениями в результатах у разных авторов.
Все эти недостатки особенно остро проявляются при моделировании сетей НН с нелинейными нагрузками. Характерные особенности сетей НН, а именно, наличие нулевого провода и относительно низкие значения мощностей короткого замыкания, оказывают существенное влияние на протекание электромагнитных процессов. Это, в свою очередь, приводит к значительному изменению значений высших гармоник тока в конкретной сети НН по сравнению с посчитанными при условии питания нелинейной нагрузки от сети бесконечной мощности. Поэтому модели, в которых нелинейные нагрузки задаются источниками токов высших гармоник, непосредственно, если их не адаптировать, нельзя использовать в сетях НН. В связи с этим, существует потребность в создании математических моделей для исследования электромагнитных процессов в сетях НН с нелинейными нагрузками в целях определения их влияния на сеть с учетом конкретных параметров сети и нагрузки.
Следует отметить, что в настоящее время известны работы, посвященные анализу процессов на входе нелинейных электроприемников, в частности, выпрямителей с учетом параметров их входной цепи. Например, в (10] рассмотрены искажения синусоидальности кривых напряжений в СЭС ЭВМ с трехфазными ИВЭП с бестрансформаторным входом. При этом получены аналитические зависимости коэффициента искажения синусоидальности кривой напряжения от угла коммутации, который, в свою очередь, меняется при изменении нагрузки, параметров генераторов и мощности короткого замыкания. В работе [100] выполнено моделирование системы «питающий кабель — неуправляемый однофазный выпрямитель, нагруженный на RС-цепь» с помощью программного пакета OrCAD 9.2 и получены зависимости интегральных характеристик этой системы, в частности, искажений синусоидальности кривых входных тока и напряжения от параметров системы. В работе [77] приведены результаты анализа процессов в локальной распределительной сети, к которой подключена выпрямительная нагрузка. При этом рассматривается упрошенная однофазная схема замещения сети, которая формируется на выходе агрегата бесперебойного питания. Таким образом, в упомянутых работах при моделировании рассматриваются лишь отдельные элементы сети НН, которые не отражают особенностей ее построения, что, в результате, не позволяет адекватно оценить влияние нелинейных электроприемников на сеть.
При разработке математической модели сети НН с нелинейной нагрузкой необходимо учитывать следующие обстоятельства.
С одной стороны, она должна обеспечивать моделирование электромагнитных процессов с необходимой точностью и не быть при этом чрезмерно сложной. С другой стороны, при относительной простоте модели в схемах замещения должно быть представлено достаточное количество элементов сети и нагрузки в целях определения их влияния на величину высших гармоник.
Как известно, в сетях НН получили широкое распространение импульсные источники электропитания электронной техники. В качестве входного звена таких источников питания используется сетевой выпрямитель, обычно неуправляемый, параметры которого наряду с параметрами низкочастотного емкостного фильтра в наибольшей степени определяют характер и форму потребляемого тока. Сетевой выпрямитель может быть однофазным или трехфазным, причем однофазные выпрямители более характерны для сетей НН. Результаты анализа режимов работы однофазных сетевых выпрямителей с емкостным фильтром [33] показывают, что потребляемый из сети ток имеет импульсный характер, форма которого зависит не только от параметров емкостного фильтра, но и от параметров питающей сети, т.е. однофазный выпрямитель с емкостным фильтром является характерной нелинейной нагрузкой низковольтных сетей. При этом его макромодель при относительной простоте позволяет проводить анализ электромагнитных процессов с учетом параметров выпрямителя и питающей сети. В связи с этим представляется возможным в модели сети НН рассмотреть в качестве нелинейного элемента нагрузки однофазный выпрямитель, нагруженный на RС-цепь (рис. 2.5).
В реальных условиях эксплуатации средства электронной техники подключаются к конкретной сети НН. Как было отмечено выше, параметры сети оказывают влияние на значения токов и напряжений нагрузки. Поэтому для определения истинного влияния нелинейной нагрузки на сеть питания необходимо моделировать не только нагрузку, но и сеть, к которой она будет подключена. С учетом отмеченных выше требований можно построить математическую модель сети НН с нелинейной нагрузкой на основе двух известных: модели трехфазной четырехпроводной сети с линейной нагрузкой и модели нелинейной нагрузки. При этом основными допущениями будут следующие: подведенные напряжения образуют симметричную и неизменную систему прямой последовательности, все элементы сети за исключением нагрузки линейны и симметричны, диоды выпрямителей идеальны.
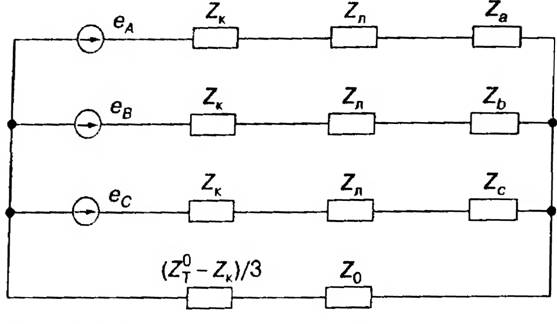
Рис. 2.6. Схема замещения сети НН
С учетом особенностей построения сети НН (сеть выполняется трехфазной с нулевым проводом, а большинство потребителей — однофазные), ее схема замещения имеет вид, показанный на рис. 2.6 [167]. Здесь еА, ев, ес— трехфазная симметричная система ЭДС; Ζκ, Ζτ — сопротивления короткого замыкания и нулевой последовательности трансформатора; Ζ0, ΖΛ — сопротивления нулевого и фазного проводов линии; , Zc — три произвольных нагрузочных сопротивления, параллельно которым подключаются упомянутые нелинейные элементы нагрузки.
Разработанная модель трехфазной четырехпроводной сети с выпрямительной нагрузкой позволяет провести расчет всех токов и напряжений конкретной сети НН [48]. Данная модель учитывает параметры сетей НН, а именно мощность и схему соединения обмоток трансформатора, исполнение, длину и сечение линии, коэффициент мощности, а также параметры выпрямительной нагрузки. В результате в схеме замещения элементы сети и нагрузки представляются соответствующими сопротивлениями, причем расчет проводится на основной частоте. Значения токов и напряжений данной сети определяются одновременно решением дифференциальных уравнений, описывающих линейные схемы, формируемые по этапам проводимости ключевых элементов (диодов) однофазных выпрямителей.
Полученные значения токов и напряжений используются для определения соответствующих коэффициентов рядов Фурье, с помощью которых рассчитываются коэффициенты п -х гармонических составляющих тока (напряжения) синусоидальности кривой
тока и коэффициенты искажения синусоидальности кривой напряжения
и коэффициенты искажения синусоидальности кривой напряжения
и(n) — действующие значения составляющих основной частоты и п-х гармонических составляющих токов и напряжений соответственно).
Результаты проведенных расчетов для конкретных вариантов исполнения сети НН позволяют анализировать влияние выпрямительной нагрузки на форму кривых токов и напряжений. Пусть мощность трансформатора 10/0,4 кВ, 25 кВ А; схема соединения обмоток звезда—звезда с нулем; cos φ = 0,8; линия выполнена кабелем 3x25 + 1x10 мм2; на фазные напряжения сети НН подключены три одинаковые нагрузки, одна из которых показана на рис. 2.5. При этом параметры однофазной нагрузки остались такими, как в предыдущем параграфе. В результате расчета получаем измененные по сравнению с вариантом питания от сети бесконечной мощности значения коэффициентов искажения синусоидальности кривых тока. Величина гармоник тока выпрямителя сильно уменьшилась, при этом Квып = 56,78 %. Форма тока в линейной части нагрузки несколько отличается от синусоидальной. В сети ограниченной мощности сказывается влияние выпрямительной нагрузки. В результате суммарный фазный ток сети НН будет существенно отличаться от теоретического, рассчитанного для сети бесконечной мощности. Его коэффициент искажения синусоидальности кривой Кк = 13,57 %. Наконец, получено конкретное значение несинусоидальности фазного напряжения. Коэффициент искажения синусоидальности кривой напряжения в данном случае равен 18,66 %.
Очевидно, что при изменении варианта исполнения сети (другие схема соединения обмоток трансформатора, исполнение линии 0,4 кВ, cos φ, а и т.д.) изменится и значение несинусоидальности токов и напряжений [139]. Рассмотрим, как влияет доля выпрямительной нагрузки а на форму кривой напряжения. Проведенные расчеты подтверждают тот факт, что значение а в значительной мере определяет несинусоидальность фазного напряжения сети. На рис. 2.7 даны зависимости коэффициентов искажения синусоидальности кривой Ки и n-й гармонической составляющей К напряжения от значения а.

Рис. 2.7. Зависимости коэффициентов искажения синусоидальности кривой Ku и n-й гармонической составляющей Кu напряжения от значения доли выпрямительной нагрузки
Очевидно, что с увеличением доли выпрямительной нагрузки возрастает несинусоидальность напряжения. Причем кривые, описывающие изменения Ки и Кт, имеют характер степенной функции. Остальные зависимости К носят сложный характер при общей тенденции возрастания с ростом а.
Нетрудно видеть, что искажение формы кривой напряжения определяется в основном напряжением третьей гармоники. Остальные гармоники вносят незначительный вклад. Причем напряжения гармоник нулевой последовательности (кроме третьей) сравнимы по значению с напряжениями гармоник прямой и обратной последовательностей, хотя, как показывают расчеты, токи гармоник, кратных трем (кроме третьей), невелики. Доминирующее влияние напряжений гармоник, кратных трем, можно объяснить большим эквивалентным сопротивлением нулевой последовательности сетей с нулевым проводом.
В продолжение анализа влияния изменения варианта исполнения сети НН в работе [41] проведено сравнение результатов расчета высших гармоник сети при использовании трансформаторов со схемой соединения обмоток звезда—зигзаг с нулем и звезда—звезда с нулем. Как известно, основным недостатком трансформаторов со схемой соединения обмоток звезда—звезда с нулем является относительно большое Ζ, которое определяется
конструктивными особенностями трансформатора, схемой соединения его обмоток, степенью насыщения стержней магнито- провода и др. Такая особенность указанных трансформаторов делает их чувствительными к несинусоидальности фазных токов в сетях НН с нелинейными нагрузками. В результате проведенных расчетов было определено, что по сравнению с трансформатором, обмотки которого соединены по схеме звезда—звезда с нулем, использование трансформатора с соединением обмоток по схеме звезда—зигзаг с нулем приводит, в частности, к снижению Кu на 20—50 % (в зависимости от доли и параметров выпрямительной нагрузки) при некотором ухудшении гармонического состава фазного тока.
В работе [39] рассмотрено влияние параметров нагрузочных режимов трансформатора на несинусоидальность токов и напряжений в сети НН. В результате проведенного анализа было установлено, что известное технико-экономическое требование о том, что во всех случаях необходимо стремиться к наиболее полному использованию номинальной мощности трансформатора и даже целесообразно работать в режиме систематической перегрузки, в случае нелинейных нагрузок получает дополнительную аргументацию. Снижение коэффициента загрузки трансформатора в упомянутом случае, с одной стороны, не приводит к существенному снижению уровня высших гармоник, а с другой — может привести к временным перенапряжениям в сетях НН.
Очевидно, что рассмотренная математическая модель низковольтной сети с выпрямительной нагрузкой позволяет определить искажение синусоидальности кривых токов и напряжений сетей НН с сосредоточенной в одном узле нагрузкой. Это могут быть либо неразветвленные автономные сети с нагрузкой, имеющей в своем составе радиоэлектронную аппаратуру с ИВЭП с бестрансформаторным входом, либо распределительные (городские или сельские) сети НН, питающие нагрузку крупных объектов (зданий, предприятий), которая имеет в своем составе нелинейные электроприемники.
Если предположить, что данная нагрузка является, например, эквивалентной нагрузкой всех электроприемников жилого или общественного здания, то тогда полученное искажение синусоидальности кривой напряжения на нагрузке будет соответствовать несинусоидальности фазного напряжения на вводе в здание, а искажения синусоидальности кривой тока в линии — несинусоидальности фазного тока внешней питающей сети. В действительности каждый электроприемник сети НН подключается в какой-то конкретной точке к внутренней сети здания и имеет ток и напряжение, форма кривых которых отличается от формы кривой фазного тока внешней питающей сети и напряжения на вводе в здание, соответственно. Очевидно, что рассмотренная модель не позволяет определить значения высших гармоник токов и напряжений внутренней сети электроснабжения здания и, соответственно, искажения синусоидальности их кривых на зажимах подключенных к ней электроприемников, а полученные значения несинусоидальности токов и напряжений из-за погрешности эквивалентирования всей нагрузки сети в одном узле могут быть неточными. Кроме того, при проведении сравнительного анализа режимов рассматриваемой сети НН в различных вариантах ее исполнения такие параметры, как доля нелинейной нагрузки или коэффициент загрузки трансформатора, определяются формально, без конкретизации состава и графиков нагрузок отдельных групп электроприемников. В связи с этим данную модель следует рассматривать как упрощенную, и актуальна задача ее усовершенствования путем дополнительного учета конкретных параметров всех основных элементов электрической сети здания.

