ОБРАБОТКА ЦИФРОВЫХ ОСЦИЛЛОГРАММ ДЛЯ АВТОМАТИЗИРОВАННОГО АНАЛИЗА
Цифровые осциллографы, как правило, хранят информацию в следующем формате (рис. 5.6): а(0), б(0), с(0), д(1), б(1), с(1),...
В этой последовательности в скобках указаны дискретные времена.

Рис. 5.6. Иллюстрация движения “окна наблюдения”, переводящего осциллограммы в последовательность комплексных чисел
Для наглядного представления эту запись можно представить в форме матрицы:
![]()
(5 1)
где в каждой строке приведены данные по всем каналам для соответствующего момента времени, а в каждом столбце — данные по соответствующему каналу, упорядоченные по времени.
Как было указано выше, для объектов с 220 кВ достаточно определить действующее значение величин а,б, с и их фазу. Действующее значение Ак (рис. 5.6) наиболее просто определить по выражению:
![]()
(5.2)
Под “окном наблюдения” в этом случае понимается 12 точек (число отсчетов на период на рис. 5.6), начиная с точки к = 0. Далее, для получения следующего действующего значения можно сдвигать “окно наблюдения” из точки к = 1 последовательно до точки к = 12. Совершенно очевидно, что вычисления со сдвигом на период будут выполняться для всей осциллограммы в 12 раз быстрее, но результат даст более грубую оценку. Так как вопрос о шаге движения “окна наблюдения” должен решаться для конкретных случаев, то программа автоматической обработки осциллограмм позволяет задать этот шаг персоналу любым. Целесообразно первоначально использовать настройку с шагом, равным периоду.
Определение фазы сигналов, при отсутствии апериодической составляющей, можно производить по переходам через нуль. Чтобы избежать операции извлечения корня подсчитывают A1, а значения, которые должны сравниваться с этой величиной (уставкой) возводят в квадрат.
Еще одним способом вычисления является ортогональное разложение. Если рассмотреть синусоидальный сигнал
![]()
и этот же сигнал, сдвинутый на 7/4
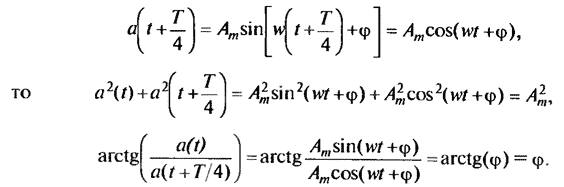
(5.3)
При обработке осциллограмм получить сдвиг на Т/4достаточно легко. Так в примере на рис. 5.6, достаточно взять точки с номерами, сдвинутыми на три единицы (число отсчетов на период 12 и, следовательно, 12/4 = 3). Следует отметить, что расчеты по (5.2) дают действующее значение синусоидальной величины, а по (5.5) — амплитудное. Это не имеет существенного значения для синусоидального сигнала, так как действующее и амплитудное значения связаны постоянным коэффициентом
![]() (5.7)
(5.7)
Для несинусоидального сигнала это соотношение не выполняется. Очевидно, оба способа не дают погрешности для синусоидального сигнала. Если сигнал несинусоидальный (например, содержит апериодическую составляющую), то будут возникать погрешности Для преодоления трудностей с обработкой несинусоидальных сигналов используется цифровая фильтрация (которая существенно замедляет обработку) или контроль за стабильностью значений, что эквивалентно ожиданию затухания переходного процесса.
Для моделирования функционирования измерительных органов могут требоваться действующие, средние или амплитудные значения и фаза сигнала. По этой причине часто вычисляются сразу все значения. Если в примере рис. 5.6 передвигать “окно наблюдения” с шагом, равным периоду, то при двенадцати отсчетах на период (каждый отсчет 2 байта) объем осциллограммы, байт, составит п * 12-2, где п — число записанных периодов.
После обработки каждый период будет представлен действующим, средним, амплитудным значением и фазой. Все эти числа имеют размерность не менее 4 байт, т.е. п * 16. Таким образом, обработанная осциллограмма на одну треть меньше исходной по объему. Если “окно наблюдения” двигать на (1/12) Г, то объем осциллограммы, байт, составит п * 12 * 16, т.е. в 8 раз больше исходной.
5.4. ВОЗМОЖНЫЕ МЕТОДЫ АНАЛИЗА ФУНКЦИОНИРОВАНИЯ РЗА
Для анализа функционирования РЗА по данным регистрации дискретных и аналоговых сигналов может быть использован следующий подход По аналоговым величинам определяется, какие измерительные органы должны были сработать. Для каждого набора сигналов измерительных органов заранее определяются возможные последовательности для регистрируемых сигналов. Эти последовательности сравниваются с последовательностью, полученной при регистрации. При таком подходе общее число последовательностей может оказаться очень большим. Если рассмотреть вместо последовательностей число функций, которые могут образовывать последовательности, то общее число функций только для двух регистрируемых сигналов составит 24 = 16 (см. приложение 2).
При рассмотрении именно последовательностей двух сигналов, которые переключаются из положения единицы в ноль (или из нуля в единицу), т.е. при ситуации срабатывание — возврат, общее число переключений будет четыре. Для четырех переключений число перестановок будет 4! = 24.
Статический анализ предлагается использовать для диагностики устройств РЗА [5]. Обоснованием такого подхода для автоматической диагностики может служить то обстоятельство, что число возможных функций хотя и большое, но конечное. Кроме того, при автоматической диагностике каждая функция отражает либо исправность УРЗА, либо какую-то неисправность или неисправности, следовательно, каждая из них должна иметь определенный комментарий. Так как в задаче анализа функционирования УРЗА основным фактором является время получения решения, а точная диагностика не требуется, желательно использовать другой подход.
Анализ последовательностей, полученных от задачи регистрации, можно выполнить значительно быстрее, если перебирать не все последовательности (как отмечалось, диагностика в темпе аварийного процесса не требуется), а сравнивать зарегистрированную последовательность с эталонной. В этом случае возможно получить решение типа правильно (неправильно) функционировало УРЗА. В качестве эталонной последовательности может выступать результат работы модели УРЗА при сигналах на ее входе от ЦО или иного источника аналоговых сигналов. Достоинством такого подхода является возможность получения эталонных последовательностей для достаточно сложных аварий (наложение событий, переходы одного вида КЗ в другое и т.д.). Этот подход и получил распространение для решения анализа функционирования УРЗА [4, 9, 10].
