Об уточнении места повреждения на ВЛ с изолирующими распорками в расщепленных фазах

Дунаев А. И.

Определение места повреждения (ОМП) в [1] рассмотрено с точки зрения традиционной техники РЗ. При использовании для ОМП формул, полученных после замены N-проводной ВЛ соответствующим числом параллельных симметричных трехпроводных цепей, неизбежны, как минимум, погрешности от неучета несимметрии исходной ВЛ относительно точки повреждения. При использовании табличного метода ОМП отмечена необходимость поиска места повреждения в трех точках ВЛ.
Эти недостатки ОМП могут быть устранены, если использовать модель несимметричной N-проводной ВЛ и методы решения систем нелинейных уравнений.
Для более ясной демонстрации различий сравниваемых подходов к ОМП будем считать, что на линии не применялась транспозиция проводов. Для большей наглядности изложения материала и легкости повторения результатов рассмотрим однородную шестипроводную ВЛ, а для ограничения объема - только повреждение в одной точке на фазе А.

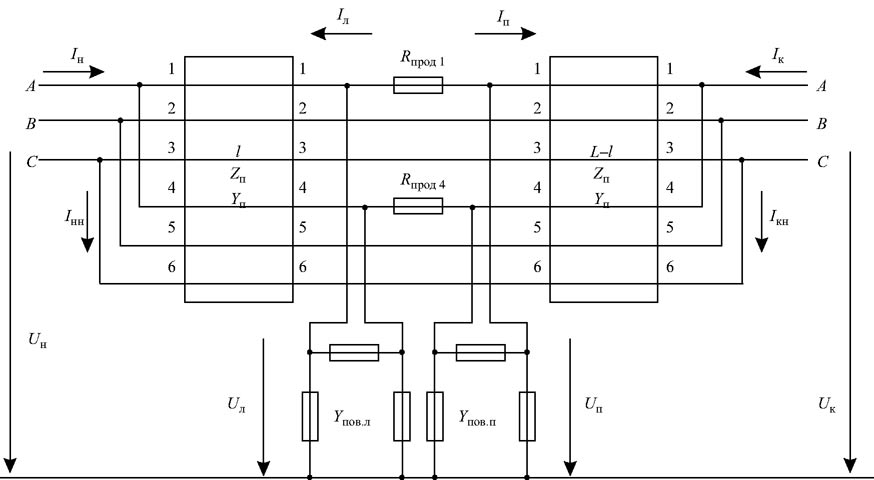
Схема замещения ВЛ при повреждении фазы A:
UH, IH - напряжение и ток в начале линии; ик, 1к - напряжение и ток в конце линии; IHH, 1кн - неизвестный ток в начале и конце ВЛ; иё, ип - напряжение с левой и правой сторон повреждения; !л, !п - ток с левой и правой сторон повреждения; 7повл, Упов п - треугольник поперечной аварийной несимметрии с левой и правой сторон повреждения

При принятых условиях модель (схема замещения) ВЛ полностью определяется данными о длине ВЛ L и матрицах размера (6 х 6) погонных продольных сопротивлений ZH и погонных поперечных проводимостей Yu. Повреждение на фазе A в первом приближении можно определить данными о месте повреждения l и о значении двух треугольников поперечной аварийной несимметрии (Упои.л и Гпов.п) с обеих сторон двух сопротивлений продольной несимметрии (Rпрод1, Rпрод4). Схема замещения ВЛ, соответствующая описанным условиям, изображена на рисунке. Для компактности изложения стороны ВЛ обозначены индексами “н” и “к”, а токи и напряжения - в форме массивов- столбцов. Положение векторов тока или напряжения любого провода ВЛ в каком-либо столбце определяется соответствующим номером провода (цифры от 1 до 6).
Пусть известны векторы напряжений (UH и ик) и векторы только суммарных токов проводов (IH и Ik) каждой фазы, измерения на каждой стороне ВЛ выполняются в независимых системах координат (базисах) и векторы напряжений, например, фазы В, совмещаются с осью действительных чисел.
Если требуется определить только место повреждения, то неизвестными величинами будут: расстояние до места повреждения с начала ВЛ l; угол взаимного поворота базисов (УВП); шесть векторов тока проводов (IHH и Ikh).
Для их определения необходимо составить 14 независимых скалярных или 7 векторных (комплексных) уравнений.
Первый случай. Есть подозрение на обрыв одного или обоих проводов фазы A. Необходимым условием этого случая будут неуспешное АПВ и увеличенное затухание высокочастотного тракта по фазе A на отключенной ВЛ. Достаточным условием может быть результат локационного способа ОМП, так как для его применения на отключенной ВЛ создаются идеальные условия. Для отстройки от скачков напряжений в местах обрывов в систему уравнений не включаются граничные условия для напряжений фазы A. При этом можно составить несколько систем уравнений, например, такую:

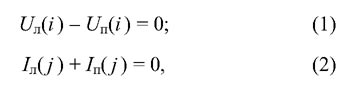
где i = 2, 3, 5, 6 и j = 2, 3, 5 - номера проводов.
Параметры режима ВЛ в уравнениях (1) и (2) определяются из следующих матричных выражений: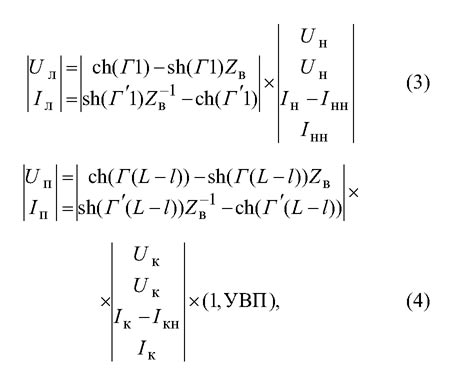
где Г, Г' и Z% (волновое) - матрицы (6 х 6) вторичных параметров несимметричной шестипроводной ВЛ (в фазных координатах), которые являются
функциями от матриц ZH и Уп; (1, УВП) = (модуль, аргумент) - комплексное число в полярной форме.
Более детальные сведения о функциях от матриц и о телеграфных уравнениях N-проводной ВЛ можно найти, например, в [2].
Данные о параметрах предаварийного нагрузочного режима не обязательны, но их наличие позволяет использовать данный метод для аварийных составляющих параметров режима повреждения и расширяет возможности моделирования режима при анализе работы данного метода ОМП.
Второй случай. Обрывы проводов фазы A отсутствуют. Достаточным условием этого случая будет неизменность затухания высокочастотного тракта по фазе A ВЛ после самоустранения или отключения повреждения. Семь векторных уравнений (1) и (2) системы можно составить по линейным критериям. Например, пять уравнений можно составить по линейным напряжениям, а два - по линейным токам неповрежденных фаз в виде:
/л(2) + /д(2) - /л(3) - 1п(3) = 0.                      (5)
Критерии по линейным величинам позволяют максимально отстраиваться от влияния параллельных ВЛ, нестабильностей эквивалентной глубины возврата тока в земле и стрел провеса проводов и от падений напряжения на заземляющих устройствах подстанций с обеих сторон ВЛ.
В обоих рассмотренных случаях методы ОМП являются модификациями метода типа ДФР [3]. При использовании вариантов методов ОМП типов ДФН или ДФИ [3] переменная УВП получается известной и система уравнений содержит 13 скалярных уравнений.
Для случая девятипроводной ВЛ меняется только число уравнений и число возможных комбинаций повреждений. Каждый пункт транспозиции или каждая сосредоточенная поперечная несимметрия с известными сопротивлениями (шунтирующие реакторы, трансформаторные отпайки и др.) только увеличивает на единицу число однородных участков ВЛ. Вопросы о виде повреждения и переходных сопротивлениях в месте КЗ в данном случае считаются самостоятельными задачами и могут решаться после определения места повреждения. При отлаженной системе ОМП значительное различие результатов расчета по первому и второму случаям может служить косвенным признаком обрыва провода.
Принципы численного решения систем нелинейных уравнений были заложены задолго до появления линий электропередачи. Но принципа общего аналитического решения этих систем в математике не существует до сих пор. С появлением вычислительной техники развитие численных методов решения систем нелинейных уравнений часто шло по пути последовательного использования нескольких способов, различных для разных классов задач. Это определяется тем, что чем совершеннее и быстрее способ, тем меньше обычно диапазон для выбора начальных значений (НЗ) неизвестных величин.
Известно, что метод перебора в принципе позволяет найти все решения системы с заданной точностью, но его непродуманное применение может загрузить любой компьютер вычислениями на несколько лет. Однако иногда грамотное использование этого метода может позволить найти решение быстрее и достовернее, чем при применении других способов оптимизации (минимизации) функций многих переменных.
Более оптимистичные заявления автора противоречили бы утверждениям специалистов-матема- тиков о том, что в численных методах существует довольно много “ловушек”, а для решения ряда задач необходима “не только вычислительная мощность процессора, но и интеллект специалиста”.
Детальную информацию о методах решения систем нелинейных уравнений можно найти в большинстве учебников по численным методам.
Результаты вычислительных экспериментов для первого случая при l = 300 км. ВЛ моделировалась с использованием телеграфных уравнений как одиночная линия длиной 396,8 км при двустороннем питании. Каждая из систем моделировалась симметричной системой векторов фазных ЭДС с модулем 400 кВ и сопротивлениями в форме (R; X) в омах
Z1 = (1; 20); Z2 = (1; 18); Z„ = (4; 22).
Активные сопротивления недиагональных комплексов матрицы погонных продольных сопротивлений задавались равными 0,05 Ом/км, а диагональных - 0,067 Ом/км. Реактивные сопротивления в той же матрице, записанные по строкам верхнетреугольной формы, равны (в омах на 1 км)

Активная составляющая погонной поперечной проводимости принималась по традиции равной нулю. Емкостные составляющие комплексов матрицы Уп, записанной по строкам верхнетреугольной формы, равны (в сименсах на 1 км) |Bn| = \7,1326; - 0,20268; - 0,057902; - 5,10;

1. 0,14602; - 0,049473; 7,1879; - 0,1965; - 0,28412;
2. 5, 0627; - 0,14602; 7,1631; - 0,069462; - 0,28412;
3. 5,1003; 7,1631; - 0,19650; - 0,057902; 7,1879;
4. 0,20268; 7,1326| • 10 -6.

Начальные значения (НЗ) тока в проводах 5, 6 неповрежденных фаз принимались равными половине соответствующего суммарного тока. Начальные значения (НЗ) тока в проводе 4 принимались равными нулю или суммарному току фазы A, чем имитировались случаи обрывов различных проводов указанной фазы.
При отсутствии погрешностей в задании параметров ВЛ и отсутствии инструментальных погрешностей измерения токов и напряжений решение системы сходилось к 300 км с заданной точностью во всех рассмотренных далее случаях. Поэтому далее приводятся результаты экспериментов при условии, что ток фазы A в начале ВЛ измерен с погрешностью -2%.
Для решения системы использовался метод одновременного решения уравнений (Ньютона - Якоби). Время решения системы на среднепроизводительном IBM РС составляло около 10 с.
Первый пример повреждения рассматривался для трех нагрузочных режимов: прием активной мощности, работа ВЛ без перетока активной мощности и выдача активной мощности. Последующие примеры повреждений рассматриваются только для режима работы ВЛ без перетока активной мощности. Результаты каждого примера приводятся в следующей форме:
(расчетный угол [эл.град.] УВП): НЗ [эл.град.] для УВП/НЗ [км] для l - результат ОМП [км] в предположении обрыва провода № 1//НЗ и результат ОМП в предположении обрыва провода № 4.

1. Обрыв провода 1, КЗ провода 1 на землю слева от обрыва через 10 Ом и справа - через 25 Ом:
1. (19):              24/250 - 306,6097//24/350 - 306,6095;
2. (- 1,7): - 3/390 - 302,628//- 3/200 - 302,629;
3. (- 22): - 27/270 - 297,739//- 27/330 - 297,744.
2. КЗ провода 1 на землю через 25 Ом без обрыва провода:

(-1,1): - 3/350 - 299,649//- 3/350 - 299,650.

1. КЗ провода 1 на землю через 25 Ом и КЗ между проводами 1 и 4 через 0,01 Ом без обрыва провода:

(-1,1): - 3/350 - 293,979//- 3/350 - 294,024.

1. Обрыв провода 1 и КЗ слева от обрыва, как в примере 3:

(- 1,1): - 3/350 - 293,979//- 3/350 - 294,024.

1. Обрыв провода 1, КЗ слева от обрыва, как в примере 3, и КЗ на землю справа от обрыва через 25 Ом:

(- 1,3): - 3/250 - 301,165//- 3/250 - 301,178. Более детальный анализ представляется логичным при проведении его самим потенциальным пользователем рассмотренных программных продуктов.

Выводы

1. Неоднозначность определения места повреждения в рассмотренных случаях отсутствует.
2. Погрешности описанных методов ОМП при допущении о том, что ВЛ является линейной кусочно-однородной цепью с постоянными параметрами схемы замещения ВЛ и источников мощности, определяются только инструментальными погрешностями исходных данных: параметров модели и параметров режима ВЛ.
3. При прочих равных условиях способы ОМП по составляющим промышленной частоты, использующие менее детальную модель ВЛ или математически менее строгую постановку задачи ОМП, чем рассмотренные, будут давать более точный результат только в тех редких случаях, когда сумма всех их методических и инструментальных погрешностей будет стремиться к нулю.
4. Рассмотренные методы ОМП абсолютно повторимы, но требуют соответствующей специализации и творческой инициативы. Предприятие “Электросетьсервис” может оказывать консалтинговые услуги по внедрению указанных методов ОМП в практику сетевых предприятий.

Список литературы

1. Особенности ОМП на ВЛ с изолирующими распорками в расщепленных фазах / Мисриханов М. Ш., Попов В. А., Якимчук Н. Н., Медов Р. В. - Электрические станции, 2001, № 1.
2. Микуцкий Г В. Каналы высокочастотной связи для релейной защиты и автоматики. М.: Энергия, 1977.
3. Дунаев А. И. О новой технологии ОМП на ВЛ. - Энергетик, 2001, № 2.