- Расчет одиночных свай на горизонтальные и комбинированные нагрузки
Расчет на горизонтальную нагрузку методами теории упругости ввиду трехмерности задачи значительно сложнее, чем расчет на вертикальную нагрузку. Но, главное, при горизонтальном нагружении нелинейные деформации в массиве грунта и возникшие в нем зоны предельного состояния не локализуются на поверхности сваи уже при очень малых нагрузках. Поэтому, строго говоря, расчет методами теории упругости в принципе невозможен, а его использование в качестве некоторого приближения требует различных допущений. В дальнейшем речь будет идти, как правило, только о расчете по методу коэффициента отпора.
Обоснование применимости этого метода в случае горизонтальной нагрузки принципиально не отличается от приведенного выше для случая вертикальной нагрузки. Можно даже добавить, что большая степень развития пластических явлений должна, по-видимому, способствовать большей локализованности взаимодействия, т. е. большей адекватности контактной модели коэффициента отпора.

Рис. 11. Схема расчета свай на податливых опорах:
а - принципиальная схема; б - характер деформации оси сваи и изменения сопротивления грунта по глубине; в - кривая горизонтального сопротивления грунта р, и на i-м уровне
Таким образом, для расчета свай на поперечные и комбинированные нагрузки принимается обобщенная винклеровская модель основания, характеризуемая переменным по глубине нелинейным коэффициентом горизонтального отпора или горизонтальной сопротивляемости. При использовании численных методов расчета, таких, как МКР и МКЭ, эта контактная модель становится элементом дискретной расчетной схемы, которая представляет собой балку, опирающуюся на достаточно большое число податливых опор (рис. 11). Закономерности перемещений опор можно регулировать и изменять в широких пределах, моделируя тем самым деформируемость реального грунтового основания. Дискретная расчетная схема позволяет программировать все изменения в закономерностях перемещений, отражать различные критические события и состояния. При этом можно по-разному задавать работу каждой из податливых опор в зависимости от конкретных условий работы сваи и свойств грунтов.
Вывод определяющих уравнений проведем для комбинированного продольно-поперечного нагружения. Поскольку будем рассматривать только активное нагружение без разгрузки, реакцию основания можно представить как реакцию нелинейно-упругого тела, у которого, как известно, деформирование сопровождается накоплением потенциальной энергии:
![]() (3)
(3)
где и — горизонтальные перемещения точек оси сваи на глубине z; w — то же, вертикальные; Ul — энергия сопротивления острию сваи.
Принимается гипотеза, что все силы и перемещения лежат в плоскости χ0z, причем ось z совпадает с осью сваи и направлена вниз, начало координат 0 находится на поверхности грунта. Для линейно-упругой контактной модели винклеровского типа
![]() (4)
(4)
Для более общей модели
![]()
При помощи конкретной формы выражения U(u, w) можно учесть не только нелинейность реакции грунта, но и взаимовлияние продольной и поперечной реакций. Например, горизонтальное перемещение вызывает обжатие грунта и может увеличить как начальный коэффициент продольной реакции, так и предельное трение. С другой стороны, то же поперечное смещение может за счет локального разрушения (разупрочнения) грунта снизить вертикальный отпор. Очевидно также, что изгиб ствола сваи приводит к перераспределению продольных и поперечных усилий. Вопрос о взаимодействии продольной и поперечной реакции грунта изучен пока очень слабо и поэтому затрагиваться в дальнейшем не будет.
Будем рассматривать сваю как идеально линейно-упругий стержень, работающий на сжатие (EF) и изгиб (EJ), тогда потенциальная энергия системы "свая—грунт" записывается в виде

кривизна изогнутой оси.
Здесь величины со штрихами обозначают соответственно первое и второе дифференцирование по z. Сразу выделять в этих формулах главные члены нельзя, поскольку при дальнейших преобразованиях члены более высокого порядка малости могут оказаться важными.
Из общих теорем теории сплошных сред следует, что решению соответствует минимум потенциальной энергии системы, а минимум интегрального функционала, как известно из вариационного исчисления, достигается на кривых, удовлетворяющих уравнениям Эйлера—Лагранжа. В данном случае получаем уравнения равновесия в виде

Выражения (6) и (7) — это условия равновесия элемента сваи в проекциях на оси z и х соответственно. Можно выразить эти условия через действующие в поперечном сечении силы и момент, а также реакции отпора.
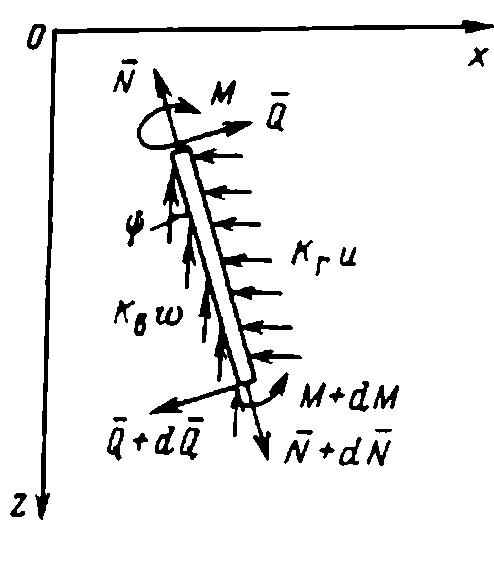
Составим уравнения равновесия сваи (рис. 12), имеющего до деформации длину dz, а после ds=(1+ϵ)dzp:
Рис. 12. Силы, действующие на элемент сваи


либо даже не учитывалось влияние продольной силы на изгиб, т. е. продольные и поперечные перемещения и усилия считались независимыми (подобный подход к расчету горизонтально нагруженных свай использован в СНиП П-17-77).
Из системы уравнений следует, что даже при чисто горизонтальном нагружении возникает продольная сила и соответствующее ей перемещение свай. Действительно, допустим противное, т. е. что перемещения w равны 0. Тогда из (29) следует, что в теле сваи возникают растягивающие усилия. Эти усилия должны вызывать продольные перемещения точек ствола сваи, которые частично компенсируют растяжение, пока не наступает равновесие. Опыты, проведенные в МИСИ с моделями свай диаметром 60 мм и длиной 4 м, показали, что при циклическом чисто горизонтальном нагружении головы сваи наблюдается подъем (около 15 см за 100 циклов) головы сваи, т. е. ее выдергивание из грунта. Объясняется это тем, что при увеличении горизонтальной нагрузки в результате искривления возникают растягивающие усилия (как описано выше), которые вытягивают сваю вверх, а при снятии горизонтальной нагрузки она уже не может вернуться вниз, поскольку этому препятствует затекание водонасыщенного грунта под острие при его подъеме и другие необратимые эффекты.
Выбор вертикального коэффициента отпора Кв рассмотрен в § 5. Горизонтальный коэффициент отпора Кг также удобно представить в виде (2), заменив q на р, a w на и. Вопросу выбора параметров нелинейной зависимости посвящено много работ, детальные рекомендации по этому вопросу приведены в § 9, 10. Здесь изложим кратко только самые общие соображения.
Начальный коэффициент отпора часто принимают изменяющимся по глубине по треугольной эпюре. Частично это отражает ослабление жесткости основания вблизи свободной поверхности, частично — возрастание модуля деформации грунта с глубиной, а частично и нулевое предельное сопротивление у поверхности. Но последний фактор учитывается в нелинейном коэффициенте отпора отдельно, и поэтому можно брать в верхней части основания начальный коэффициент горизонтальной сопротивляемости изменяющимся по трапециевидной эпюре с конечной ординатой на поверхности.
Предельное сопротивление на отдельных участках сваи при ее горизонтальном нагружении определяется различными физическими явлениями. В верхней части сваи определяющую роль играет выпор грунта, а в нижней части — прорезание его сваей. Точка раздела находится из условия равенства сопротивления выпору и прорезанию.
О коэффициенте т в формуле (2) можно повторить то же, что и для случая продольного сопротивления (§ 5): т увеличивается с ростом плотности и связности грунта и изменяется в пределах от 1 до 3.
В общих чертах остановимся на учете в расчете различных факторов, влияющих на напряженно-деформируемое состояние системы "свая- грунт", таких, например, как многократность нагружения. Подавляющее большинство авторов сходится на том, что циклическое нагружение приводит к снижению сопротивляемости грунта. Более того, в результате колебаний свай в верхней их части может возникнуть зона отрыва от грунта, где продольное сопротивление падает до нуля, а поперечное появляется лишь при достаточно больших смещениях [13]. Такое поведение, очевидно, характерно для достаточно прочных грунтов. В наших опытах для рыхлых водонасыщенных песков получена противоположная картина: в процессе циклического нагружения затекание грунта в зоны отрыва приводит к уплотнению и упрочнению околосвайного грунта и увеличению его реакции. Таким образом, влияние многократности нагружения на перераспределение и значение коэффициентов горизонтальной сопротивляемости (которые следовало бы использовать в расчете) нуждается в дальнейшем изучении.
Сваи гидротехнических сооружений часто забиваются под небольшим углом к вертикали. Как показали исследования, малый угол наклона
практически не сказывается на работе сваи на продольную нагрузку Несколько иначе обстоит дело с поперечной нагрузкой. Очевидно, что в этом случае предельное сопротивление грунта выпору в разных направлениях будет различным. Однако в крутонаклонных сваях, забитых под углом к вертикали не более 8—10°, это можно не учитывать.
При определении расчетных параметров кривых нелинейного деформирования следует обращать внимание на особенности работы песчаного грунта в водонасыщенном состоянии. Немногочисленные экспериментальные данные свидетельствуют о значительном увеличении деформативности сооружений, взаимодействующих с таким основанием, однако в нормативной литературе это не нашло отражения.
Остановимся на вопросе о выборе граничных условий при реализации расчетной схемы.
Граничные условия на острие сваи формируются при помощи коэффициентов отпора, связывающих лобовое сопротивление (продольное усилие в конце ствола), изгибающий момент и поперечную силу при z=l соответственно с продольным перемещением острия, его поворотом и поперечным перемещением. Обычно моментом и поперечной силой на конце пренебрегают, но при использовании численных методов в этом нет необходимости. Коэффициенты отпора можно принять нелинейно зависящими от перемещений.
Граничные условия в голове сваи выбираются с учетом жесткости ее заделки в конструкцию сооружения. При наличии свободной длины сваи между заделкой и поверхностью грунта можно поступить двумя способами:
а) включить свободный участок в расчетную длину сваи, приняв коэффициенты отпора нулевыми и граничные условия в голове сваи;
б) граничные условия с головы сваи перенести на поверхность грунта на основе решения задачи о продольно-поперечном иpгибе-сжатии свободного участка сваи.
Первый способ нам представляется более простым.

