Расчет свайных оснований ГTC - Расчетные параметры свай в несвязных грунтах

• Расчетные параметры свай в несвязных грунтах

При теоретической интерпретации результатов экспериментов выявлена необходимость проведения расчетов свай любой категории жесткости при различных законах изменения к по глубине и различных способах закрепления их голов. Для этого использовался метод конечных разностей, основная идея которого состоит в замене дифференциального уравнения изгиба сваи его конечно-разностным приближением и алгебраическом решении системы уравнений, полученных для нескольких точек по длине сваи. При этом граничные условия (силовые и геометрические) на концах свай принимались в соответствии с конкретной схемой опыта. Закон изменения коэффициента горизонтальной сопротивляемости грунта по глубине задавался в виде массива коэффициентов к для большого числа расчетных сечений по длине сваи (например, п = 20). Подстановкой  в программу (алгоритм вычислений реализован на ЭВМ) экспериментально установленных законов изменения к была дополнительно проверена правильность подсчета реактивного давления по рекомендуемой выше методике, что контролировалось опытными значениями деформаций стволов свай и изгибающих моментов.
Для оценки различных предложений выбора закона изменения коэффициента сопротивляемости по глубине, в том числе и рекомендуемого СНиП II-17-77 линейного закона, произведены сравнения измеренных и расчетных эпюр u(z), M(z) и σ(z). На рис. 20 и 21 приведены сопоставления графиков, построенных исходя из линейного закона k(z) = k1Mz/l (k1M - коэффициент к на глубине z=1 м) для различных этапов нагружения. Значение коэффициента выбиралось из условия соответствия какой-нибудь критериальной экспериментальной величине, в данном случае смещению головы свай u0.
Расчеты показали, что линейный закон дает хорошее соответствие лишь при малых относительных перемещениях u0/d ≈ 0,04—0,05 на уровне поверхности грунта. В случае свай средней жесткости (В) и гибких (Г) при развитии значительных перемещений u0/d>0,2-0,3 значения изгибающего момента оказались заниженными на 10—25 % и более. Степень развития пластических деформаций и закон изменения коэффициента сопротивляемости зависит от перемещения и характера изгиба сваи. Следовательно, любой экспериментально установленный закон k(z) может соответствовать только какому-то одному моменту в нагружении сваи; с развитием пластических деформаций значения к уменьшаются, что наглядно иллюстрируется опытами (рис. 22).

Рис. 20. Линейные эпюры изменения коэффициента к по глубине (а) и рассчитанные по ним эпюры горизонтальных деформаций сваи u(z) (б), изгибающих моментов M(z) (в) и реактивного давления грунта σ(z) (г) для сваи типа А при различных ступенях нагрузки H0:
1 - 4,2 кН; 2 - 6,3 кН; 3 - 8,7 кН; 4-11 кН; о - экспериментальные точки

Рис. 21. Линейные эпюры изменения коэффициента к по глубине (а) и рассчитанные по ним эпюры горизонтальных деформаций сваи u(z) (б), изгибающих моментов M(z) (в), реактивного давления грунта σ(z) (г) для свай типа Г при различных ступенях нагрузок H0:
2-10 кН; 2 - 20 кН; 5-30 кН; 4 - 35 кН; о - экспериментальные точки


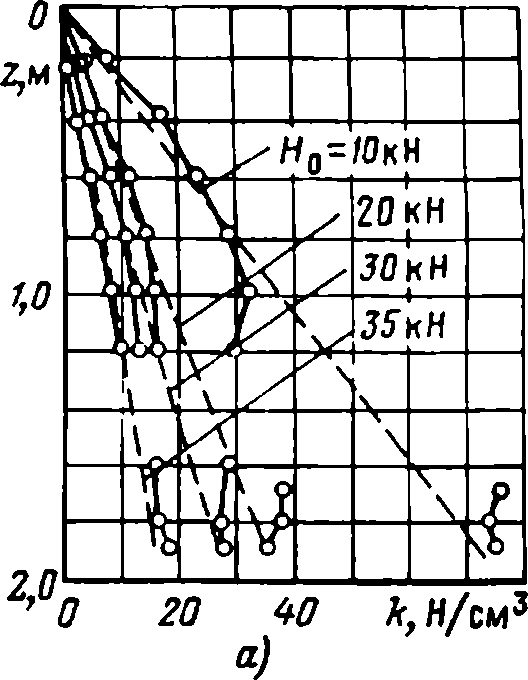
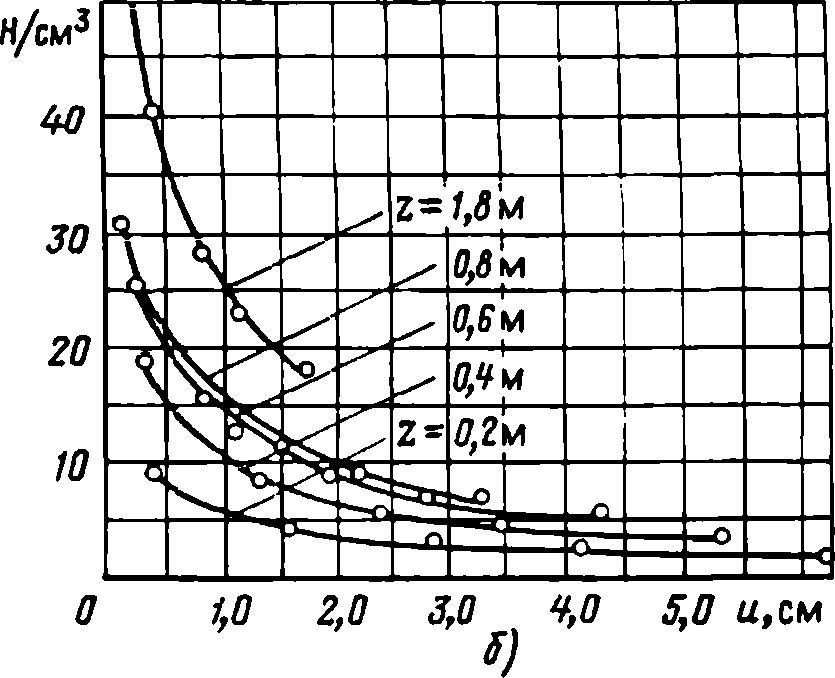
Рис. 22. Графики изменения коэффициента к с ростом нагрузки H0, по результатам опытов со сваей типа А (а), и с ростом перемещений и, для различных сечений по глубине z(б), С - экспериментальные точки
Сопоставительные расчеты показали также, что для гибких (длинных) свай, погруженных в однородный грунт, решающее значение имеет правильность назначения коэффициента сопротивляемости в наиболее активной части сваи — верхней (примерно 1/3l, где l - глубина погружения), а далее его значение можно считать постоянным.

Рис. 23. Графики нелинейного деформирования σ(u), аппроксимированные зависимостью (36) по результатам испытаний свай типов А (○) и Б (●) в песках средней плотности (а) и для сваи типа А в песках рыхлого сложения (б) для различных глубин z

Из рис. 20 и 22 следует, что в случае жестких (коротких) свай треугольная форма эпюры изменения коэффициента сопротивляемости в  зависимости от глубины хорошо соответствует экспериментальным данным для различных этапов горизонтального нагружения. Это не противоречит сделанным ранее выводам о нелинейности изменения к с глубиной, поскольку объясняется, во-первых, схемой работы сваи и, во-вторых, тем, что изгибающие моменты в бесконечно жестких сваях не зависят от значения к [11].
Таким образом, на основании приведенных результатов, можно сделать вывод, что важнейшая расчетная характеристика — коэффициент горизонтальной сопротивляемости грунта к, широко используемый в практических расчетах горизонтально нагруженных свай, является сложной функцией глубины, перемещений, характера изменения механических свойств основания и изгибной жесткости сваи, размеров поперечного сечения и т. п., для которой получить аналитическое выражение в замкнутой форме не представляется возможным.
Экспериментально установлено, что эпюра коэффициента сопротивляемости по глубине при малых нагрузках для свай различной жесткости имеет линейный характер, что следует иметь в виду при проведении "упругих" расчетов (u0/d < 0,05-0,1).
Из анализа экспериментальных зависимостей между реактивными давлениями и перемещениями (рис. 23) следует, что формы графиков "реакция грунта—перемещения" качественно близки и могут быть выражены одинаковыми функциями кривых с различными параметрами.
Опытами установлено следующее: а) графики σ, и имеют явно выраженный нелинейный характер, особенно в поверхностной зоне грунтового массива; б) эти зависимости на всех глубинах имеют вид кривых, обращенных выпуклостью к оси реактивных давлений, что соответствует уменьшению коэффициента горизонтальной сопротивляемости грунта с ростом перемещений; в) графики деформирования имеют вид кривых, асимптотически приближающихся к некоторому предельному значению давления σпр, которое возрастает с глубиной; г) при увеличении поперечного размера (диаметра) сваи значения реактивных давлении уменьшаются; д) изменение деформативных и прочностных характеристик грунта по глубине выражается в изменении параметров единого криволинейного графика σ, и, в частности в нарастании угла наклона начального участка кривой и в росте предельного давления; е) начальный угол наклона k0 графика σ, и или начальный коэффициент сопротивляемости, обратно пропорционален поперечному размеру сваи (см. ниже); ж) тип закрепления верхнего (нижнего) конца сваи не влияет (во всяком случае, до относительных перемещений u0/d, равных 0,2—0,3) на форму и параметры кривых σ, и.
Наряду с общими требованиями к уравнениям кривых, выражающих нелинейные процессы, т. е. наибольшее приближение к действительным закономерностям, аналитические зависимости для расчетов должны отвечать следующим условиям. Во-первых, начальные участки кривых σ, и (при малых загружениях) должны достаточно точно описывать упругую часть деформаций, что находит отражение в производных функций при(см. рис. 11,в). Во-вторых, график деформирования должен либо асимптотически приближаться к горизонтали при заданном значении σпр, либо быть близким к такому приближению (см. рис. 11,в).
Таким образом, при выборе аналитических функций для кривых принимались во внимание наилучшее соответствие результатам экспериментов, наиболее простой вид зависимости и удобство расчета на ЭВМ.
Этим требованиям, как показали результаты многочисленных крупномасштабных исследований свай в несвязных грунтах, отвечает зависимость вида
(36)
где k0(z) — начальный (касательный) коэффициент горизонтальной сопротивляемости грунта, соответствующий упругому деформированию основания;— предельное значение реактивного давления, достигаемое при значительных перемещениях; u(z) — перемещение сваи в точке с координатой z.
Преимуществом зависимости (36) является то, что одной кривой описывается как допредельное, так и предельное состояние грунта, причем она включает как деформационные (к0), так и прочностные (σпр) его характеристики. Предельное горизонтальное давление на грунт вместе с начальным коэффициентом сопротивляемости являются основными входными параметрами для получения кривых σ, и.
Результаты опытов показывают, что коэффициент горизонтальной сопротивляемости грунта к уменьшается с увеличением поперечного размера сваи.

Учитывая значения коэффициентов постели, представленные в табл. 2, а также результаты наших исследований свай в различных грунтах основания [14, 15, 17, 18], можно в качестве ориентировочных значений градиента начального коэффициента горизонтального отпора К для большинства расчетных случаев рекомендовать данные, приведенные в табл. 3.
Для получения уточненных значений коэффициентов следует проводить исследования грунтов полевыми методами и испытания свай.

Таблица 2

Таблица 3

Изучение работы свай при больших перемещениях показало, что с увеличением горизонтальной нагрузки грунт в верхнем слое приходит в предельное состояние с образованием тела выпирания. В более глубоких зонах основания грунт уже не перемещается к поверхности, а прорезается стволом сваи. Ниже этой зоны основание находится в фазе уплотнения (характерно для длинных свай). Эти выводы хорошо согласуются с результатами экспериментальных исследований, выполненных в нашей стране [3, 6, 17] и за рубежом [46, 50, 57], которыми установлено, что сопротивление грунта перед сваей под действием горизонтальных сил отличается от рассчитанного по традиционной схеме с учетом пассивного давления грунта.

Рис. 24. Схемы поверхностного разрушения основания перед горизонтально нагруженной сваей

В результате проведенных исследований предельного давления на грунт можно отметить, что все существующие решения имеют, как правило, полуэмпирический характер и основаны на том, что в поверхностной зоне разрушение грунта моделируется при помощи трехмерного клина- призмы (рис. 24,а) или "тела выпирания" (рис. 24,б), а ниже критической глубины zκρ разрушение происходит по горизонтальным плоскостям в условиях пластического течения [3, 6, 45, 50, 57].
Опыты, выполненные рядом авторов (Н. В. Лалетин, А. С. Строганов, И. Т. Сергеев, Г. И. Глушков и др.), а также наши исследования показали, что форма "тела выпирания" имеет достаточно постоянный вид: в плане оно имеет форму эллипса или круга, а с боковых сторон ограничивается криволинейной поверхностью. Для приближенного определения предельного горизонтального отпора грунта в зоне выпорав соответствии с результатами исследований было принято, что "тело выпирания" в каждом своем сечении имеет форму, состоящую из прямоугольника шириной d и двух полукругов, а образующая "тела выпирания" в плоскости симметрии наклонена к вертикали под углом Θ (рис. 24,б). Опуская теоретические выкладки, приведенные в [6], запишем окончательное выражение для вычисления:

Рис. 25. Схема разрушения массива грунта перед сваей на большой глубине (а) и расчетная схема для определения сопротивления грунта на этой глубине (б)
где A0, B0, C0 — коэффициенты несущей способности, являющиеся функциями угла внутреннего трения φ; λа — коэффициент бокового давления в активном состоянии предельного равновесия сыпучего тела.
Значения коэффициентов А0, В0, С0 для некоторых углов внутреннего трения φ приведены в табл. 5.
Сравнение опытных данных рпр с расчетными показывает, что лучшее совпадение с экспериментальными данными дает расчет предельного горизонтального давления на грунт в зоне прорезанияпо (38). Для зоны выпора наблюдается некоторый разброс между расчетными и опытными данными. На основании анализа результатов испытаний в песках различной плотности сложения с крупномасштабными моделями, с учетом работ [2, 50, 57] получен эмпирический поправочный коэффициент n0, зависящий от относительной глубины z/d, который необходимо использовать при применении (37) и (38):

Рис. 27. Сопоставление опытных () и расчетных (о) данных для сваи типа В (табл. 1) со свободной (2) и защемленной (2) головой
деформативно-прочностные характеристики основания подобраны правильно, а физическая модель грунта, положенная в основу рекомендуемой методики расчета, хорошо отражает действительную работу системы "свая—грунт".