Глава третья
РАСЧЕТ СОВМЕСТНОГО ВЫБЕГА ТУРБОГЕНЕРАТОРОВ С ЭЛЕКТРОДВИГАТЕЛЯМИ МЕХАНИЗМОВ
СОБСТВЕННЫХ НУЖД
§ 15. Математическое моделирование элементов выбегающей системы
Под механическим выбегом турбогенератора с механизмами с. н. понимают продолжение выработки электроэнергии с постепенно понижающимися частотой и напряжением при отсутствии связи с энергосистемой после закрытия стопорного клапана турбины и прекращения работы отсеченного объема пара. Выработка электроэнергии происходит за счет кинетической энергии вращающихся масс турбогенератора.
Необходимым условием успешного протекания совместного выбега является сохранение устойчивости асинхронных электродвигателей при снижении частоты и уменьшении напряжения. Для выполнения этого условия автоматические регуляторы возбуждения турбогенераторов АЭС оборудуют специальным блоком выбега, поддерживающим напряжение пропорциональным частоте вращения
. Это дает значительный запас устойчивости асинхронной нагрузки, что следует из сравнения максимального электромагнитного момента двигателя с моментом сопротивления механизма вентиляторного типа. При опрокидывании двигателя
= Мс и после подстановки соответствующих выражений получим 
, откуда критическое напряжение
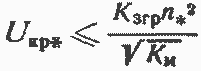
(79)
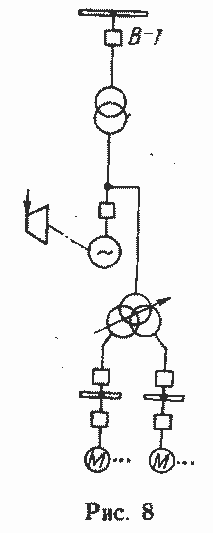
Учитывая оборудование турбогенераторов блоками выбега, а также использование ГЦН с большой инерцией маховых масс, в качестве расчетной может быть принята схема рис. 8.
При сохранении устойчивости выбегающей нагрузки математическое описание процессов при совместном выбеге существенно упрощается. Скольжения и частоты вращения роторов агрегатов с. н. в о. е. можно считать равными скольжению и частоте турбогенератора, поэтому нет необходимости в интегрировании уравнений (1). Мощность, потребляемую выбегающими электродвигателями, можно считать равной мощности приводимого насосного агрегата. Поскольку в совместном выбеге с турбогенератором участвует только часть нагрузки с. и., допустимо пренебречь падением напряжения в трансформаторе с. н. и считать равными напряжения на выводах двигателей и турбогенератора [5]. При этом характер изменения скольжения выбегающей системы описывается одним дифференциальным уравнением движения ротора турбогенератора
где s — скольжение ротора турбогенератора относительно синхронной оси; Ртурб — мощность турбины в процессе выбега; Рп — мощность потерь выбегающей системы, включая и мощность, потребляемую от генератора совместно выбегающими с ним электродвигателями; Tj — инерционная постоянная выбегающей системы;
— избыточный момент выбегающей системы.
Упрощенная методика расчета выбега основана на решении уравнения (80) методом последовательных интервалов с шагом
(81)
где
— изменение частоты вращения выбегающей системы на i-м интервале, в пределах которого ее избыточный момент можно считать неизменным.
Поскольку дифференциальные уравнения (1) исключены из рассмотрения, величины инерционных постоянных агрегатов с. н. необходимо включить в величину Tj выбегающей системы.
При исходном генераторном режиме мощность турбины определяется с учетом запаздывания в закрытии стопорного клапана по сравнению с моментом отключения выключателя и с учетом расширения отсеченного объема пара. Учитывая, что при отказе системы регулирования турбины закон изменения расхода пара до срабатывания стопорного клапана может быть самым различным, важно воспроизвести крутизну переднего фронта нарастания частоты вращения и ее максимальное значение. Это выполняется при использовании следующих упрощенных выражений:
При наличии в составе выбегающей нагрузки насосов, работающих на противодавление, прекращение их подачи происходит при частоте вращения nкл, соответствующей закрытию обратного клапана, несмотря на наличие большого запаса энергии в выбегающей системе. Для преодоления этого недостатка электроснабжение подобных механизмов, а также иных электроприемников, требующих стабильного напряжения по частоте и модулю, можно осуществить через статический преобразователь частоты, представляющий из себя автономный инвертор, питающийся от выпрямленного напряжения выбегающего генератора.
Зная частоту вращения выбегающей системы и практически, равные ей частоты вращения электродвигателей, можно определить подачу насосных агрегатов и таким образом связать процессы в электрической части с технологическими параметрами. Для аппроксимации зависимости подачи от частоты вращения можно предложить следующие упрощенные зависимости:
для механизмов без противодавления
для механизмов, работающих на противодавление, 
где р3 — показатель степени, зависящий от противодавления и уставки открытия обратного клапана насоса nкл. При питании от выбегающего генератора насосов, работающих на противодавление, возможны случаи, когда в процессе выбега доля статического напора уменьшается вследствие работы паросбросных устройств или из-за некомпенсируемой течи. Это приводит к изменению входящих в выражения для момента сопротивления и подачи (96) параметров
и способствует увеличению длительности производительной работы таких насосов.
§ 16. Последовательность расчета совместного выбега
Расчет состоит в построении методом последовательных интервалов кривой выбега
по формуле (81) и в определении подачи насосных агрегатов по формулам (95), (96). Для этого, задавшись исходной номинальной частотой вращения n=1 и допустимым приращением частоты вращения ∆n, определяют по формуле (81) интервал времени ∆t, через который будет достигнуто искомое приращение частоты вращения. Входящий в эту формулу избыточный момент определяется по формулам (83)—(94).
Одним из существенных вопросов, определяющих точность расчета кривой выбега, является выбор допустимого интервала изменения частоты вращения в формуле (81). Проведенные вычисления с разными значениями
в пределах от 0,001 до 0,2 и сравнение со строгими методами исследования выбега показали, что при расчете выбега как из исходного двигательного режима, так и из генераторного на нисходящем участке вполне допустимо принять
=—0,02 во всем диапазоне частот вращения.
При выбеге из исходного генераторного режима начальный участок от п=1,0 до максимального значения п следует рассчитывать при ∆n=0,01. Приближение к точке перегиба определяется по уменьшению
до нуля.
Для исключения неопределенности, связанной с делением на нуль в формуле (81), рекомендуется после нахождения nмакc и соответствующего ему значения времени tмакc положить 
=0, найти соответствующее значение избыточного тормозного момента
задаться допустимым на нисходящем участке кривой n приращением
= —0,02, по формуле (81) определить Δt и продолжать дальнейший расчет, считая координаты
за исходные.
при выбеге из генераторного режима
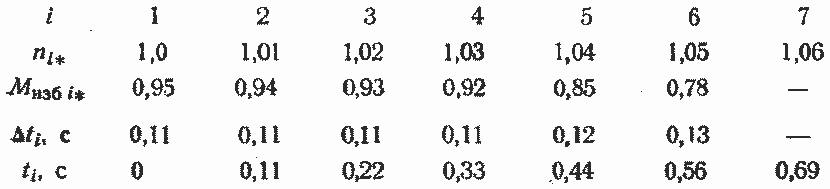
при выбеге из двигательного режима
