Практически важным является случай, когда реактивность реактора изменяется не скачком, а зависит от времени. Например, в процессе пуска реактор выводится из подкритического состояния медленным извлечением поглотителей и реактивность его возрастает в соответствии со скоростью перемещения регулирующих органов. В процессе работы реактора при переходе с одной мощности на другую реактивность также изменяется путем перемещения регулирующих стержней со сравнительно небольшой скоростью и ∆k зависит от времени.
При аварийной остановке реактора кроме стержней аварийной защиты обычно в активную зону вводятся и стержни управления (регулирующие и компенсирующие). В этом случае суммарное изменение реактивности определяется выражением
![]() (2.61)
(2.61)
где ∆kАЗ— реактивность стержней аварийной защиты; f(t) —изменение реактивности путем ввода стержней управления. При быстром введении стержней АЗ в активную зону можно считать, что ∆kАЗ изменяется скачком, а вторая составляющая зависит от времени.
При переменной реактивности уравнения кинетики имеют вид уравнений (2.59), (2.60) с той лишь разницей, что в них kэф зависит от времени. Решение системы в этом случае существенно усложняется, так как (2.59) и (2.60) становятся дифференциальными уравнениями с переменными коэффициентами.
Из таблицы видно, что через t=10 с с начала переходного процесса при линейном изменении реактивности со скоростью α=5·10-4 с s намного больше λ√l/α по крайней мере для графитовых и легководных реакторов. При этом реактивность в момент времени t=10 с достигает значения Δk=αt=5·10-3. Как видно, избыточная реактивность к этому моменту времени становится близкой к β и дальнейшее увеличение ее чревато опасными последствиями.
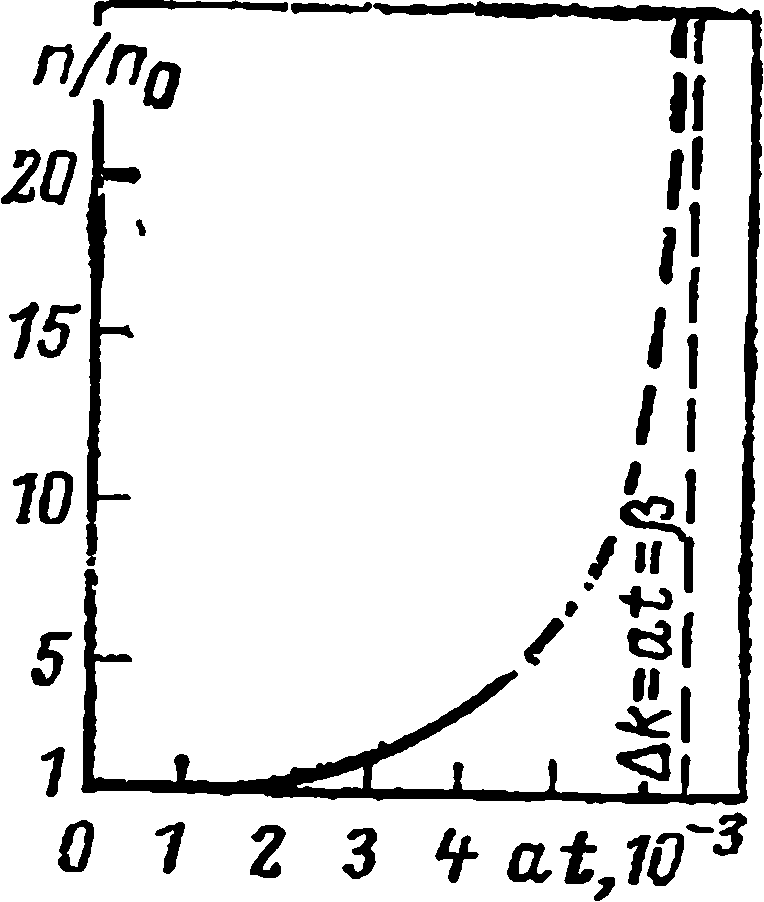
Решение уравнения (2.78) иллюстрируется рис. 2.9, на котором показано изменение плотности нейтронов во времени при линейном изменении реактивности Δβ=5·10-4t для l=10—3 с. Из рисунка видно, что сначала плотность нейтронов плавно возрастает, а при приближении ∆k к β резко возрастает. При Δk=β реактор достигает мгновенной критичности. Это еще раз свидетельствует о том, что подъем мощности реактора должен производиться при избыточной реактивности Δk<β.
Уравнение (2.76) можно решить при m=2; 3 и т. д., тогда величина а будет равна соответственно 2,5·10-4; 1,65-10"4 и т. д. При этом очевидно, что с увеличением m скорость изменения реактивности уменьшается и переходный процесс замедляется. Что же касается громоздкости вычислений, то она при этом существенно возрастает.
Решение уравнений кинетики (2.59) и (2.60) для различных скоростей линейного изменения реактивности ∆k=∆a с учетом одной средневзвешенной группы или шести групп запаздывающих нейтронов для l=10-3 с и l=10-4 с проведено на ЭВМ и показано на рис. 2.10 и 2.11. Напомним, что в этом случае реактор в начальный момент времени (при t=0) находится в критическом состоянии и в уравнении (2.59) внешним источником можно пренебречь. Заметим, что результаты приближенного аналитического решения уравнений кинетики, показанные на рис. 2.9 с использованием (2.78), хорошо согласуются с решением уравнений кинетики на ЭВМ (рис. 2.10,α, кривая при α=5·10-4 с-1).
Из графиков на рис. 2.10 и 2.11 видно значительное расслоение кривых изменения плотности нейтронов в зависимости от скорости линейного увеличения реактивности. Уменьшение скорости изменения реактивности приводит к тому, что при достижении одного и того же значения ∆k плотность нейтронов соответствует более высокому значению. Это становится особенно существенным при Δk>0,5β. Так, уменьшение скорости линейного изменения реактивности в 10 раз приводит к увеличению плотности нейтронов при ∆k=at=5·10-3 примерно на три порядка.
Приближенное решение уравнений кинетики (с учетом одной средневзвешенной группы запаздывающих нейтронов) по сравнению с решением полной системы (с учетом шести групп) дает, так же как это было и при скачкообразном изменении реактивности, заниженный результат.
Рис. 2.9. Изменение плотности нейтронов во времени при линейном росте реактивности
При этом при значениях Δk=αt<0,5β разница несущественна, а при ∆k>0,5β она возрастает.
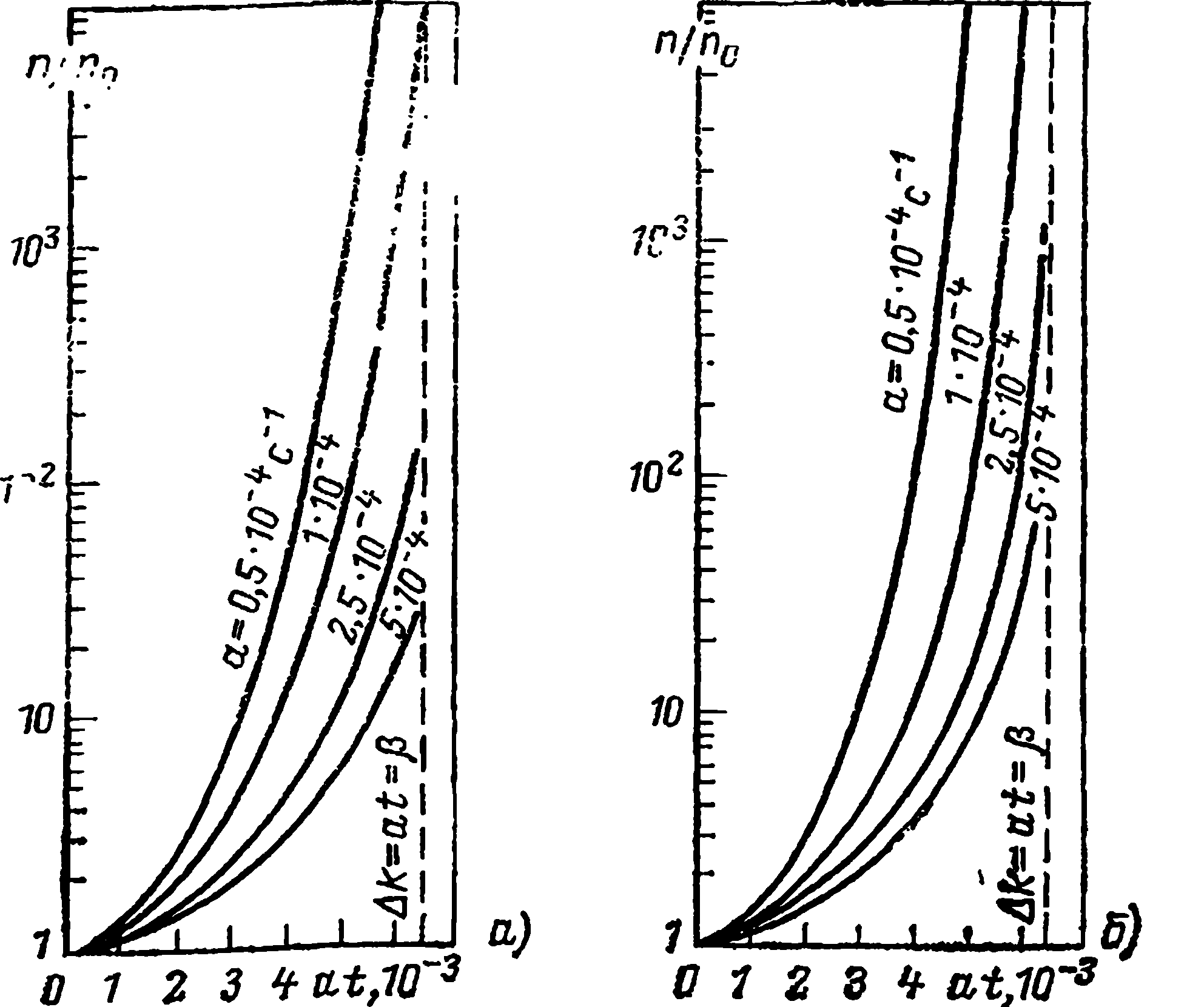
Рис 2.10. Изменение плотности нейтронов в зависимости от скорости линейного роста реактивности (решение уравнений кинетики при одной средневзвешенной группе запаздывающих нейтронов):
a-l=10-3 с; б — l=10-4 с
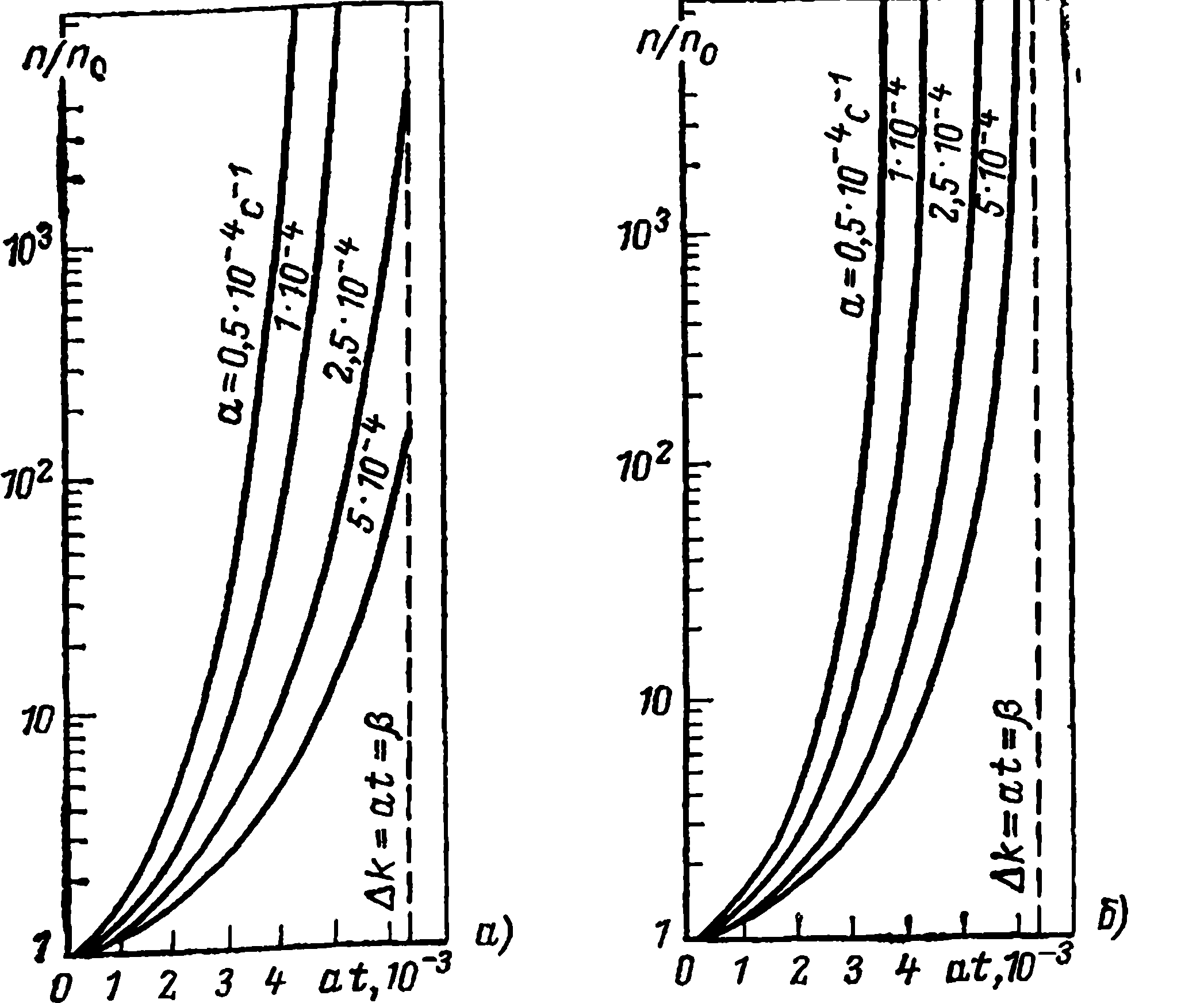
Рис. 2.11. Изменение плотности нейтронов в зависимости от скорости линейного роста реактивности (решение уравнений кинетики с шестью группами запаздывающих нейтронов): а=l-10-3 с; б = l-10-4 с
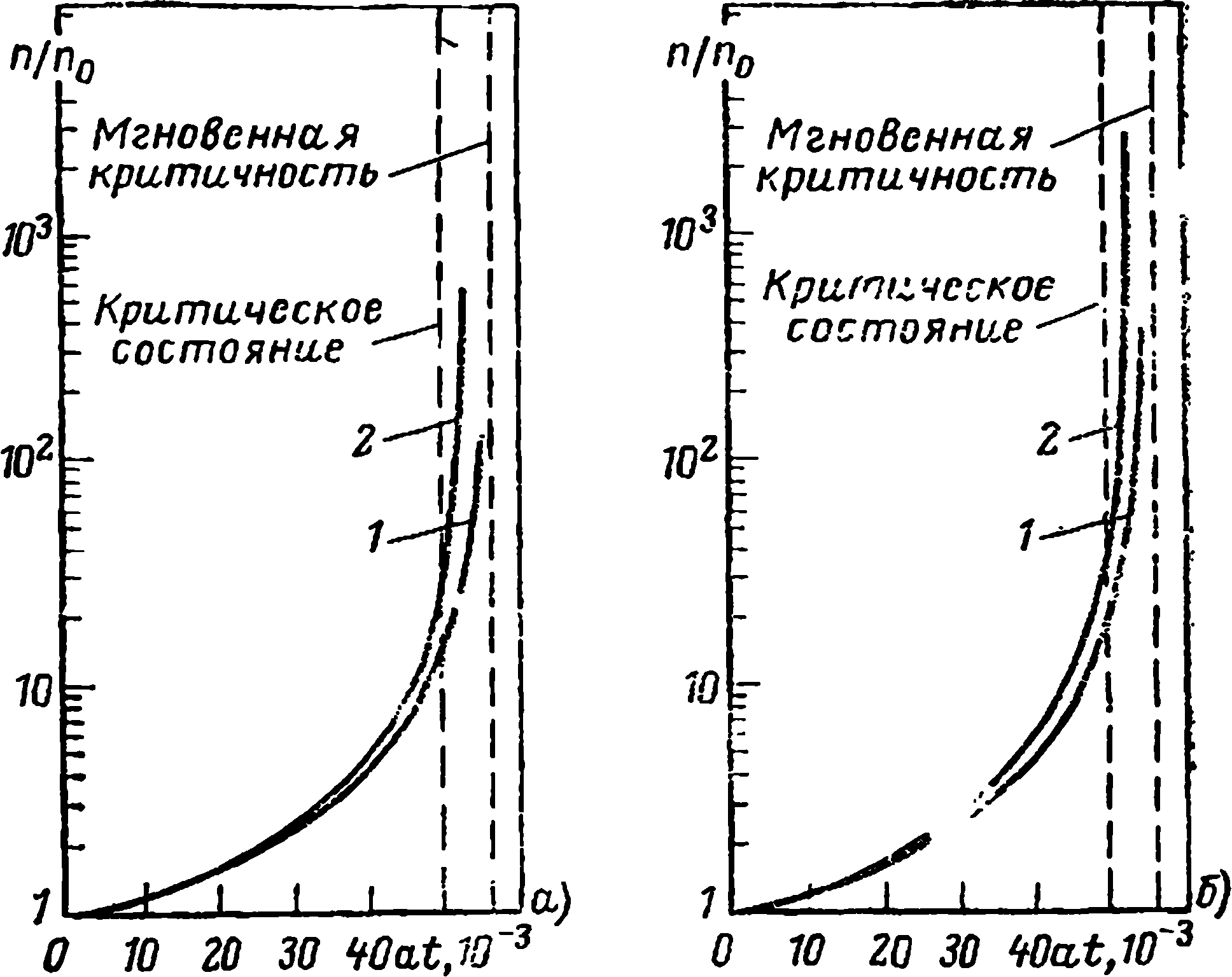
Рис. 2.12. Изменение плотности нейтронов при выводе реактора из подкритического состояния при линейном изменении реактивности с различной скоростью (kэф=0,95+аt, l=10-3 с):
a — одна средневзвешенная группа; б — шесть групп запаздывающих нейтронов; 1—а— —5-10 с-4; 2 — а=0,5-10-4 с-1
Влияние времени жизни мгновенных нейтронов l видно из сопоставления графиков на рис. 2.10 и 2.11. Уменьшение времени жизни приводит к заметному возрастанию скорости разгона при Δk=αt>0,5β, что вполне согласуется с графиками на рис. 2.2.
Изменение плотности нейтронов при выводе реактора из подкритического состояния в критическое и затем надкритическое при линейном изменении реактивности показано на рис. 2.12. При этом плотность нейтронов n в начальный момент времени (при t=0), определяемая из системы уравнений (2.59), (2.60) с использованием начальных условий dn/dt=0 и dCi/dt= 0, равна
![]() (2.83)
(2.83)
и зависит от глубины подкритичности (1—kэф) и мощности внешнего источника 5.
В данном случае нас не будет интересовать абсолютное значение п0 в начальный момент времени. Как видно из рис. 2.12, при выводе реактора из подкритического состояния в критическое плотность нейтронов изменяется сравнительно плавно. При этом чем выше скорость изменения реактивности, тем при меньшей плотности нейтронов реактор достигает критического состояния. При выходе реактора в надкритическое состояние скорость возрастания плотности нейтронов существенно увеличивается. Из сравнения графиков (рис. 2.12,а и б) видно, что приближенное решение системы уравнений дает заниженное значение плотности нейтронов по сравнению с точным решением.
На рис. 2.13 показано изменение плотности нейтронов при выводе реактора из подкритического состояния для различных начальных значений подкритичности и одинаковой скорости линейного изменения реактивности.
Рис. 2.13. Изменение плотности нейтронов при выводе реактора из подкритического состояния со скоростью α=5·10-4 с-1 при различных начальных значениях реактивности (решение уравнений кинетики для одной средневзвешенной группы запаздывающих нейтронов при l=10-3 с):
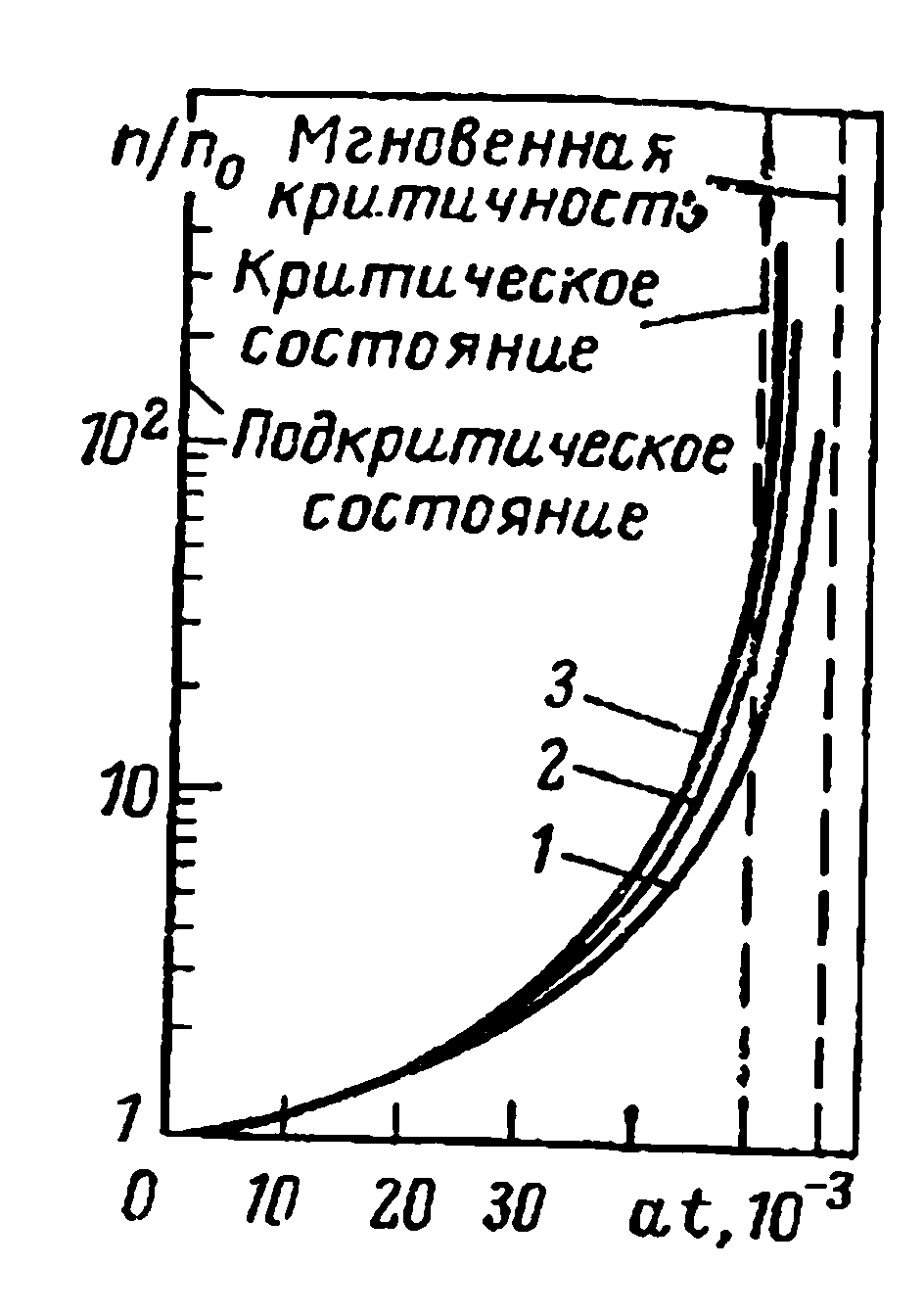
l — kэф=0,95+аt; 2 — кэф=0,9+at; 3 — kэф=0,8+аt
Из рисунка видно, что чем глубже начальная подкритичность, тем в больше раз возрастает плотность нейтронов к моменту вывода реактора в критическое состояние по сравнению с начальной плотностью. Однако следует учесть, что при более глубокой подкритичности начальная плотность нейтронов п0 меньше. Так, в данном примере начальная подкритичность, соответствующая кривым 2 и 3 на рис. 2.13, в 2 и 4 раза ниже по отношению к начальной подкритичности, соответствующей кривой 1 на этом рисунке. В этом случае, как следует из (2.83), при всех прочих равных условиях, что имеет место в данном примере, начальная плотность нейтронов соответственно в 2—4 раза ниже, чем для кривой 1. А так как скорость линейного роста реактивности одинакова для всех трех случаев, то и относительная плотность нейтронов при выходе в критическое состояние для кривых 2 и 3 соответственно в 2 и 4 раза выше, чем для кривой L В данном случае (рис. 2.13) относительная плотность нейтронов п/п0 в момент достижения критического состояния равна для кривых 1, 2 и 3 соответственно 15, 30 и 60, т. е. плотность нейтронов по отношению к начальной возросла в 15, 30 и 60 раз.
ЗАКЛЮЧЕНИЕ
Анализ переходных процессов показывает, что ядерный реактор весьма быстро реагирует на отклонения реактивности от критического состояния. Наличие запаздывающих нейтронов позволяет осуществлять переходные процессы с вполне допустимой скоростью. При этом следует иметь в виду, что положительная избыточная реактивность должна быть заметно меньше суммарной эффективной доли запаздывающих нейтронов. В противном случае, если избыточная реактивность равна или больше βэф, переходный процесс будет определяться практически только мгновенными нейтронами и пойдет весьма быстро, и реактор станет неуправляемым. Исходя из этого формулируются основные требования к органам регулирования реактора и всей схеме управления.
Наиболее ответственным режимом работы является вывод реактора из подкритического состояния в критическое и дальнейшее увеличение мощности до необходимого уровня. С помощью регулирующих органов (обычно регулирующих стержней) реактор доводится до критического состояния, после чего задается приемлемая избыточная реактивность и реактор выводится на заданный уровень мощности. По достижении последней избыточная реактивность компенсируется.
Ввод и вывод избыточной реактивности осуществляется соответственно выведением стержней регулирования из активной зоны реактора или введением их в активную зону.
Вывод стержней регулирования при пуске реактора производится не непрерывно, а отдельными «шагами». В пределах каждого шага реактивность линейно возрастает на величину Δk<β, что предотвращает возможность выхода реактора в мгновенную критичность. После каждого очередного шага определяется период реактора из соотношения
![]()
(2.84)
где Т — период реактора. Выражение (2.84) следует из (2.1) и (2.5). После очередного шага по изменению реактивности определяется величина dn/di. Если после некоторой выдержки dn/dt=0, то, как следует из (2.84), Т=∞ и реактор находится либо в подкритическом состоянии с новым уровнем плотности нейтронов — более высоким по сравнению с плотностью нейтронов до вывода стержня на данном шаге, либо уже достиг критического состояния. Если же dnjdt>0, то Т становится конечной величиной и мощность реактора начинает увеличиваться с приемлемой скоростью, так как в пределах каждого шага реактивность увеличивается обычно на величину Δk≤0,5β.

