Общие сведения. Использование современной вычислительной техники дает возможность исследовать сложные динамические процессы, происходящие в ядерных реакторах и энергетических установках в целом: переходные процессы при различного рода возмущениях, устойчивость ЯЭУ, распределение потока нейтронов и поля температур в реакторе, а также определять характеристики систем регулирования ЯЭУ.
Быстрые переходные процессы в реакторе характеризуются временами от долей секунд до минут. Первые обычно рассматриваются как скачки и характерны для аварийных выключений, вторые относятся к области рабочих переходных процессов, например переход с одного уровня мощности на другой. При исследовании пусковых режимов определяются характер изменения мощности (плотности нейтронов, температуры, расхода); наилучшая последовательность операций при пуске для исключения опасных скоростей разгона. Анализ рабочих режимов позволяет определить поведение уровня мощности по возмущениям реактивности и другим параметрам, изучить переходные процессы при саморегулировании. Особенно большое значение имеет изучение аварийных режимов, исследование аварийного расхолаживания после срабатывания аварийной защиты.
Медленные переходные процессы характеризуются временами от нескольких часов до нескольких лет. Сюда относятся процессы, связанные с выгоранием, отравлением, шлакованием. Это задачи по изучению изменения изотопного состава в твэлах за время кампании, отравления реактора продуктами деления, пространственной ксеноновой нестабильности, а также по изучению отравления ксеноном при останове реактора и по выбору оптимального режима останова.
При исследовании работы системы регулирования изучаются вопросы оптимального коэффициента усиления системы автоматического регулирования, глубины обратных связей, поведения регулятора при воздействии различных возмущений, отыскания оптимальных параметров настройки основных регуляторов, определения необходимого времени срабатывания системы аварийной защиты, а также «веса» аварийных стержней по реактивности.
При исследовании устойчивости ядерного реактора учитываются как внутренние обратные связи, обусловленные температурными и плотностными эффектами реактивности и ксеноновым отравлением, так и внешние обратные связи систем автоматического регулирования.
Ниже рассматриваются задачи моделирования кинетики реакторов при внесении возмущений по реактивности и переходных процессов в связи с изменением изотопного состава.
Модель кинетики реактора с одной средневзвешенной группой запаздывающих нейтронов. Рассмотрим точечную модель реактора. Уравнения кинетики с учетом одной средневзвешенной группы запаздывающих нейтронов и в отсутствие внешнего источника в соответствии с (2.59) и (2.60) можно записать в следующем виде:

Решение задачи будем проводить на АВМ. Преобразуем исходные уравнения к удобному для реализации на машине виду: 
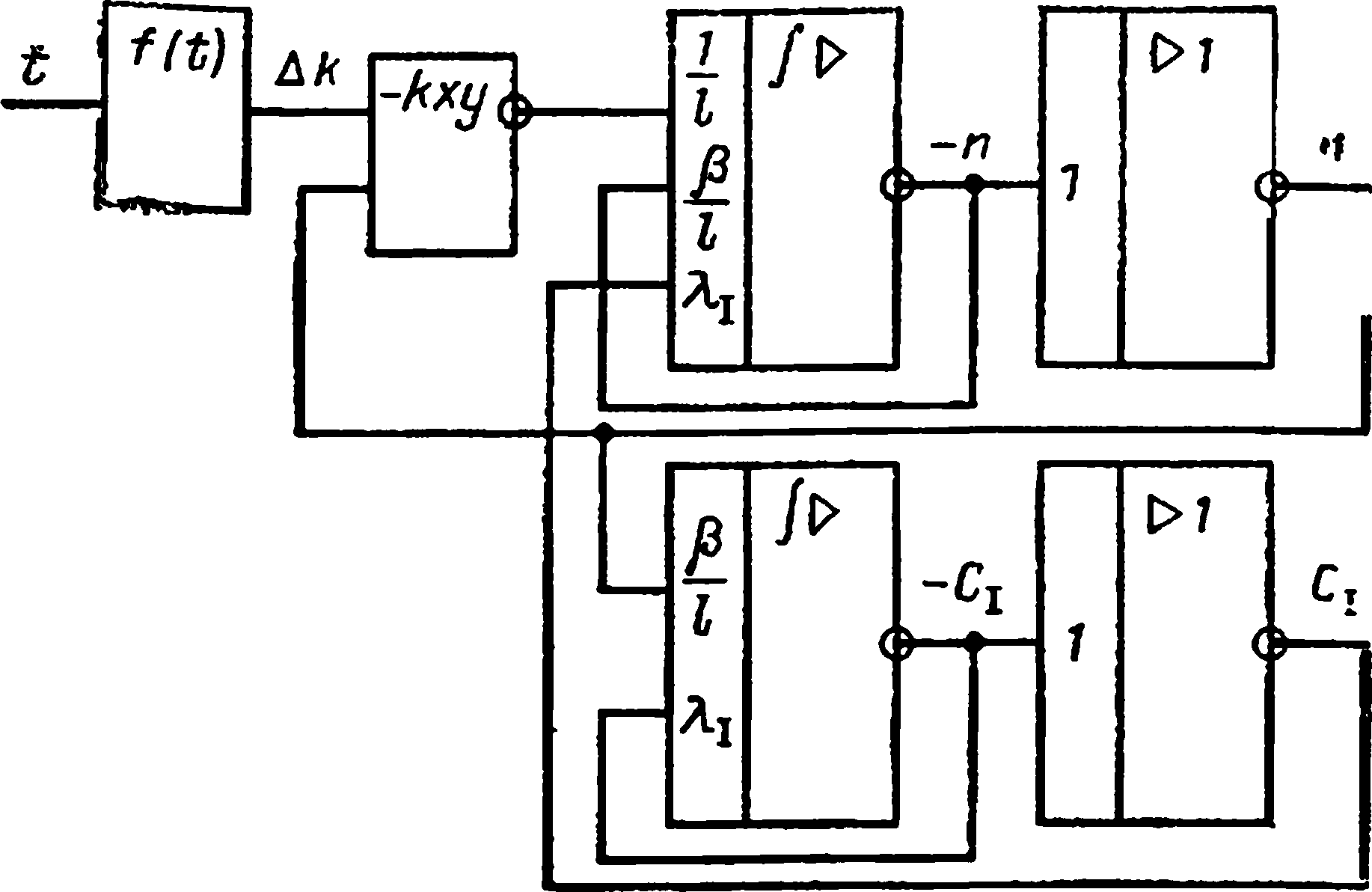
Рис. 7.12. Структурная схема модели кинетики реактора
Принимаем избыточную реактивность М функцией от времени.
Структурная схема для данной системы уравнений показана на рис. 7.12.
Принимая максимальные значения зависимых переменных nmах, Ci max и ∆kmax; определяем по (7.4) их масштабы тп, тс1 , m∆k.
Коммутационная схема, соответствующая структурной схеме, изображена на рис. 7.13.
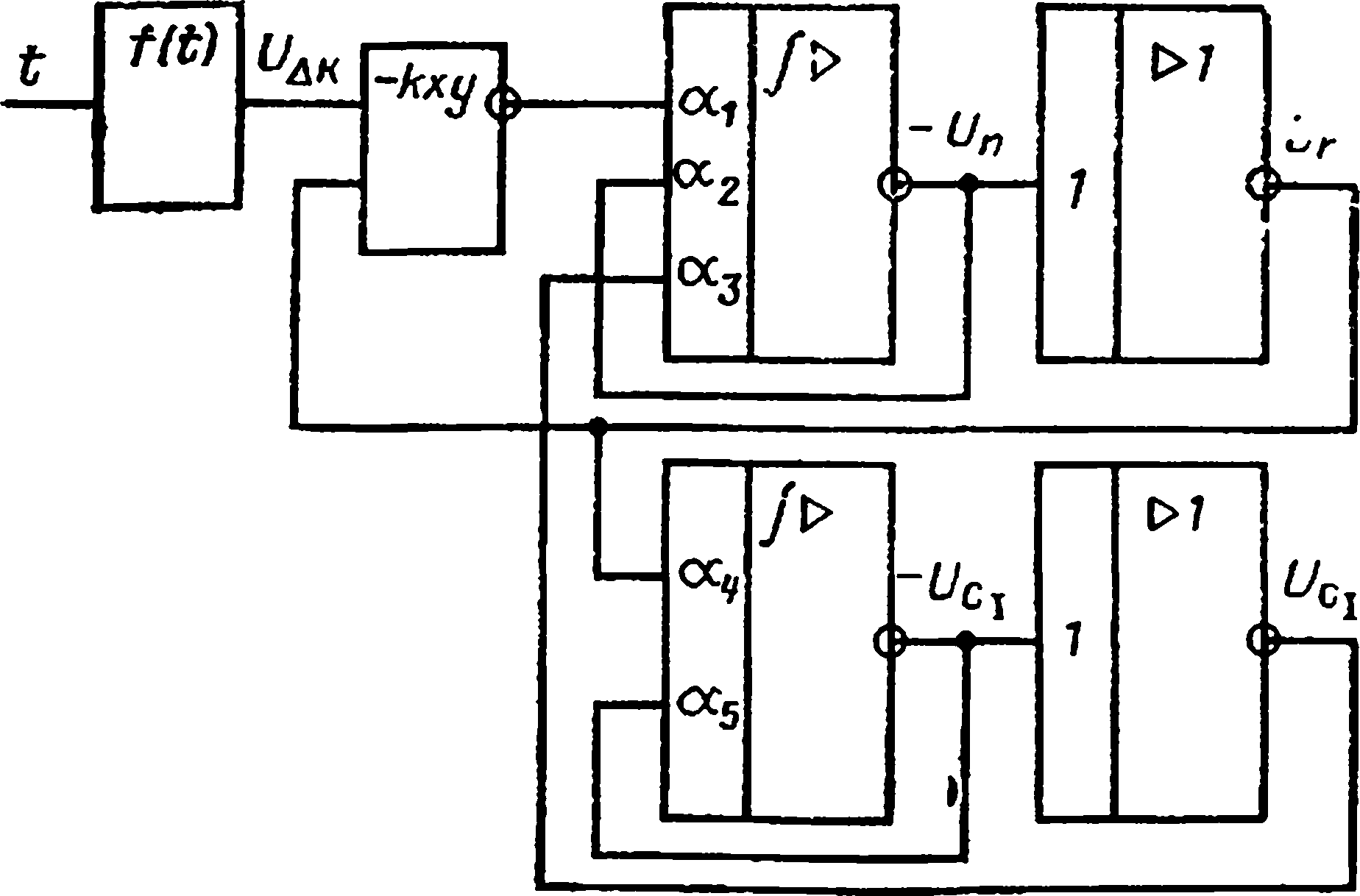
Рис. 7.13. Коммутационная схема модели кинетики реактора.
По (7.8) определяем коэффициенты передачи (масштабные коэффициенты) интегросумматоров. Они имеют вид: ![]()
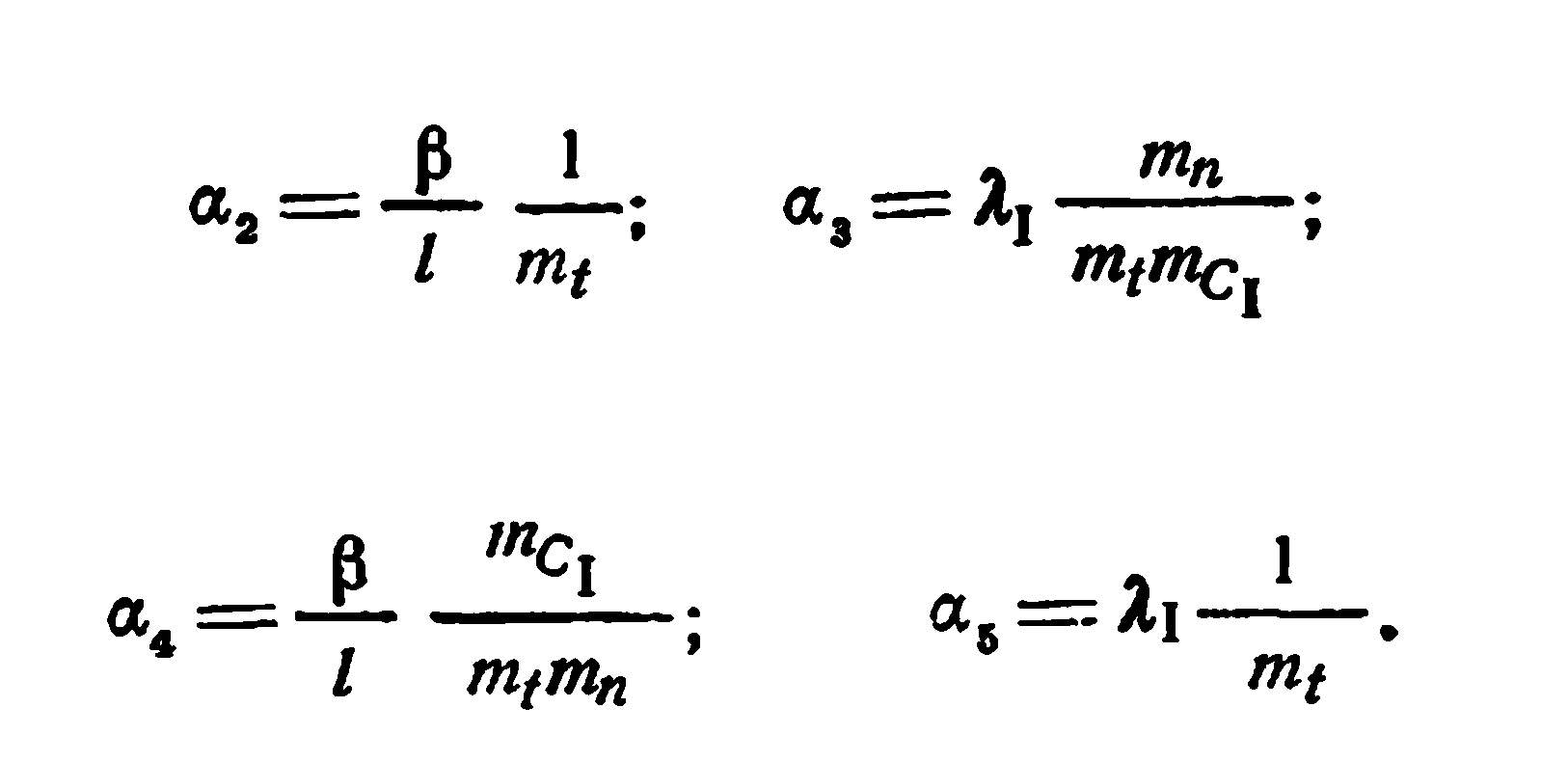
Так как процесс, описываемый данной моделью, не имеет взрывного характера, но в то же время протекает достаточно быстро, целесообразно выбрать масштаб времени mt=1.
Начальные условия Un0 и Uc10 определяются исходя из соотношений Un0=mnn0 и Uc10 = mci C10, где n0 и С10 — начальные значения плотности нейтронов и концентрации ядер-предшественников запаздывающих нейтронов.
В этом заключается подготовка задачи для решения на АВМ. Порядок дальнейшей работы следующий: набирают на наборном поле машины коммутационную схему, выставляют масштабные коэффициенты и начальные условия; в режиме решения задачи регистрируют изменения физических величин во времени измерительными и записывающими приборами при различных вариантах изменения реактивности.
Характер изменения плотности нейтронов во времени для скачкообразного изменения реактивности показан на рис. 2.4 и 2.6, а для линейного — на рис. 2.9.
Решение на АВМ более корректной математической модели кинетики реактора с шестью группами запаздывающих нейтронов производится аналогичным образом и требует использования лишь дополнительного числа интегросумматоров и инверторов.
Модель кинетики реактора с одной средневзвешенной группой запаздывающих нейтронов и обратными температурными связями по реактивности.
Особенностью ядерного реактора является тесная взаимосвязь физических и тепловых характеристик. Изменение температуры компонентов активной зоны приводит к изменению реактивности реактора. При этом из условий устойчивости и безопасности работы активная зона реактора конструируется так, чтобы температурный коэффициент реактивности на всех уровнях мощности и во всем диапазоне времени работы реактора по возможности был отрицательным.
Будем рассматривать ядерный реактор как динамическую систему с безынерционной обратной связью, допускающей наиболее простое математическое описание. Такое описание пригодно для анализа динамики достаточно медленных процессов, при которых изменения температур или плотностей различных сред реактора успевают следовать за изменениями нейтронной мощности.
Рассмотрим точечную модель реактора с одной группой запаздывающих нейтронов в предположении, что реактивность зависит от температур топлива и теплоносителя по линейному закону. Система уравнений динамики имеет вид:

где mu, сu, V — масса, теплоемкость и объем топлива; Ef — энергия, выделяемая в одном акте деления; v — средняя скорость нейтронов; — макроскопическое сечение деления урана; k — коэффициент теплопередачи от топлива к теплоносителю; su — площадь поверхности тепловыделяющих элементов; GT — расход теплоносителя; mт, ст — масса и теплоемкость теплоносителя в активной зоне; θт, θu — средние температуры теплоносителя и топлива по активной зоне; αт, αu— температурные коэффициенты реактивности по теплоносителю и топливу; ∆kвозм— возмущение реактивности.
Решение данной модели проведем на ЦВМ с использованием алгоритмического языка ANSI FORTRAN IV.
Программа состоит из головного блока и трех подпрограмм: RKGS, FCT и OUTP. Головной блок предназначен только для ввода исходных данных. Все основные вычисления производятся в подпрограммах RKGS и FCT. Вывод результатов расчетов осуществляется подпрограммой OUTP.
При разработке программы для лабораторных работ большое внимание было уделено вопросам удобства ввода и вывода данных.
Для решения системы дифференциальных уравнений был использован метод численного интегрирования Рунгс — Хейна — Кутта четвертого порядка. Стандартная подпрограмма RKGS, реализующая данный метод, в тексте программы не приведена.
На рис. 7.14 представлена схема алгоритма расчета модели, а в табл. 7.1—текст программы.
Характерные кривые переходных процессов при скачкообразном изменении реактивности, полученные на основании рассмотренной модели, показаны на рис. 7.15. Наличие отрицательной обратной связи, как видно из графиков, является стабилизирующим фактором и при изменении реактивности приводит к самопроизвольному переходу реактора на новый стационарный уровень мощности.
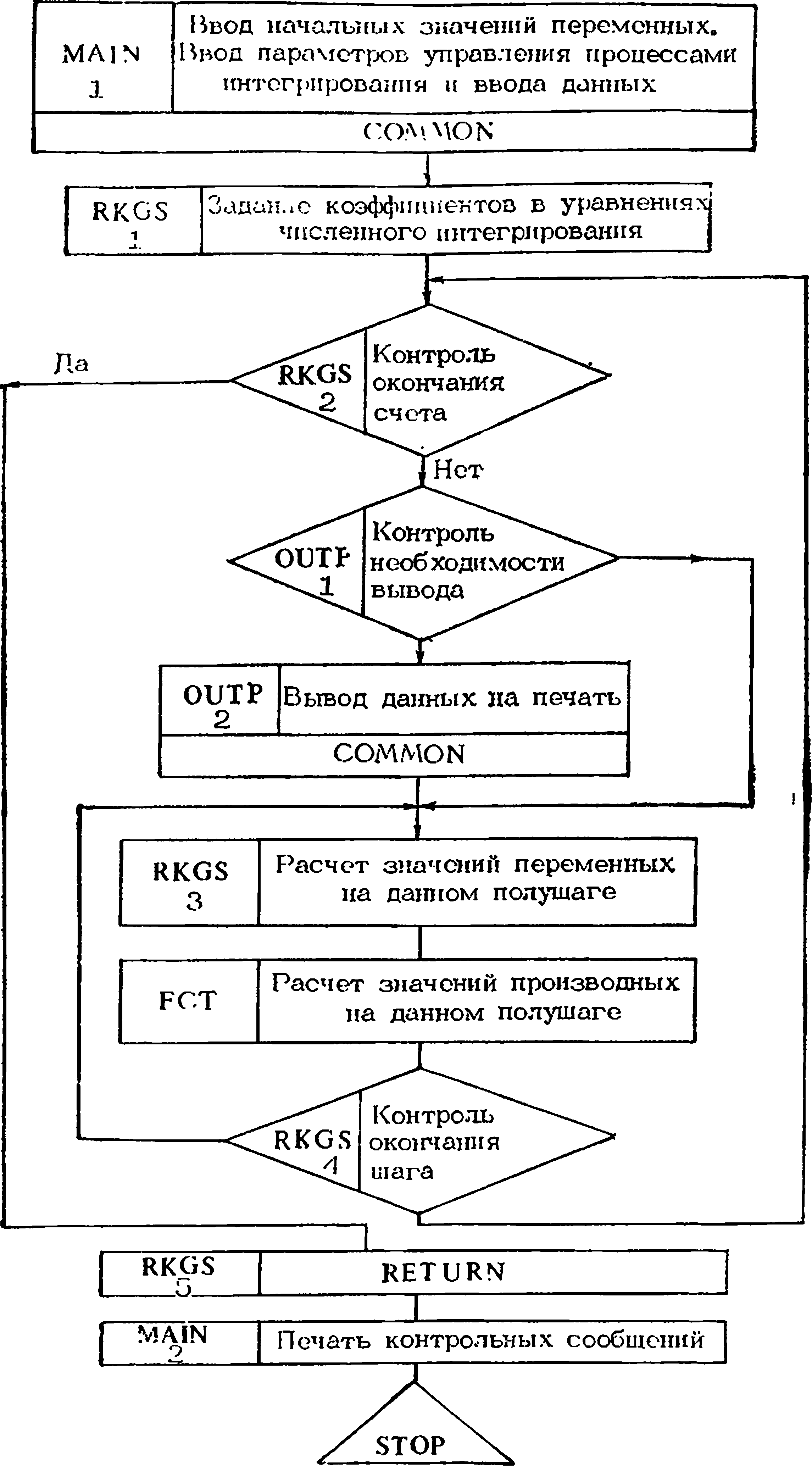
Рис. 7.14. Схема алгоритма расчета модели кинетики реактора с температурными обратными связями по реактивности на ЦВМ
Таблица 7.1. Текст программы


Модель отравления реактора ксеноном. При переходных режимах работы реактора, а также в конце кампании, когда запас реактивности невелик, влияние отравления ксеноном на реактивность реактора может стать столь существенным, что приведет к его временной неработоспособности (реактивность реактора на какой-то промежуток времени станет отрицательной и некомпенсируемой). В первую очередь эта проблема касается транспортных установок, требование к маневренности которых является одним из важнейших условий. Для стационарных реакторов переход с

Рис. 7.15. Изменение плотности нейтронов при наличии обратной температурой связи:
I — при ρ0=2·10-2; 2 — при —3-10-3
одного уровня мощности на другой, а также останов реактора производят по специальным программам, рассчитанным на минимум переотравления. В связи с этим моделирование процесса отравления приобретает особое значение.
Система уравнений, определяющая отравление реактора ксеноном в точечном приближении, состоит из (3.29), (3.34) и (3.39):


Рис. 7.16. Структурная схема модели отравления реактора ксеноном
![]()
Решение математической модели проведем на АВМ. Исходные уравнения без дополнительных математических преобразований вполне удобны для реализации на машине.
Считаем плотность потока нейтронов Ф функцией от времени.
Структурная схема модели изображена на рис. 7.16.
Масштабы зависимых переменных тФ,и mq, исходя из максимальных значений Фmax, NXe тaх, N I max и qXe max, определим по формуле (7.4).
В соответствии с коммутационной схемой составляем структурную схему (рис. 7.17).
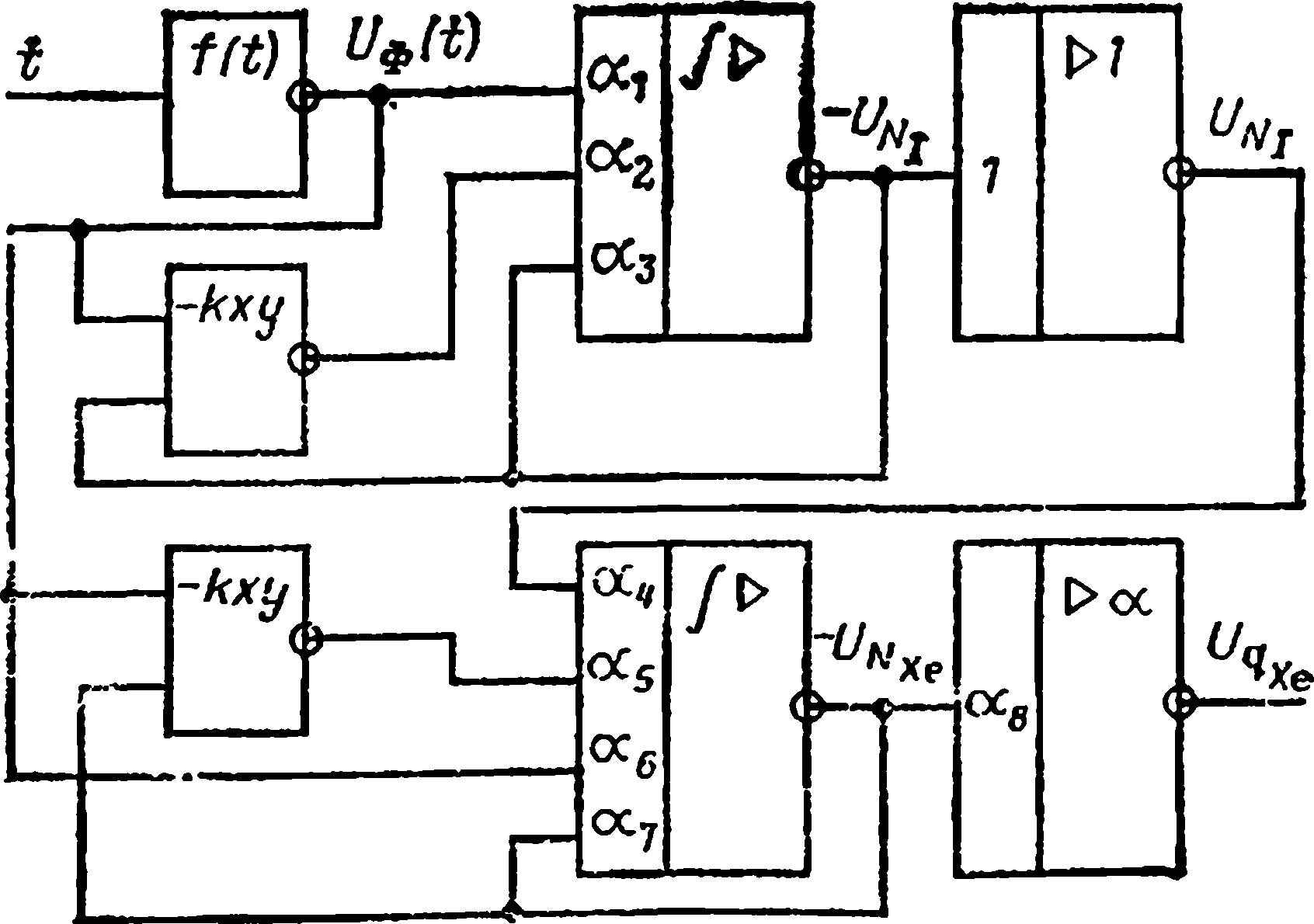
Рис. 7.17. Коммутационная схема модели отравления реактора ксеноном
7.4. ОШИБКИ ВЫЧИСЛЕНИЙ
Ошибкой называют разность между истинным значением переменной и ее значением, полученным при решении задачи на машине. Анализ ошибок в численном результате должен являться непременной составной частью любого вычисления независимо от того, производится это вычисление вручную или с помощью ЭВМ. Без анализа ошибок вычисления нельзя сказать что-либо определенное относительно точности результата.
В процессе численного решения на ЦВМ некоторой задачи приходится иметь дело с тремя основными видами ошибок: ошибками, содержащимися в исходной информации; ошибками, возникающими при ограничении бесконечного математического процесса конечным числом операций (ошибки ограничения); ошибками,возникающими в результате необходимости представлять число в виде конечной последовательности цифр (ошибки округления).
Ошибки в исходной информации возникают в результате неточности измерений, грубых просмотров или из-за невозможности представить необходимую величину конечной дробью. Эти ошибки определяют точность результата вычислений независимо от того, каким методом эти вычисления проводятся. Два других типа ошибок — ошибки ограничения и ошибки округления — определяются теми численными методами, которые были использованы для решения задачи.
Суммарная ошибка при вычислении на АВМ определяется совместным действием большого числа факторов. Главнейшие из них — ошибки операционных блоков, помехи и выбранный метод решения задачи.
Точность реального операционного блока определяется тремя типами ошибок. Ошибки первого типа — параметрические. Источниками параметрических ошибок являются технологические погрешности изготовления радиодеталей, из которых построен операционный блок.
Ошибки второго типа — структурные (конструктивные). Они вызваны конструктивными особенностями элементов, образующих реальный блок. В первую очередь эти ошибки связаны с операционными усилителями, которые в силу принципа действия их электронных схем не могут иметь бесконечно большой коэффициент усиления и не могут быть безынерционными.
Ошибки третьего типа — помехи. Они проявляются в отсутствие строгого соответствия машинной переменной и математической переменной.
Машинная переменная изменяется во времени более сложным и до какой-то степени случайным образом по сравнению с математической переменной. Источниками и причинами появления помех является большая совокупность неконтролируемых факторов, которые можно разделить на внешние и внутренние. К внешним факторам следует отнести нестабильность источников питания АВМ, влияние различных энергоемких электрических установок, питающихся от гой же электрической сети, что и данная АВМ, изменение температуры и влажности окружающей среды и т. д. Внутренние факторы связаны с возникновением помех, которые возникают внутри самой АВМ, в различных ее блоках. Эти помехи обусловлены флуктуациями электрических токов и напряжений. Кроме того, к внутренним факторам следует отнести взаимное электрическое влияние блоков АВМ в процессе работы машины.

