Механическими колебаниями или вибрацией называется чередование возрастания и убывания смещения точки механической системы, например машины или станка. Колебательными или вибрационными смещением, скоростью или ускорением вибрирующего тела называются мгновенные значения этих величин.
Вибрация вызывается возмущающей силой, которая возникает по различным причинам механического и электромагнитного характера.
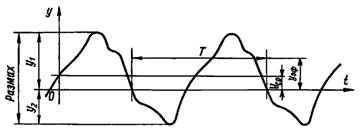
Рис. 1. Периодические колебания
При работе машины обычно имеет место периодическая вибрация, при которой определенные значения вибросмещения, виброскорости и виброускорения повторяются через одинаковые промежутки времени в одной и той же последовательности.
Частота / периодических колебаний (рис. 1), т. е. число повторяющихся циклов колебаний в секунду, измеряется в герцах:
где Т — период колебаний, равный наименьшему промежутку времени, через который повторяется цикл колебаний.
Размах периодических колебаний — абсолютное значение отклонения колебательной величины от одного крайнего значения до другого. При различных знаках крайних значений колебательных величин размах равен сумме их абсолютных значений (рис. 1).
Периодические колебания любой формы характеризуются некоторыми средними значениями колебательных величин за период.
Средним значением называется среднее арифметическое всех мгновенных значений колебательной величины за период Т (рис. 1).
Действующим или эффективным значением называется корень квадратный из среднего квадратического значения всех мгновенных значений колебательной величины за период Т (рис 1).
Эквивалентным значением называется эффективное значение колебательной величины, умноженное на -ѵ2.
Периодические колебания вибрационных величин (смещение, скорость, ускорение), изменяющиеся во времени по закону синуса (или косинуса), называются гармоническими (рис. 2):
(1)
у=А sin (а>/+40,
(2)
261
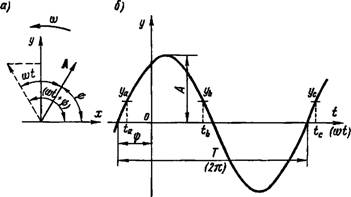
Рис. 2. Гармонические колебания
где А — амплитуда, равная наибольшему абсолютному значению величины у\ i — время от начала отсчета; (cd/+i|>) — фазовый угол; ф — начальный фазовый угол; о> — угловая частота.
Наряду с графическим изображением в прямоугольных координатах (рис. 2, б) гармонические колебания изображаются также условным вектором, длина которого равна в определенном масштабе амплитуде колебаний; этот вектор вращается против часовой стрелки с угловой частотой ю. При этом подразумевается, что проекция вектора на ось Оу в любой момент времени равна по величине и направлению соответствующему мгновенному значению колебательной величины (рис. 2, а).
В дальнейшем для сокращения будем говорить «вектор смещения», «вектор ускорения» и т. п. При этом нужно помнить, что имеется в виду вектор вращающийся, проекция которого изображает мгновенное значение рассматриваемой колебательной величины.
Применение векторных диаграмм существенно упрощает расчеты при выполнении работ по балансировке.
Фазой называется характеристика гармонических колебаний в данный момент, которая определяется не только мгновенным значением колебательной величины, но и направлением изменения этого значения. Например, в моменты времени /«, U и tc (рис. 2, б) все мгновенные значения уа, уь и ус равны по значению и знаку, но изменяются одинаково только значения в моменты времени ia и tCt отличающиеся друг от друга на полный период.
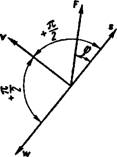
Рис. 3. Векторная диаграмма возмущающей силы F, вибрационного смещения s, скорости v и ускорения w
При совместном рассмотрении синхронных колебаний различных величин, т. е. гармонических колебаний одинаковой частоты, их изображают на одной векторной диаграмме.
Важной величиной, характеризующей соотношение различных синхронных колебаний, является сдвиг их одинаковых фаз во времени, который для сокращения называют просто сдвигом фаз.
Сдвиг фаз равен разности начальных фазовых углов и определяется на диаграмме углом между соответствующими векторами.
На диаграмме (рис. 3) в качестве примера изображены векторы гармонической возмущающей силы и вызываемых ею вибрационных величин — смещения s, скорости v и ускорения w, сдвиг фаз которых составляет я/2.

