4-7. ОСОБЕННОСТИ РАСЧЕТА ПРОВОДОВ И ШИН ПОДВЕСНЫХ (ОТКРЫТЫХ) ТОКОПРОВОДОВ
Общие положения. Подвесные токопроводы с гибкой или жесткой ошиновкой, расположенные на открытом воздухе, представляют собой по существу одну из модификаций воздушных линий электропередачи. Поэтому, естественно, методы механического расчета токоведущих частей подобных токопроводов в основном аналогичны методам, используемым при расчете проводов обычных воздушных линий, и методам, рекомендованным курсом сопротивления материалов для расчета, самонесущей балки с равномерной нагрузкой ее по всей длине между опорными точками (токопроводы с жесткой ошиновкой). Некоторые незначительные отличия в расчете в основном обусловлены лишь конструктивными параметрами токопровода (количество проводов в каждой фазе, конфигурация и количество токоведущих шин, наличие междуфазных и внутрифазовых распорок и т. п.).
Вполне очевидно, что приведенные выше соответствующие расчетные формулы для определения дополнительных нагрузок, вызываемых влиянием атмосферных явлений (ветер, гололед, температура воздуха) или фиксирующими устройствами на токопроводе, могут быть легко преобразованы применительно к конкретным условиям. Однако наряду с общепринятыми положениями механического расчета специфика работы подвесного открытого токопровода предопределила ряд особенностей его расчета. Основные из них для различных типов токопроводов с симметричным расположением фаз рассмотрены ниже. При этом наряду с апробированными решениями в части устройства подвесных токопроводов в заключение приведены некоторые предпосылки, касающиеся сооружения токопроводов из алюминиевых (или из алюминиевого сплава) шин трубчатого сечения в виде гибких провисающих нитей.
Токопроводы с гибкой ошиновкой. Как отмечалось выше, для устройства гибких токопроводов используются, как правило, алюминиевые провода крупных сечений (обычно до А-600), имеющие значение временного сопротивления разрыву 15 кГ/мм2. При этом согласно действующим ПУЭ максимально допускаемое напряжение в материале провода (по условиям его механической прочности) может быть принято равным:
С другой стороны, допускаемая механическая нагрузка применяемых обычно для токопроводов подвесных изоляторов (в частности, для натяжных гирлянд) с учетом нормируемого коэффициента запаса прочности составляет, как правило, от 2 500 до 4 000 кГ. Для того чтобы обеспечить полное использование физико-механических характеристик провода в многопроводной фазе, требуется скомплектовать многоцепную натяжную гирлянду изоляторов.
Действительно, нагрузка от тяжения по фазе токопровода, состоящей из четырех проводов марки А-600, составит
Приняв для данного случая изоляторы ПС-11, обладающие высокими физико-механическими свойствами, получим допускаемую нагрузку по одной цепи с учетом нормируемого коэффициента запаса прочности (k3an— = 2,7):
где Рг — гарантированная электромеханическая прочность изолятора, кГ.
Следовательно, число цепей в гирлянде по условиям механической прочности изоляторов
что определяет необходимость в данном случае в комплектовании пятицепной гирлянды изоляторов ПС-11, что, конечно, неприемлемо как по конструктивным соображениям, так и с технико-экономической точки зрения. Аналогичное положение создается и при использовании для комплектования гирлянд стандартной линейной арматуры. Таким образом, учитывая изложенное выше, а также приняв в качестве наиболее рационального количество цепей в натяжной гирлянде (по конструктивным соображениям) не более 2—3, можно получить величину напряжения амакс для каждого конкретного случая из формулы
(4-49)
где Fсум — суммарное сечение проводов в фазе, мм2.
С другой стороны, немаловажным фактором, с которым следует считаться при выборе максимально допускаемого напряжения, является несущая способность применяемых опорных конструкций. Исходя из этого, величину Тмакс определяют, сообразуясь с необходимостью более рационального выполнения опор и фундаментов, на основании соответствующих технико-экономических расчетов и сопоставлений. Следует иметь в виду, что значительные нагрузки от тяжения по проводам (особенно для угловых и концевых опор) приводят к необходимости создания чрезмерно тяжелых и сложных конструкций, что вызывает существенные перерасходы материалов, удорожает стоимость сооружения, осложняет технологические процессы при производстве строительно-монтажных работ.
Как показала практика проектирования, суммарное тяжение по проводам каждой фазы двухцепного токопровода, как правило, не должно превышать 8—10 Т. Здесь следует отметить, что в подавляющем большинстве случаев величина , полученная из (4-49), обычно отвечает поставленным выше условиям рационального выполнения опорных конструкций. Как уже отмечалось, одной из конструктивных особенностей гибкого токопровода является наличие в пролете на проводах токопровода фиксирующих устройств (внутрифазных и междуфазных распорок), количество и места установки которых определяются расчетом электродинамической устойчивости при протекании токов короткого замыкания. В этой связи механический расчет проводов токопровода должен учитывать дополнительные нагрузки от веса распорок, которые в ряде случаев (в частности, на головных участках токопровода) существенно влияют на работу проводов в пролете.
Дополнительные нагрузки на провода фазы от веса внутрифазных распорок, учитывая сравнительно небольшой единичный вес последних по сравнению с пучком проводов фазы, а также характер их расположения в пролете допускается принимать равномерно распределенными по всей длине пролета токопровода.
Междуфазные распорки, имеющие, как правило, значительный единичный вес и располагаемые обычно в середине пролета либо на расстоянии 1/3 пролета от опор, в известной степени влияют на характер провисания провода, поскольку они представляют собой определенный вид сосредоточенной нагрузки.
Поэтому в этой части расчет должен выполняться, как правило, в соответствии с рекомендациями § 4-6 и [Л. 14]. При этом во всех случаях определение величины наибольшей стрелы провеса производится с учетом высшей температуры окружающего воздуха и добавочного нагрева провода током нагрузки, определяемым пропускной способностью проводов по условиям нагрева, т. е., как правило, при температуре не ниже 70° С.
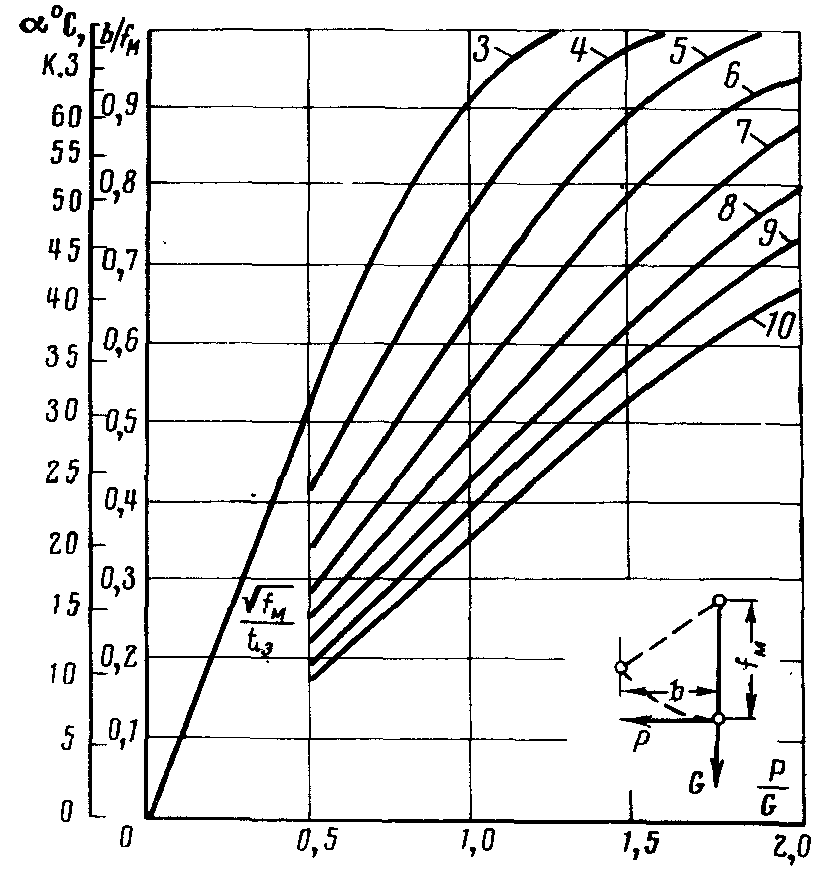
Рис. 4-13. Диаграмма для определения отклонений гибких шин под воздействием тока короткого замыкания (разработана инж. Н. Г. Гейниным).
Одним из основных элементов механического расчета подвесных токопроводов является расчет электродинамической устойчивости при протекании токов короткого замыкания. При этом для расчета на схлестывание проводов в пролете расчетным случаем является двухфазное короткое замыкание, при котором фазы, расположенные в одной горизонтальной плоскости, отклоняются под воздействием электродинамических усилий. После прекращения протекания токов короткого замыкания эти фазы, перемещаясь по инерции и проходя через первоначальное положение, соответствующее нормальному режиму работы токопровода, сближаются на расстояние, которое может оказаться недопустимым (менее 20 см), что может привести к серьезным повреждениям фаз токопровода.
Расчет выполняется в соответствии с изложенными ниже рекомендациями по известной диаграмме Гейнина [Л. 16] на рис. 4-13.
Некоторые предпосылки для расчета шин как гибких провисающих нитей. Токопроводы с жесткой ошиновкой находят все более широкое применение ь системах электроснабжения энергоемких предприятий, однако по сравнению с гибкими токопроводами они имеют ряд существенных недостатков. Одним из них является чрезвычайно высокая стоимость сооружения, в отдельных случаях превышающая более чем в 1,5—2 раза стоимость сооружения токопроводов с гибкой ошиновкой. Это объясняется не столько дорогостоящим проводниковым материалом, сколько малыми длинами пролетов L (обычно не более 25—35 м), требующих установки значительного количества опорных конструкций по трассе токопровода, что приводит к существенным расходам материалов. Кроме того, дополнительные производственные площади под опоры затрудняют, а иногда делают невозможным осуществление рациональных решений при размещении на генплане предприятия разного рода технологических коммуникаций и объектов, что отрицательно сказывается на технико-экономических показателях сооружения в целом.
В свою очередь токопроводы с гибкой ошиновкой, имеющие, как правило, удовлетворительные экономические показатели и приемлемые длины пролетов между опорами (порядка 60—80 м) с точки зрения монтажа проводов не удовлетворяют в полной мере современным требованиям индустриализации строительно-монтажных работ. С другой стороны, как показывают соответствующие исследования, этот тип токопроводов не может быть применен на предприятиях с агрессивными фракциями, приводящими к преждевременной коррозии голых многожильных алюминиевых проводов. В подобных условиях используются, как правило, токопроводы жесткого типа, выполненные из алюминиевых или из алюминиевого сплава шин, поверхность которых в процессе монтажа защищается антикоррозионным покрытием, например лаком. Учитывая изложенное, необходимо использовать для устройства токопроводов наиболее устойчивый к коррозии проводниковый материал (сортамент), сократить количество опорных конструкций увеличением длин расчетных пролетов и, таким образом, повысить технико-экономические и эксплуатационные показатели сооружения.
Соответствующие исследования и разработки (нашедшие в дальнейшем практическое применение в строительстве), выполнены инж. Г. А. Тартаковским. Целесообразность сооружения на отдельных участках трассы надземных трубопроводов из стальных труб, подвешиваемых на опорах в виде гибких провисающих нитей, делает возможным применение этих исследований при сооружении открытых подвесных токопроводов [Л. 13].
Поскольку методика расчета шин токопроводов в виде провисающих нитей находится в стадии теоретических разработок и требует в дальнейшем тщательных экспериментальных обоснований, здесь приведены лишь общие сведения и рекомендации, дающие возможность применить в практике проектирования и строительства подобные решения. Как показали соответствующие сопоставления, наиболее приемлемыми в качестве токоведущих шин в данном случае являются круглые трубы крупных сечений (4 000 мм2 и более), изготавливаемые из алюминиевого сплава АД31Т1 и имеющие предел прочности по ГОСТ 10552-67 не менее 2 000 кГ/см2.
Как показывают результаты многочисленных сопоставительных расчетов, величина
имеет значение лишь при расчете труб большого диаметра, обладающих высокими физико-механическими свойствами (в частности, при расчете стальных труб). Для применяемых в токопроводах труб из алюминиевого сплава, имеющих наибольший диаметр по ГОСТ =25 см, эта величина, имея большое абсолютное значение, несоизмеримое с единицей, может быть в формуле (4-61 а) взаимно сокращена. Таким образом, с достаточной для практических расчетов точностью выражение (4-61 а) может быть представлено в виде
(4-616)
При величине т равной или близкой к единице влияние жесткости на провисающую трубу очень мало, в связи с чем в практических расчетах ею можно пренебречь. При малых значениях т. (менее 0,92—0,95) жесткость оказывает существенное влияние на работу трубы в пролете, и с этим обстоятельством следует считаться. Из (4-616) можно заметить, что на величину коэффициента т для труб из одного и того же материала основное влияние оказывают длина пролета между точками подвеса (L=!2лг0) и диаметр трубы D1. В меньшей степени на величину т влияет стрела провеса fo. Диаметр трубы является в каждом случае постоянной величиной, поскольку он был предварительно определен в электрическом расчете токопровода.
Длина пролета между опорами (L=2x0) устанавливается, исходя из соображений достижения определенного экономического эффекта и должна, очевидно, иметь в 3—4 раза большие значения по сравнению с токопроводами жесткого типа, т. е. быть порядка 100—130 м. Стрела провеса принимается, исходя из условий обеспечения допускаемых напряжений в материале шин. а также предотвращения схлестывания последних в пролете в нормальном и аварийном режимах работы токопровода.
Напряжение растяжения стр и напряжение изгиба ав в середине пролета могут быть определены соответственно из формул
(4-62)
и 
(4-63)
Таким образом, увеличение стрелы провеса f0, естественно, приводит к уменьшению стр и увеличению сти. Оптимальная с точки зрения наименьшего суммарного напряжения в материале шины (стСум = (Тр + (Ти) стрела провеса может быть определена [JI. 13] по формуле
(4-64)
или, подставив в (4-64) постоянные значения у = = 2,75- Kh-3 кГ/см3 и £"=7,1 -105 кГ/см2, получим:
(4-64а)
Полученная из (4-64а)
стрела провеса f0 не всегда может быть принята в качестве исходной, поскольку в ряде случаев, имея значительную величину, она не является приемлемой с точки зрения схлестывания шин в пролете. Очевидно, что по этим условиям желательны по возможности меньшие значения fo (очевидно, в зависимости от пролета не более 2—3 м). По-видимому, в подобных случаях задача может быть решена следующим образом. Задавшись приемлемыми значениями стрелы провеса f0 и коэффициента т, используя (4-616) и решив последнее относительно х0, очевидно, можно получить оптимальное с точки зрения заданных условий значение длины пролета между опорами (L=2лг0):
Выше изложена лишь очень небольшая часть вопросов, связанных с расчетом трубчатых провисающих шин, которые предполагается использовать в качестве токоведущих элементов на подвесных открытых токопроводах. В частности, не рассмотрены влияние климатических условий на работу шин, устойчивость круговой формы сечения и защиты от вибрации, методология определения напряжений в опорных сечениях в местах закрепления труб на опорах и ряд других вопросов, освещение которых выходит за пределы объема и темы данной книги.
