КОСОЛАПОВ Ю. С.,
ПРОЦЕНКО Е. Ю.
РЕШЕНИЕ ЗАДАЧИ ОБ ОСЕСИММЕТРИЧНОМ ТЕЧЕНИИ ГАЗА В ВЕНЦЕ ТУРБОМАШИНЫ
Проведено осреднение стационарных уравнений движения идеального газа в форме Крокко, записанных в произвольной криволинейной системе координат. Уравнения, соответствующие модели течения в бесконечно густой решетке с тонкими лопатками, сведены к уравнению для функции тока (УФТ). краевые задачи для которого решались численно. Система конечно-разностных уравнений, получающихся в результате аппроксимации УФТ со вторым порядком, решалась явным методом переменных направлений. Приведены примеры расчетов дозвуковых течений газа в рабочем колесе осевого и центробежного компрессоров. Результаты работы сравниваются с экспериментальными и расчетными данными других авторов.
В настоящее время систематические расчеты пространственных течений в отдельных венцах турбомашины проводят, как правило, в рамках модели идеального газа [1-3]. В некоторых работах [4—5] при расчете таких течений влияние вязкости частично учитывается введением различных моделей пограничного слоя. Численное решение задачи о пространственном течении в многоступенчатой турбомашине даже в приближении идеального газа требует слишком больших времен счета. Поэтому обычно такие задачи ставятся для осредненных по окружной координате уравнений движения идеального газа [6—8]. Известно, что осредненные уравнения движения (ОУД) можно свести к одному нелинейному уравнению второго порядка в частных производных относительно функции тока [8]. Методы решения УФТ хорошо разработаны и позволяют получать численные решения значительно быстрее (на порядок и более), чем методы численного интегрирования уравнений Эйлера.
В данной работе проведено осреднение уравнений движения идеального газа в форме Крокко, записанных в произвольной криволинейной системе координат. Такая запись ОУД в отличие от записи ОУД в частных системах координат [6, 7] позволяет, не меняя вида уравнений, решать задачи о течении газа в различных геометрических областях (например, в венцах как осевых, так и центробежных турбомашин). ОУД, соответствующие модели течения в бесконечно густой решетке с тонкими лопатками, сведены к уравнению для функции тока (УФТ), краевые задачи для которого решались численно. Система конечно-разностных уравнений, получающихся в результате аппроксимации УФТ со вторым порядком, решалась явным методом переменных направлений [9]. Приведены примеры расчетов дозвуковых течений газа в рабочем колесе осевого и центробежного компрессоров. Результаты настоящей работы сравниваются с экспериментальными и расчетными данными других авторов.
Получение ОУД в форме Крокко. Осредним векторное уравнение Крокко. Во вращающейся системе координат оно имеет вид
 (1)
(1)

Приведем УФТ для осесимметричного течения в свободных от венцов кольцевых каналах. Для этого заметим, что уравнения, описывающие такие течения, могут быть получены осреднением по φ (в пределах от 0 до 2π) компонентов уравнения (1). Вид осредненных таким образом уравнений совпадает с видом уравнений (9) при Fξ=Fη=Fu=0. Положив в уравнении (9б) Fη=0 и выразив компоненты скоростей через производные от функции тока, получим
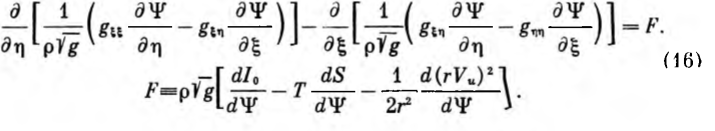
Заметим, что уравнения (15), (16) в цилиндрической системе координат (ξ=Z, η=r, φ=φ) совпадают с уравнениями, приведенными в [8].
Постановка и метод решения
Постановка и метод решения задачи о стационарном течении идеального газа через неподвижный или вращающийся венец турбомашины. На рис. 1, а представлено меридиональное сечение кольцевого канала турбомашины.
Заданы: верхняя и нижняя образующие канала, линии, соответствующие входному и выходному сечениям канала, проекции входных и выходных кромок венца. Каждая из подобластей ABDC, CDKE и EKLN физической плоскости отображаются на единичный квадрат в плоскости ξ, η (рис. 1,б). В областях ABDC и EKLN, не содержащих венец, решается УФТ (16), в области венца CDKE — УФТ (15).
Заданы: расход газа через канал — G и ω (для неподвижного венца ω= =0); на левой АВ и правой LN границах области соотношения между радиальной и осевой компонентами скорости; на входе распределения: I0=I0(r), S=S(r), Г=Г(r), (Г=rVu) или I0=I0(Ψ), S=S(T). Г=Г(Ψ); на нижней границе ACEN Ψ=0, а на верхней границе В1ЭКЕ — Т=С. Предполагается, что средняя межлопаточная поверхность тока совпадает со средней поверхностью лопатки, задаваемой уравнением φ=φ(z, r).
Для всех величин, входящих в УФТ, и в граничные условия выбраны следующие масштабы: для скорости и плотности — их критические значения а., р. вычисленные по параметрам торможения на входе в канал в неподвижной системе координат; для длины — L=Fвх' , где Fвх — площадь входного сечения канала; для угловой скорости — a./L.
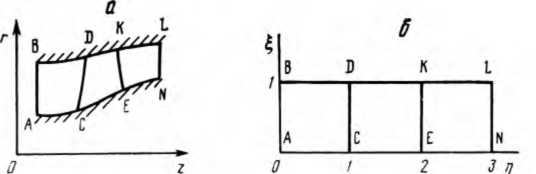
Рис. 1

Рис. 2
В расчетной области строилась однородная сетка, образованная пересечением линии ξ=const, η=const. УФТ аппроксимировалось на центрально-разностном девятиточечном шаблоне со вторым порядком точности. Решение системы конечно-разностных уравнений для находилось в результате итераций явным методом переменных направлений [9]. Подробнее ознакомиться с аппроксимацией ФТ можно в [11]. По известному на данной итерации полю Ψ плотность в области безлопаточного канала находилась из уравнения Бернулли, а в области рабочего колеса (РК) из условия постоянства ротальпии вдоль линии тока в относительном движении. Плотность обычно пересчитывалась через несколько итераций по Ψ.

Рис. 4
В центробежном компрессоре из [14] входной участок цилиндрический, а выходной участок радиальный (см. рис. 4, а). В этом случае на входе в канал задавалась Vr=0 (dΨ/dz=0), а на выходе Vz=0 (dΨ/dr=0). Результаты расчета дозвукового течения в центробежном компрессоре из [14] (в виде постоянства чисел Маха в относительном движении) при Q—0,226, ω=0,233 и однородных распределениях I0, S и Г=0 на входе (режим 2) приведены на рис. 4, а. На рис. 4, б для этого венца (с теми же Q и ω) приведены линии постоянства чисел Маха в относительном движении, рассчитанные при неоднородном распределении энтропии на входе в канал: S=0,05·Ψ+1η(1/κ)—0,025 (и — показатель адиабаты). Константы в распределении S от Ψ выбраны так, чтобы средняя по расходу величина энтропии на входе в канал была равна величине энтропии, соответствующей режиму 2. (Распределения I0 и Г на входе задавались, как и на режиме 2). Уменьшение энтропии в окрестности втулки приводит к увеличению уровня скоростей по сравнению с их уровнем на режиме 2 и, наоборот, увеличение энтропии в окрестности корпуса вызывает понижение уровня скоростей. Аналогичный характер влияния энтропии на течение в решетке профилей был отмечен в [15]. На рис. 5 показаны распределения давлений (Р=Р/Ра, Ра — атмосферное давление) на средней линии между соседними профилями на втулке этого венца, полученные в [14] экспериментально (штрих) и расчетом невязкого трехмерного течения (пунктир). Здесь же сплошной линией нанесены результаты расчета авторов на сетке (8X40 узлов). Время счета на ЭВМ ЕС-1061 составило 7 с.
Наблюдается удовлетворительное согласие расчетных данных, полученных разными методами.
Вывод.
Расчеты показали, что разработанная методика позволяет быстро и достаточно точно (в рамках принятой модели) рассчитывать течения в венцах осевых и центробежных компрессоров и может служить основой для создания эффективного алгоритма расчета течения в многоступенчатой турбомашине.
Авторы благодарят А. Н. Крайко за постановку задачи, М. Е. Дейча за полезные обсуждения результатов, В. Е. Макарова за помощь в работе.

