Приведенные выше системы уравнений термоэлектрических и термоэмиссионной КЭУ позволяют изучать их динамику на номинальном режиме методами аналогового моделирования. Целью такого изучения является определение степени устойчивости системы, а также оценка ее динамических свойств и статических отклонений интересующих исследователя координат под действием характерных возмущений.
В качестве характерных возмущений для термоэлектрической КЭУ можно принять: 1) изменение реактивности реактора; 2) изменение электрической нагрузки; 3) изменение расхода теплоносителя в контурах; 4) изменение условий сброса тепла холодильником-излучателем. Для термоэмиссионной КЭУ дополнительным возмущением может быть: 5) изменение давления паров щелочного металла в межэлектродном зазоре.
Для таких сложных систем, какими являются ядерные энергетические установки (ЯЭУ), не разработаны еще инженерные методы оценки их динамических свойств. Обычно такую оценку проводят качественно, по результатам моделирования, изучая переходные процессы, протекающие в системе после внесения возмущения. Для оценки динамических свойств системы следует учитывать следующие особенности переходных процессов: 1) характер распространения возмущения в системе; 2) степень колебательности переходного процесса или быстрота затухания колебаний; 3) величина максимальных отклонений параметров во время переходного процесса; 4) установившаяся величина отклонений параметров; 5) время протекания переходного процесса.
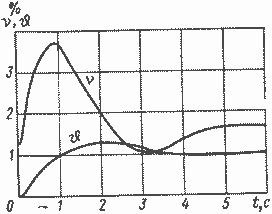
Рис. 4.4. Переходные процессы в КЭУ без системы регулирования
Имея в своем распоряжении результаты моделирования и учитывая перечисленные выше особенности переходных процессов, исследователь может сделать заключение о степени необходимости системы управления и сформулировать предъявляемые к ней требования.
Рассмотрим динамические свойства термоэлектрической КЭУ.
Типичный характер переходного процесса в установке при скачкообразном возмущении по реактивности приведен на рис. 4.4. Он носит слабоколебательный характер. Первый заброс, почти скачок, плотности нейтронов пропорционален внесенной реактивности, как это следует из уравнений (4.8) — (4.9):
![]()
где N0 — номинальное значение мощности реактора.
Далее характер переходного процесса определяется динамикой запаздывающих нейтронов, разогревом реактора и всей системы. Увеличение плотности нейтронов, следующее за начальным забросом, существенно зависит от величины и знака температурного коэффициента реактивности реактора d∆k/dTr в уравнении (4.9). Действительно, если рассмотреть упрощенную систему уравнений (4.1) — (4.9) при ϑвх=0; γ=0; l=0 и одну усредненную группу запаздывающих нейтронов, тогда из уравнений (4.2), (4.8) и (4.9) получим (при ξ=0; f=0) уравнение для плотности нейтронов (свободной составляющей):
![]()
(4.21)
где τ — постоянная времени для усредненной группы запаздывающих нейтронов;
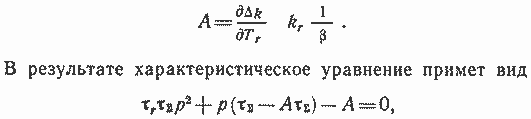
а корни характеристического уравнения
(4.22)

коэффициент демпфирования (при условии Л<0)
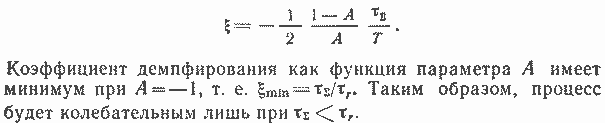
Необходимо отметить, что приведенный анализ крайне упрощен и позволяет установить лишь некоторые общие качественные характеристики процесса. Таким образом, при положительном температурном коэффициенте реактивности система будет неустойчивой, при отрицательном температурном коэффициенте реактивности система будет устойчива (см. рис. 4.4). При этом повышение температуры приводит к появлению отрицательной составляющей в Δk, которая при некотором росте температуры скомпенсирует внесенное возмущение. Конечное отклонение температуры будет равно
![]()
(4.23)
В соответствии с этой величиной будут и установившиеся отклонения других координат системы.
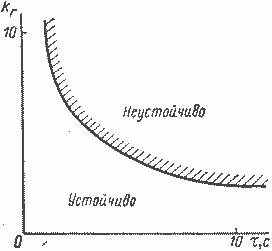
Рис. 4.5. Область устойчивости в функции температурного коэффициента реактивности
С точки зрения динамики системы желательно иметь достаточно большой отрицательный температурный коэффициент реактивности. При этом, как это следует из соотношения (4.23), отклонения температур будут достаточно малы и необходимости в системе управления может не возникнуть. Однако величина температурного коэффициента реактивности определяется конструктивными и технологическими особенностями реактора и не находится во власти проектировщика, так что реактор проектируется для выполнения определенной задачи, а температурный коэффициент является следствием получившейся конструкции и может быть даже положительным.
Исправление же нежелательных динамических и статических свойств установки, возникающих из-за получившегося слишком маленького температурного коэффициента реактивности реактора, возлагается на систему управления.
Следует заметить, что с увеличением отрицательного температурного коэффициента реактивности, начиная с его некоторых значений, увеличивается колебательность переходного процесса в системе. Более полное исследование, при котором учитываются влияние остальных координат на поведение системы, наличие нескольких групп запаздывающих нейтронов и мгновенных нейтронов, позволяет установить, что при определенном значении отрицательного температурного коэффициента реактивности система может потерять устойчивость. Поскольку минимальное значение коэффициента демпфирования для рассмотренной упрощенной модели зависит от тепловой постоянной времени реактора, область допустимых значений отрицательного температурного коэффициента реактивности также, очевидно, зависит от этой постоянной времени.
На рис. 4.5 показана область устойчивости КЭУ в функции температурного коэффициента реактивности и тепловой постоянной времени реактора. Диапазон предельных величин температурного коэффициента реактивности kr=(d∆k/dT) составляет примерно 10-3—10-2.
Переходные процессы в установке при других возмущениях носят в общем аналогичный характер, однако влияние возмущений, особенно возмущений по электрической нагрузке и по условиям излучения, будет меньше, как и соответствующие отклонения координат системы. Кроме того, области приложения этих возмущений находятся далеко от реактора, что приводит к более плавному протеканию переходных процессов.
В термоэмиссионной КЭУ, как отмечалось выше, тепловая инерционность реактора значительно больше, чем в термоэлектрических КЭУ. В соответствии с этим увеличивается и общее время переходных процессов при воздействии характерных возмущений. Поскольку для реакторов термоэмиссионных установок велико отношение τr/τ∑, область допустимых значений для отрицательного температурного коэффициента оказывается меньше.
Устойчивость термоэмиссионной КЭУ как объекта управления определяется устойчивостью реактора, который является единственным активным элементом в системе. В свою очередь устойчивость реактора зависит от характера температурных воздействий на реактивность, зависящих от параметров реактора и его элементов. По имеющимся в литературе сведениям, например, работа [6], значительное число конструкций реакторов с термоэмиссионными преобразователями не обладают достаточным отрицательным температурным эффектом. Одной из причин этому в ряде конструкций является выполнение тепловыделяющего элемента из нескольких блоков, разделенных зазором. При этом расширение блоков, вызываемое увеличением температуры, чем в основном и создается отрицательный температурный эффект, не приводит к существенному изменению реактивности реактора. Для высокообогащенного топлива незначительным оказывается и допплеровский эффект. В силу таких свойств реакторов последние будут обладать незначительным самовыравниванием, а для некоторых реакторов (при наличии в них положительного температурного коэффициента реактивности) КЭУ как объект управления может оказаться неустойчивой. С целью улучшения динамических свойств КЭУ с термоэмиссионным преобразованием энергии желательно такое изменение конструкции реактора, при котором он обладал бы отрицательным температурным коэффициентом реактивности. В частности, можно использовать с этой целью керамические тепловыделяющие элементы из вольфрамокиси урана [76].
При анализе динамических характеристик термоэмиссионных КЭУ следует учитывать влияние тракта подачи паров щелочного металла, нейтрализующих пространственный заряд и уменьшающих работу выхода электронов (цезий, рений и др.). С изменением давления паров в межэлектродном зазоре резко меняются характеристики преобразователя, режим его работы и выходное напряжение, что сказывается на динамических характеристиках КЭУ. Так, увеличение давления паров в определенном диапазоне приводит к увеличению плотности тока при постоянной температуре эмиттера [39].
С увеличением плотности тока соответственно увеличивается количество тепла, переносимое электронами с эмиттера, а следовательно, улучшается охлаждение эмиттера и уменьшается его тепловая инерционность.
Динамические характеристики таких элементов как холодильник-излучатель, трубопроводы, насосы, отражатель и замедлитель в реакторе, а также динамика нейтронных процессов являются общими для энергетических установок с различными способами преобразования тепловой энергии в электрическую и оказывают сходное влияние на динамику КЭУ в целом.
Выше отмечалось, что изучение динамических характеристик КЭУ с использованием сосредоточенной модели должно быть дополнено результатами более точного исследования на базе распределенной модели.
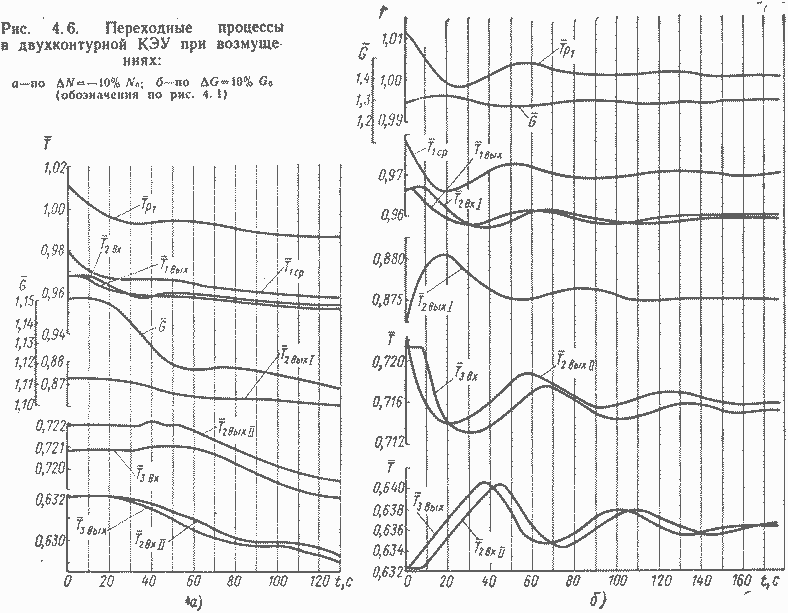
Для примера на рис. 4.6 приведены результаты расчетов переходных процессов в двухконтурной установке термоэлектрического типа, вызванных изменением мощности и расхода теплоносителя. Эти расчеты проведены по математической модели установки, составленной из моделей отдельных элементов, приведенных в гл. III.
Процессы носят колебательный характер; длительность переходных процессов обычно значительная, так как она определяется тепловой инерционностью как первого, так и второго контуров.
Характер переходных процессов в КЭУ в значительной степени определяется характером обратной связи по реактивности реактора, имеющей место в конкретной установке. В общем случае
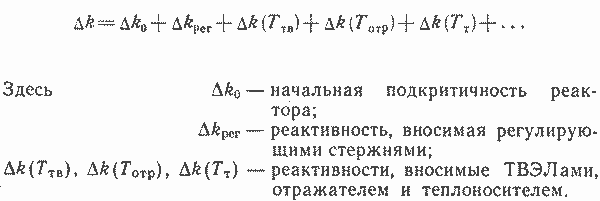
В зависимости от конструкции КЭУ на реактивность могут влиять и другие факторы, например: изгиб ТВЭЛов, а следовательно, перепад давлений на реакторе, изменение перепада температур на реакторе и пр.
Влияние на качество переходных процессов характера обратной связи по реактивности для двухконтурной КЭУ термоэлектрического типа видно из рассмотрения табл. 4.1.
Таблица 4.1.

Как показывают расчеты, космические ЭУ имеют диапазон линейности, определяемый отклонениями параметров ΔN±50%; ΔG=±10—20%. Для такого диапазона имеет смысл рассмотреть частотные характеристики установки. На рис. 4.7 приведены частотные характеристики двухконтурного КЭУ термоэлектрического типа, определяемые гармоническим изменением мощности на номинальном режиме работы с амплитудой, равной 12% N0. Частота воздействия изменялась в диапазоне ω=0-0,5 1/с. Из анализа частотных характеристик следует, что процессы в КЭУ можно разделить на две составляющие: быстрые процессы (в рассматриваемой конструкции это диапазон частот ω=0,05-0,5 1/с) и медленные (диапазон частот ω=0-0,01 1/с).
Быстрые процессы определяются изменением расхода теплоносителя и характеризуются малыми коэффициентами усиления, медленные — тепловыми процессами в установке. Частота пропускания первого (реакторного) контура в 2—3 раза больше частоты пропускания второго (излучательного) контура. Процессы в первом контуре характеризуются большим диапазоном линейности, чем процессы во втором контуре.
4.4. ЗАКОНЫ УПРАВЛЕНИЯ УСТАНОВКОЙ НА НОМИНАЛЬНОМ РЕЖИМЕ
Под законом управления понимают функциональную связь между измеряемыми координатами и управляющими воздействиями.
Измеряемые координаты.
В энергетических установках существует весьма обширный спектр измеряемых координат. В реакторе можно измерить плотность нейтронов или нейтронного потока, определяющую тепловую мощность реактора; различные температуры: теплоносителя на входе в реактор и на выходе из него, тепловыделяющих элементов, конструкций активной зоны и т. п.; расход теплоносителя через реактор, а также изменения температур в различных точках контуров установки. Можно и практически легко измерить электрические параметры — напряжение и силу тока термогенератора.
Управляющие воздействия.
Набор управляющих воздействий гораздо уже. Реактивность реактора можно изменять различными способами: с помощью размещенных в активной зоне или отражателе стержней или барабанов из материалов поглощающих, размножающих или замедляющих нейтроны; с помощью перемещения различных частей отражателя; с помощью частичного изменения геометрии реактора и т. п. В установках с термоэлектрическим преобразованием энергии можно изменять силу тока термогенератора путем воздействия на нагрузку. В простейших КЭУ малой мощности возможности управляющих воздействий этим и ограничиваются.
В более сложных установках [30] можно изменять величину расхода теплоносителя, в турбогенераторных КЭУ можно влиять на частоту и возбуждение генератора и т. д.
Требования к системе управления
Задачей управления на номинальном режиме работы установки является стабилизация режима и парирование возмущений. При этом можно сформулировать ряд требований, которым должна удовлетворять система автоматического управления (САУ).
- Точность поддержания режима.
В космических энергетических установках, как правило, требуется большая точность поддержания режима, чем в промышленных, транспортных и даже авиационных установках. Это требование вытекает из того, что крайнее ограничение массы заставляет конструкторов максимально форсировать режим работы. Поэтому допуски на регулирование получаются весьма малыми. Так, например, рабочая температура в американском атомном ракетном двигателе «Нерва» свыше 2500 К, в то время как температура плавления графита, из которого сделаны ТВЭЛы реактора, около 3300 К. Точность поддержания температуры в таком двигателе должна составлять около 50° или около 2%. Такие же жесткие требования к точности поддержания режима будут и в космических энергетических установках.
2. Динамическая точность.
Те же соображения, которые определяют необходимость высокой точности поддержания номинального режима, сужают и рамки допусков на динамические отклонения в процессе управления.
- Ограничение времени переходного процесса.
Поскольку динамические отклонения могут быть больше установившихся, к системе управления предъявляется требование минимизации времени переходных процессов.
- Надежность. Огромная стоимость космических экспериментов требует максимальной, по существу, абсолютной надежности аппаратуры, в том числе и аппаратуры системы управления.
- Кроме перечисленных (основных) требований, можно отметить требования, которые предъявляются к системам управления подобными объектами вообще, а именно: по возможности малые масса и стоимость, и небольшие габариты.
Осложняющим обстоятельством при конструировании системы управления космическими КЭУ являются тяжелые условия эксплуатации: высокая температура, радиация, космический вакуум.
В качестве главной особенности работы САУ космических ЭУ следует отметить невозможность или крайнюю затруднительность ремонта.
Перечисленные выше требования и особенности работы должны учитываться при выборе законов управления КЭУ и их сравнительной оценке.
Раздельное регулирование теплового и электрического контуров
К.п.д. установок с прямым преобразованием тепловой энергии в электрическую сравнительно низок и, как правило, не превышает 10—15% [72]. В таких установках рационально регулировать тепловой и электрический контуры с помощью независимых регуляторов/ В самом деле, даже очень большое воздействие на электрический контур установки (например, отключение нагрузки) из-за низкого к.п.д. не приведет к заметным изменениям в тепловом контуре· То есть управлять тепловым контуром, воздействуя на электрический, практически нельзя. Обратное влияние достаточно сильно, и в принципе можно управлять электрическим контуром, воздействуя, например, на тепловую мощность реактора. Однако в тепловом контуре установки всегда имеются свои задачи управления (ограничение температуры ТВЭЛов и др.), которые могут не согласовываться с потребностями управления электрическим контуром. К тому же инерционность электрических процессов значительно меньше инерционности тепловых процессов. Поэтому естественно разделение каналов управления тепловым и электрическим контурами установки. При этом каждый канал управления будет решать ограниченный круг задач, будет проще, а следовательно, и надежнее.
Для рассматриваемой упрощенной системы при k→∞ корни характеристического уравнения:
![]()
имеют отрицательную действительную часть, т. е. система устойчива при любых значениях k.
С другой стороны, при нейтронном законе управления не контролируется температура реактора, так как она связана с мощностью дифференциальной связью и зависит от других параметров системы (температуры теплоносителя на входе в реактор, расхода и пр.). Этот недостаток особенно существенен для высоконапряженных энергетических реакторов, которые работают в предельно допустимой области температур. Поэтому данный закон управления в чистом виде применяется в ненапряженных реакторах (экспериментально-физических и т. п.). В теплонапряженных же реакторах он применяется в сочетании с другими связями. Его функцией является улучшение динамических свойств системы управления. Кроме того, ионизационные камеры не являются достаточно надежным элементом системы управления. В случаях, когда от системы управления требуется повышенная надежность, как, например, в автономных космических ЭУ [6], применение их нежелательно.
Управление по температуре
В высоконапряженных энергетических установках стабилизация плотности нейтронов не обеспечивает заданного температурного режима их элементов. Температура элементов установки, помимо мощности реактора, зависит от расхода и температуры теплоносителя в контурах ЭУ [см. (4.1) — (4.8)]. Изменение условий излучения, расхода или теплофизических параметров материалов приводит при постоянном уровне мощности реактора к изменению температуры элементов. Так, например, при попадании КЭУ из затемненной области в освещенную солнцем, уменьшается количество тепла, сбрасываемого излучателем. Это приводит к повышению температуры излучателя и теплоносителя, а вслед за этим и к росту температуры других элементов КЭУ. В связи с этим естественно стремление ввести в закон управления сигнал по температуре, что существенно изменяет динамические свойства системы управления. Чтобы изучить характер такого воздействия, рассмотрим астатический закон управления с воздействием на реактивность только по температуре одного из элементов реактора (рис. 4.10). В качестве регулируемой координаты обычно используется температура теплоносителя на выходе из реактора, поскольку измерение температуры тепловыделяющих элементов технически трудно осуществимо.
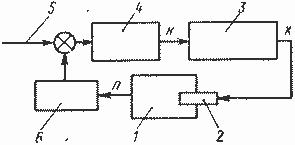
Рис. 4. 10. Структурная схема системы управления по температуре теплоносителя:
1 — реактор ЯЭУ; 2 — регулирующий орган; 3 — исполнительный двигатель; 4— усилитель; 5— задающее воздействие по уровню температуры; 6— термопара
Температура теплоносителя измеряется термопарой. Сигнал, пропорциональный отклонению температуры от заданного значения, усиливается и поступает на исполнительный механизм, который перемещает регулирующие органы реактора. Подобные системы регулирования разработаны, в частности, для космических КЭУ типа SNAP2; SNAP8, SNAP10A [89]. В операторной форме закон управления имеет вид

Здесь τ — постоянная времени привода;
τтп — постоянная времени термопары.
Характер переходных процессов в КЭУ зависит от ряда факторов: 1) величины мощностного и температурного коэффициентов реактивности; 2) тепловой инерционности реактора; 3) значений постоянных времени термопары и исполнительного механизма; 4) коэффициента усиления контура регулирования. Переходные процессы при таком законе управления имеют более колебательный характер и большую продолжительность, чем при стабилизации плотности нейтронов.
На рис. 4. 11 приведены переходные процессы при различных значениях мощностного коэффициента реактивности kN. С уменьшением этого коэффициента увеличиваются максимальные отклонения по мощности и регулируемой температуре, увеличиваются колебательность и длительность переходных процессов.
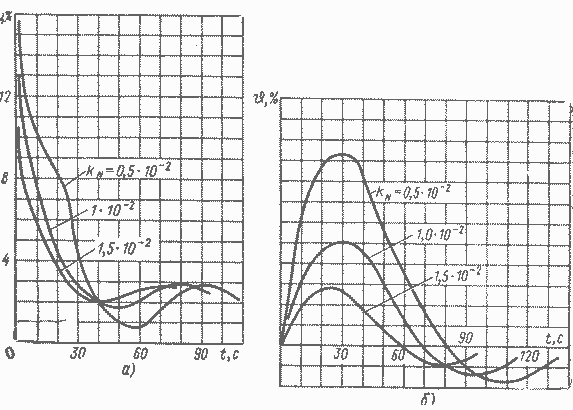
Рис. 4.11. Переходные процессы с регулятором температуры: а — по мощности; б — по температуре
С увеличением инерционности измеряемой температуры, термопары и привода качество переходных процессов ухудшается, увеличиваются отклонения по регулируемой координате, длительность переходных процессов и колебательность. Область допустимых значений коэффициентов усиления регулятора мала и очень зависит от динамических свойств элементов в контуре регулирования. С увеличением тепловой инерционности реактора между плотностью нейтронов и измеряемой температурой область допустимых коэффициентов усиления сокращается. При значительной тепловой инерционности реактора система может оказаться структурно неустойчивой, т. е. даже при очень маленьких коэффициентах усиления переходный процесс в системе будет расходящимся. В этом случае необходимо введение в закон управления стабилизирующих воздействий.
К достоинствам закона управления по температуре следует отнести, во-первых, обеспечение постоянного температурного режима элементов КЭУ и, во-вторых, надежность датчиков температуры (термопар). Недостатками этого закона управления являются: 1) плохие динамические свойства в сравнении с системой регулирования по плотности нейтронов (см. рис. 4.9 и 4.11); 2) невозможность установления больших коэффициентов усиления в контуре регулирования, поскольку с увеличением коэффициента усиления уменьшается запас устойчивости системы: 3) неприменимость его в энергетических установках с большой инерционностью, например в термоэмиссионных установках с встроенным в реактор преобразователем [66].

