7.3. ПУСКОВОЙ РЕЖИМ РЕАКТОРА С УЧЕТОМ ОГРАНИЧЕНИЙ И ТРЕБОВАНИЯ НЕЧУВСТВИТЕЛЬНОСТИ РЕЖИМА К ВОЗМУЩЕНИЯМ
В настоящем разделе изучается вопрос нахождения оптимальной программы пуска реактора при учете ограничений как по управлению, так и по периоду и скорости нарастания температуры реактора в общей постановке, как она дается в теории управления. Полученный оптимальный режим исследуется на его чувствительность к погрешностям реализации программы и выявляется, что слишком большая чувствительность оптимального режима пуска к возмущениям требует применения к вопросу программной оптимизации пускового режима подхода, отличного от обычного, используемого в теории управления. Этот подход и применяется для получения оптимальной программы пуска реактора.
7.3. 1. Исследование оптимального процесса пуска в общепринятой постановке задачи оптимизации
Рассмотрим процесс пуска реактора, включающий в себя вывод реактора из подкритического состояния в критическое, увеличение мощности реактора до уровня, обеспечивающего предельно допустимую скорость нарастания температуры реактора, и прогрев реактора до некоторой заданной температуры [68].
Будем учитывать следующие ограничения: 1) скорости перемещения регулирующего органа; 2) обратной величины периода реактора; 3) скорости нарастания температуры реактора. Последнее ограничение вводится, чтобы избежать внутренних термических напряжений в реакторе.
При этих ограничениях требуется найти программу изменения перемещения регулирующего органа, которая бы обеспечила наибыстрейший процесс пуска.
Принимаем, что реактор описывается уравнениями:

Как видно из приведенных уравнений, здесь учтена только усредненная группа запаздывающих нейтронов; в уравнении для плотности нейтронов член nl опущен, и тепловая часть реактора описана одной сосредоточенной массой. На этой упрощенной модели можно проследить основные закономерности, присущие режиму пуска при использовании предельных возможностей.
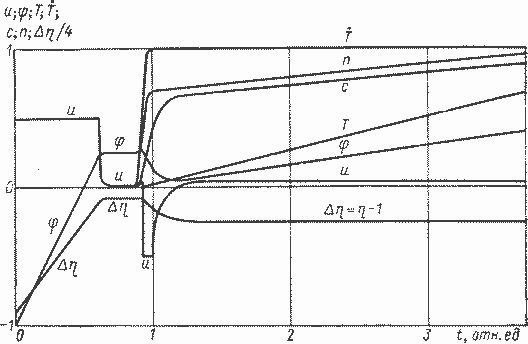
Рис. 7.8. Поведение основных величин, характеризующих процесс пуска реактора, в оптимальном режиме (без учета возмущений)
Учитывая оговоренные ограничения, можем сказать, что в течение процесса пуска должны выполняться неравенства
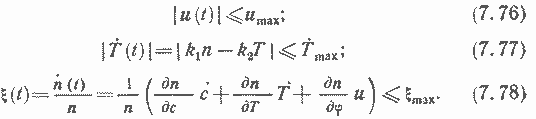
Начальные данные по переменным, для которых заданы дифференциальные уравнения, фиксированы. Задано также конечное значение температуры реактора.
Поставленная таким образом оптимальная задача пуска реактора является задачей теории оптимального управления с ограничением по управлению (7.76) и ограничениями на функцию фазовых координат [см. (7.12) и (7.77)] и на функцию фазовых координат и управления [см. (7.13) и (7.78)].
На рис. 7.8 изображены фазовые координаты φ, с и Т, а также управление и и величины η, 1—η и Т для оптимального процесса, построенного при некоторых типичных значениях числовых параметров системы (7.71) — (7.75). Для этого процесса было проверено выполнение необходимого условия оптимальности.
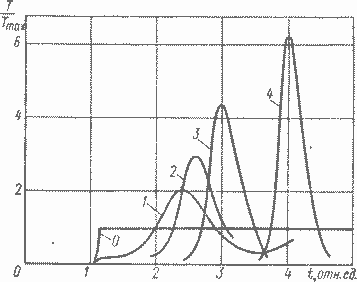
Рис. 7. 9. Изменение скорости нарастания температуры Т — при оптимальной программе и при различных отклонениях от оптимальной программы в сторону уменьшения реактивности
Отметим характерные особенности хода кривых оптимального процесса. Движение регулирующего органа φ имеет четыре основные участка: движение в положительном направлении с максимальной скоростью; движение с малой скоростью, соответствующее участку достижения периодом реактора своего предельного уровня; затем движение в отрицательном направлении с максимальной по абсолютной величине скоростью; плавный переход от движения с отрицательной скоростью к движению в положительном направлении с небольшой скоростью; движение с практически постоянной положительной скоростью регулирующего органа. Существенным является наличие участка движения регулирующего органа в отрицательном направлении. Этот участок является подготовкой системы к выходу на ограничение по скорости нарастания температуры реактора. Если подходить к этому ограничению без этого участка торможения, то даже при очень низких значениях скорости перемещения регулирующего органа получается недопустимо большой заброс скорости нарастания температуры реактора Т.
Исследования поведения системы при отклонениях от выбранной программы показывают, что незначительные отклонения от оптимальной приводят к большим превышениям допустимого уровня скорости нарастания температуры. На рис. 7.9 показано в относительных величинах поведение скорости изменения температуры реактора при идеальном осуществлении оптимальной программы (кривая 0) и при отклонениях закона перемещения регулирующего органа от оптимального (остальные кривые). При этом рассматривались возмущенные программы перемещения регулирующего органа φ(t), которые получаются из оптимальной программы φ°(t) смещением вдоль оси φ на некоторую постоянную величину Δφ. Кривые 1, 2, 3, 4 соответствуют смещениям программы в отрицательную сторону, т. е. в сторону уменьшения вклада в реактивность от регулирующего органа. При оптимальной программе ограничение по скорости нарастания температуры Т удовлетворяется. Поэтому можно было ожидать, что в рассмотренном возмущенном движении, в котором вклад в реактивность регулирующего органа никогда не больше, чем в оптимальном процессе, значения скорости нарастания температуры Т во все моменты времени будут не выше, чем в оптимальном случае, т. е. также не будут превышать установленного ограничения.
Однако из рис. 7.9 видно, что это не так и что величина Т превосходит в этих возмущенных движениях свое допустимое предельное значение, и притом весьма существенно. Правда, на начальном участке, на котором в оптимальном случае уже достигнуто ограничение по Т, кривая T(t) для возмущенного движения идет значительно ниже соответствующей кривой для оптимального движения. Однако далее следует участок, на котором кривая достигает и значительно превосходит предельное допустимое значение Ттах.
Этот факт имеет следующее объяснение. В процессе пуска реактор выводится из начального состояния, характеризующегося некоторой подкритичностью и низким уровнем нейтронной мощности, определяемой источником нейтронов. Основная часть диапазона нейтронной мощности, составляющая несколько порядков, проходится при положительном значении реактивности ∆k. Как видно из выражения (7.74), уровень нейтронной мощности в каждый определенный момент времени определяется уровнем концентрации ядер-предшественников запаздывающих нейтронов с и значением реактивности Δk. Из уравнений (7.72, 7.74) также видно, что плотность ядер-предшественников запаздывающих нейтронов может нарастать лишь при положительных значениях реактивности Δk (при уровнях концентрации ядер-предшественников запаздывающих нейтронов, позволяющих пренебречь влиянием источника нейтронов S).
Для того чтобы была достигнута скорость нарастания температуры Тmах, уровень нейтронной мощности должен быть доведен до определенного значения, определяемого теплоемкостями прогреваемых масс. Во избежание же заброса Т необходимо, чтобы к моменту времени t2 (достижения величиной Т уровня Тmах) производная по времени нейтронной мощности была близка к нулю.
Производная же по времени нейтронной мощности определяется соответственно производными концентрации запаздывающих нейтронов и реактивности. Поскольку в пусковом режиме подход к «мощности разогрева» (так назовем условно мощность, при которой происходит разогрев СО скоростью Тmах) происходит снизу, то возможны два варианта состояния кинетики, при которых выполнены указанные выше требования к уровню и производной нейтронной мощности. Первый вариант состоит в том, что уровень концентрации ядер-предшественников запаздывающих нейтронов близок к уровню, соответствующему мощности разогрева, определяемому соотношениями с и η в критическом состоянии. При этом реактивность ∆k должна быть близка к нулю. Второй вариант состояния кинетики состоит в том, что концентрация ядер-предшественников запаздывающих нейтронов ниже уровня, соответствующего мощности разогрева при том соотношении между нейтронной мощностью и концентрацией предшественников запаздывающих нейтронов, которое имеет место при критическом состоянии реактора. При этом реактивность имеет положительное значение, существенно отличающееся от нуля.
В оптимальном режиме при выходе на ограничение по Т реализуется именно второй вариант состояния кинетики. В момент времени достижения скоростью нарастания температуры предельного уровня Tmах имеется значительная положительная реактивность и концентрация ядер-предшественников запаздывающих нейтронов отстает от уровня, соответствующего мощности разогрева при соотношении, отвечающем критическому состоянию реактора. После точки, в которой Т достигает уровня Tmах в оптимальной программе (которая, будучи выбрана однажды, остается неизменной), регулирующий орган продолжает перемещаться в сторону уменьшения реактивности на некотором промежутке времени, к концу которого реактивность сводится практически к нулю, а концентрация ядер-предшественников запаздывающих нейтронов достигает уровня разогрева. Лишь после этого регулирующий орган начинает перемещаться в сторону увеличения реактивности, компенсируя отрицательное воздействие температуры на реактивность.
При возмущенном движении, когда кривая перемещения регулирующего органа проходит на некотором участке времени ниже кривой, соответствующей оптимальному режиму, участок, на котором реактивность положительна, становится короче по сравнению с таким же участком в оптимальной программе, и значения положительной реактивности на этом участке становятся меньше. Соответственно на этом участке концентрация ядер- предшественников запаздывающих нейтронов и нейтронная мощность не успевают достичь уровня разогрева, и дальнейшее их нарастание происходит уже на участке программы, на котором регулирующий орган начинает перемещение в сторону увеличения реактивности с небольшой скоростью. В рассматриваемом возмущенном движении нарастание концентрации ядер-предшественников запаздывающих нейтронов происходит менее форсированно по сравнению с оптимальным случаем, и поэтому к моменту достижения величиной Т своего предельного значения Тмах (а нейтронной мощностью — уровня разогрева) значение концентрации ядер-предшественников запаздывающих нейтронов получается близким к значению, соответствующему мощности разогрева при критическом состоянии реактора. Но реактивность к моменту достижения ограничения по t имеет положительное значение. Кроме того, после этого момента времени регулирующий орган продолжает перемещаться в сторону увеличения реактивности, что приводит к дальнейшему нарастанию нейтронной мощности и вызывает большой заброс по ограничиваемой в системе координате Т.
Таким образом, мы установили, что отклонение программы изменения положения регулирующего органа даже в сторону уменьшения реактивности приводит к большим забросам по ограничиваемой величине — по скорости нарастания температуры Т.
На рис. 7.10 показано относительное превышение ограничения по Т

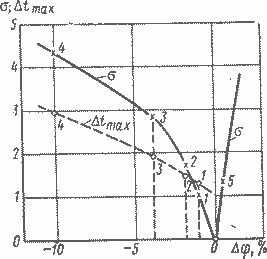
Рис. 7. 10 Зависимость относительного превышения ограничения по скорости нарастания температуры и смещения точки максимума T(t) в функции отклонения программы перемещения регулирующего органа от оптимальной
Как видно из кривых рис. 7.9, процесс, возникающий при пуске с неточно реализованной оптимальной программой, имеет явно выраженный колебательный характер, тогда как в оптимальном процессе пуска колебательность системы никак не сказывается· Можно сказать, что колебательные свойства объекта в оптимальной программе, скомпенсированы выбором поведения регулирующего органа. В возмущенном движении эта колебательность отчетливо выявляется.
Проведенное исследование показывает, что рассматривавшаяся программа пуска реактора, будучи оптимальной при идеальном подходе к задаче, в действительности оказывается непригодной для практического использования, если учесть зависимость режима от возмущений.
7. 3. 2. Задача оптимального пуска реактора с учетом требования конечной устойчивости и алгоритм ее приближенного решения
В связи с выявленной выше критичностью оптимального режима пуска реактора при «классическом» подходе к задаче оптимизации возникает мысль, что задачу отыскания оптимальной программы пуска следует формулировать с учетом нежелательных воздействий на систему. Сформулируем эту задачу в следующем виде [68].
Будем считать, что реактор в период пуска описывается уравнениями:
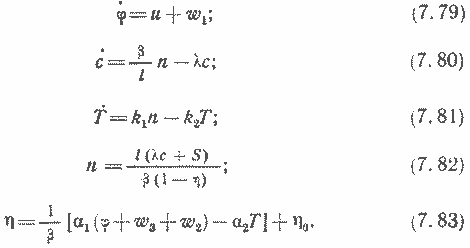
Здесь w1, w2 и w3 — возмущающие факторы.
Необходимо найти программу изменения во времени скорости перемещения регулирующего органа [функцию u(t)], обеспечивающую пуск реактора за минимальное время, т. е. переход реактора из начального состояния в конечное, характеризующееся достижением температурой реактора определенного уровня Тк. При этом налагаются такие ограничения:
- скорость перемещения регулирующего органа не должна превышать предельного значения umax;

Из приведенной постановки задачи с учетом требования конечной устойчивости классическая постановка задачи оптимального пуска получается, если положить Δ1, Δ2 и Δ3 равными нулю.
Введенные возмущающие воздействия представляют собой воздействия по реактивности [см. (7.83)]. При этом возмущения по реактивности допускаются скачкообразные (w3(t)], плавные [w1(t)], и в виде постоянных смещений по реактивности (w2).
Требование, сформулированное в п. 2 новой постановки задачи оптимального пуска реактора, мы будем называть требованием конечной устойчивости режима. Словом «конечная» при этом подчеркивается то, что допускаются отклонения возмущений лишь в фиксированных (конечных) пределах. По отношению именно к этим возмущениям требуется, чтобы возмущенный процесс не выходил за допустимые пределы.
Такой постановкой задачи учитываются неточности положения регулирующего органа, несоответствие начального состояния расчетному, изменение условий теплообмена с внешней средой и другие воздействия.
Здесь все возмущения отнесены к эквивалентному изменению реактивности. Можно, разумеется, вводить всевозможные другие возмущения и по отношению к ним формулировать требование конечной устойчивости оптимального режима.
Задача оптимального пуска при наличии требования конечной устойчивости является обобщением оптимальной задачи с ограничением на фазовые координаты: требование, чтобы координатами системы удовлетворялись некоторые неравенства [см. (7.77), (7.78)] заменяется при этом более сильным требованием конечной устойчивости режима.
Оптимальное управляющее воздействие u(t) при учете требования конечной устойчивости должно выбираться в каждый момент времени так, чтобы наихудшее из возможных поведений возмущающих воздействий w2(t), не могли вывести систему при данном значении t из допустимых пределов. К тому же надо выбирать функцию u(t) так, чтобы весь процесс длился как можно короче.
Из сказанного следует, что для каждого момента времени должны решаться следующие две оптимальные задачи.
Задача 1. При известном законе изменения управляющего воздействия u(t) в интервале времени от 0 до t найти такие функции w1(τ), w2(τ), w3(τ), которые, удовлетворяя ограничениям (7.84) — (7.86), дают при τ=1 максимальное значение обратной величины периода реактора.
Задача 2. При известном законе изменения управляющего воздействия u(τ) в интервале времени от 0 до t найти такие функции w1(τ), w2(τ), w3(τ), которые, удовлетворяя ограничениям (7.84) — (7.86), дают в момент времени τ = ί максимальное значение скорости нарастания температуры реактора Т.
Найденные решением задач 1 и 2 максимальные значения ξ и Т, соответствующие определенно выбранному t, должны не превышать установленных пределов. Подчеркнем, что в общем случае решать задачи 1 и 2 нужно для каждого t отдельно.
Управляющее воздействие — скорость перемещения регулирующего органа u(t) — должно выбираться с учетом этих максимальных отклонений по ξ и Т.
Ниже излагается приближенный алгоритм, позволяющий построить управляющее воздействие u(t) в сформулированной задаче оптимального пуска реактора с требованием конечной устойчивости. Этот алгоритм использует рассмотренные выше особенности возмущенных движений, вызванных отклонениями программы перемещения регулирующего органа от программы, оптимальной при классической постановке задачи оптимизации пуска. Алгоритм этот состоит в следующем.
Интегрируется система дифференциальных уравнений (7.79) — (7.83) при перемещении регулирующего органа в сторону увеличения реактивности с максимальной скоростью umax и поведении всех возмущающих воздействий w1(t), w1(t) и w3(t),
приводящем к максимально возможному увеличению реактивности, от начального состояния до момента времени t(1), при котором достигается ограничение по обратной величине периода реактора (см. рис. 7.12). Справа от этого момента времени t(1) находится такой закон изменения во времени скорости перемещения регулирующего органа, чтобы при действии всех возмущающих факторов в сторону увеличения реактивности обратная величина периода реактора была равна своему предельно допустимому значению ξmaх.

Для нахождения «наихудших» возмущений в задачах 1 и 2 можно использовать следующую приближенную методику. Поясним ее применительно к задаче 2. Для различных точек на кривой процесса исследуются уравнения линейного приближения для возмущающих движений. При замороженных коэффициентах находятся передаточные функции от возмущающих воздействий w1(τ) и w3(τ) к скорости нарастания температуры:

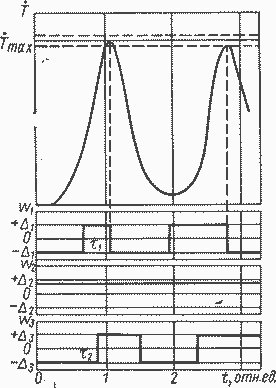
Рис. 7.11. Изменение ограничиваемой величины Т и возмущающих воздействий w, для случая управления с учетом требования конечной устойчивости
Аналогичный анализ проводится и для задачи 1. Оказывается, что наихудшие значения ξ получаются при действии всех возмущений в сторону увеличения реактивности. Такой эффект понятен, если принять во внимание, что выбросы при отклонении программы изменения реактивности в сторону ее уменьшения обусловлены наличием отрицательной обратной связи от температуры к реактивности.
На участке времени [t(1)— t(2)) — где достигается ограничение по ξ, температура еще не начала изменяться. Мало она изменяется и до точки t(3).
Ранее отмечалось, что при отклонениях программы перемещения регулирующего органа в сторону уменьшения реактивности, максимум по tвеличины Т смещается в сторону больших t, а сам максимум возрастает (см. рис. 7.9 и 7. 10). Этот факт используется для построения алгоритма отыскания программы изменения во времени скорости перемещения регулирующего органа для t>t(4). Весь диапазон изменения постоянного возмущения Wz разбивается на 2n участка.



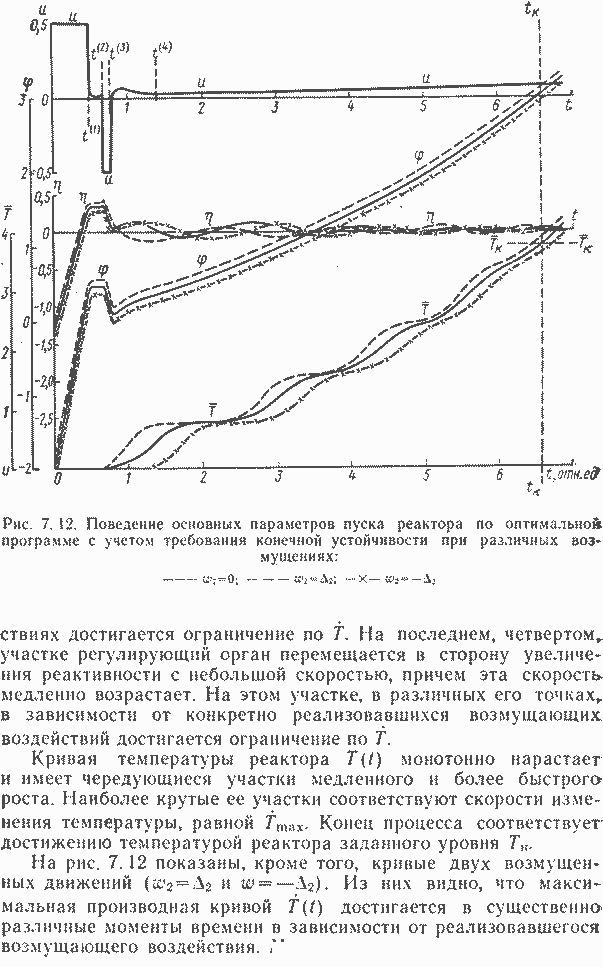
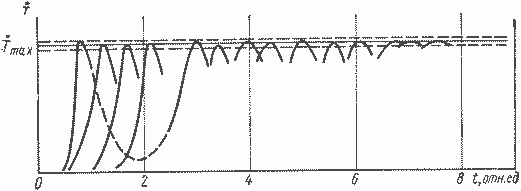
Рис. 7.13. Поведение Т при различных реализациях возмущающих воздействий (для случая оптимальной программы с учетом требования конечной устойчивости)
Момент достижения конечного значения температуры Тк сдвигается, а общий характер кривых получается одинаковым.
На рис. 7.13 показано, как подходит величина Т к своему предельному значению Ттах при различных реализациях возмущающих воздействий. Как видно, момент выхода на ограничения очень сильно зависит от конкретной реализации возмущающего воздействия. Однако процесс рассчитан так, что максимальные выбросы по Т при всех видах возмущающих воздействий (в пределах точности вычислений) равны Ттах. Тем, что эти забросы находятся на пределе, достигается максимально возможное быстродействие.
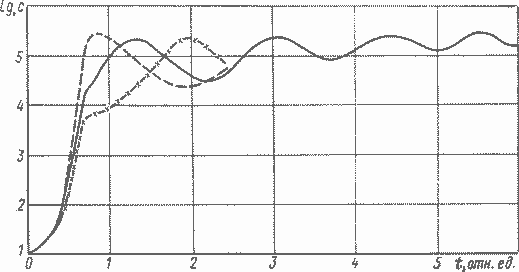
Рис. 7. 14. Поведение концентрации ядер-предшественников запаздывающих нейтронов при различных возмущающих воздействиях (для случая оптимальной программы с учетом требования конечной устойчивости) (обозначения по рис. 7. 12)
На рис. 7. 14 приводятся кривые c(t) концентрации ядер-предшественников запаздывающих нейтронов при различных реализациях возмущающих воздействий. Характерно, что эти кривые отличаются друг от друга на отдельных участках времени примерно на два порядка. И несмотря на это, при одной и той же программе перемещения регулирующего органа максимальные выбросы по Т не превосходят уровня Тmах и практически ему равны.
Таким образом, предложенный приближенный алгоритм нахождения оптимального управления в рассматриваемой задаче пуска с учетом требования конечной устойчивости позволяет ввести более точное описание реактора, чем уравнения (7.79) — (7.83). Расчет по изложенному алгоритму при более полном описании тепловой части реактора (тринадцатым порядком) и учете шести групп запаздывающих нейтронов дает [68] лишь небольшие количественные отклонения в режиме, никак не сказавшиеся на качественном характере решения. Учет всех групп запаздывающих нейтронов вносит более значительные количественные изменения в программу пуска, чем уточненное описание тепловой части установки.
* Под линейностью понимается пропорциональность отклонений параметров величине возмущающего фактора при неизменном качестве переходного процесса.

