Механические испытания гибких кабелей - Определение упругих характеристик кабеля при растяжении-кручении

Экспериментально-теоретическое определение упругих характеристик кабеля при растяжении-кручении
Достаточно подробно методы изучения прочностных и упругих свойств композитов изложены в работе [11]. Приведенные здесь методы применимы для определения свойств таких конструкций, как кабели и канаты. Нам, однако, предпочтительнее использовать метод, где было бы реализовано не только стесненное растяжение, но и свободное. Это связано с тем, что для задачи растяжения при тех условиях, которые были сформулированы в монографии [15], в качестве упругих характеристик были использованы Е1, v1, G, полностью определяющие свойства условного спирального элемента кабелей. Для их определения необходимо три неодинаковых опыта на: стесненное растяжение; стесненное кручение; свободное растяжение или на свободное кручение с реализацией моторного эффекта.
В работе [16] приводится усовершенствованная методика расчета силы натяжения грузонесущего кабеля для геофизических исследований. При этом главное внимание было уделено учету конструкционного износа брони. В работе [17] описан прибор для определения жесткости гибких кабелей. Здесь авторы предполагали использовать раскрутку кабеля (моторный эффект) при растяжении для оценки жесткости на кручение. Однако сразу же было исключено из учета удлинение при раскрутке. Возможности прибора позволяли это сделать, однако неотработанность методики по исчерпывающему анализу диаграмм нагрузка — разгрузка привела авторов к недооценке учета удлинения кабеля.
В работе [18] приводится методика расчета конструктивного сечения токопроводящей жилы с учетом геометрии составляющих элементов. Представляет интерес методика определения зависимости изменения электрического сопротивления жил от нагрузки и параллельного замера Р ~ ε.
В работах [19—21] систематически использовалась теория упругости для расчета конструкции растягивающих кабелей и для оценки их жесткости и напряженно-деформированного состояния кабелей.
Для оценки моторных эффектов был использован прибор для определения жесткости кабеля [17], с помощью которого можно определять и удлинение кабеля от продольной нагрузки. Однако наличие оптической системы делает процесс замера очень трудоемким и требует при нагружении четкого совпадения центра масс грузов с продольной осью кабеля.
Для измерения удлинения кабеля при осевом нагружении на базе прогибомера 6ПАО разработано устройство* (рис. 1.3), позволяющее определять деформацию кабеля с точностью до 0,01 мм.

*Разработал устройство и провел испытания В. Д. Шиянов.

Образец кабеля 1 в подвешенном состоянии закреплялся в неподвижном зажиме 2. К другому концу прикреплялась грузовая платформа 3, на которой размещались калиброванные грузы. Тросик 4, связанный одним концом с подшипниковым узлом 5, проходит через блоки прибора 6ПАО 6 и блок 7. Груз 8 обеспечивал необходимое натяжение тросика.
При продольном нагружении кабель раскручивался и удлинялся, перемещая блок приборов, связанный с регистрирующим устройством. Для случая без вращения кабеля грузовая платформа стопорилась в опорах 9 со свободным перемещением вниз.

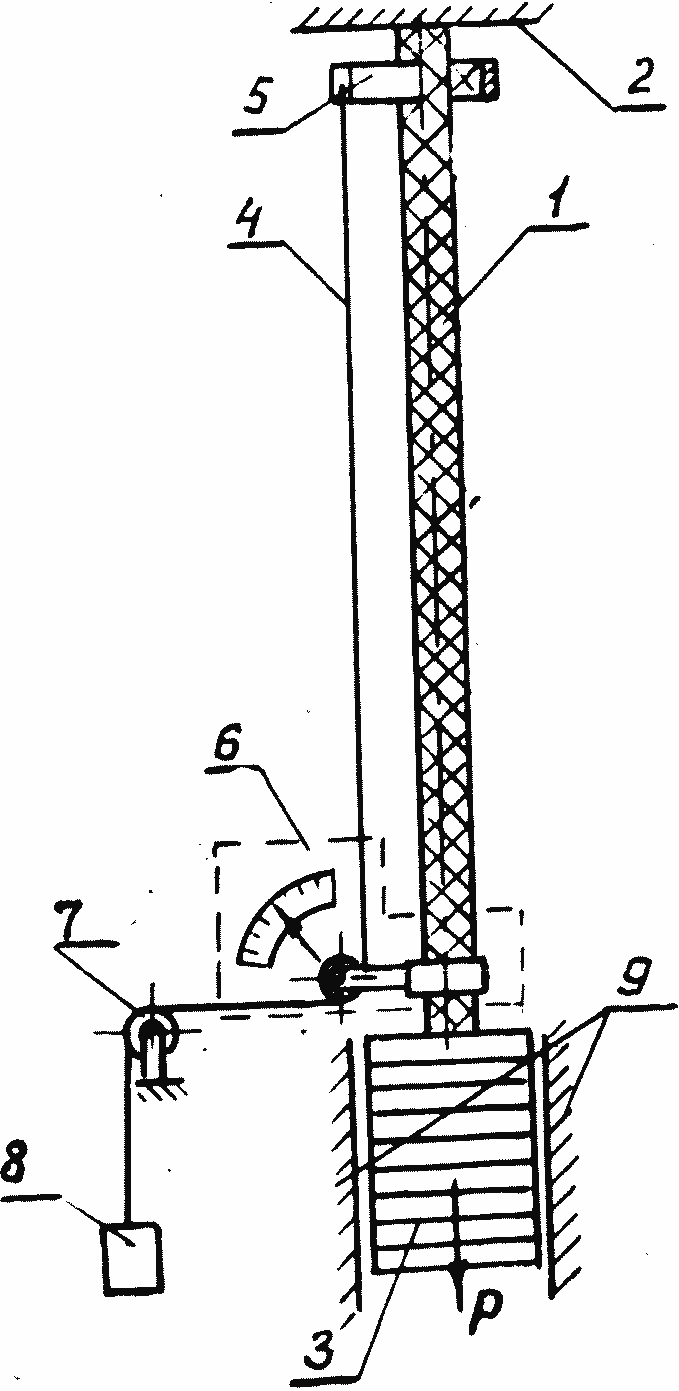
Рис. 1.3. Устройство для определения упругих характеристик кабеля при растяжении—кручении
Для измерения угла раскручивания тросик закреплялся на кабеле так, чтобы наматываться на него или калиброванную втулку, а сам прибор закрепляли вне кабеля. Измерялся угол раскручивания и регистрировалась зависимость нагрузка — угол поворота. Снятие показаний прибора производилось при циклах нагрузка—разгрузка в случаях свободного вращения кабеля и без раскручивания.
Результаты эксперимента представлены на рис. 1.4— 1.7. Из рисунков видно, что при свободном кручении (кривые /) относительное удлинение существенно больше, чем при стесненном растяжении (кривые 2). Для всех случаев кривые нагрузка—разгрузка гистерезисного типа.

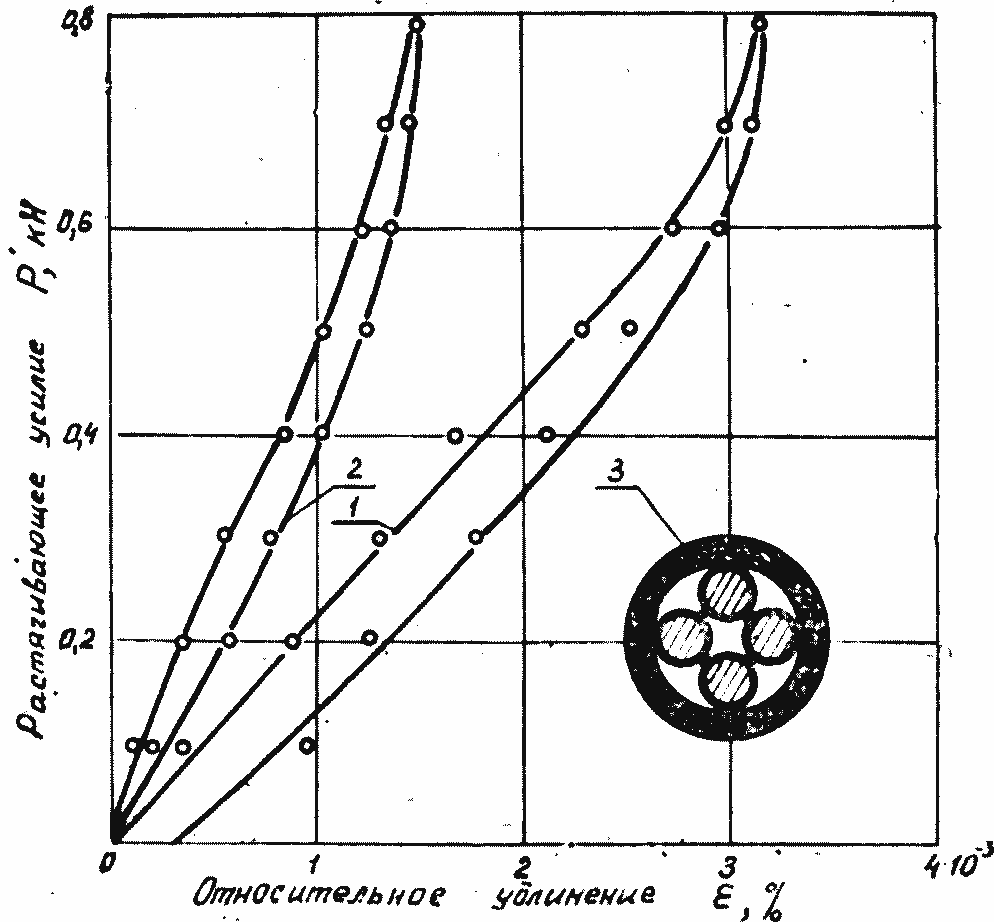
Рис. 1.4. Диаграмма Р~ε кабеля КРПТ: 1 — свободное растяжение — разгрузка; 2 — стесненное растяжение — разгрузке; 3 — поперечное сечение кабеля
В табл. 1.1 приведены значения отношении площадей петель гистерезисаи отношений работ при нагружении(i — порядковый номер исследуемого кабеля).
Для определения Е1, v1, G используем систему уравнений [15]:

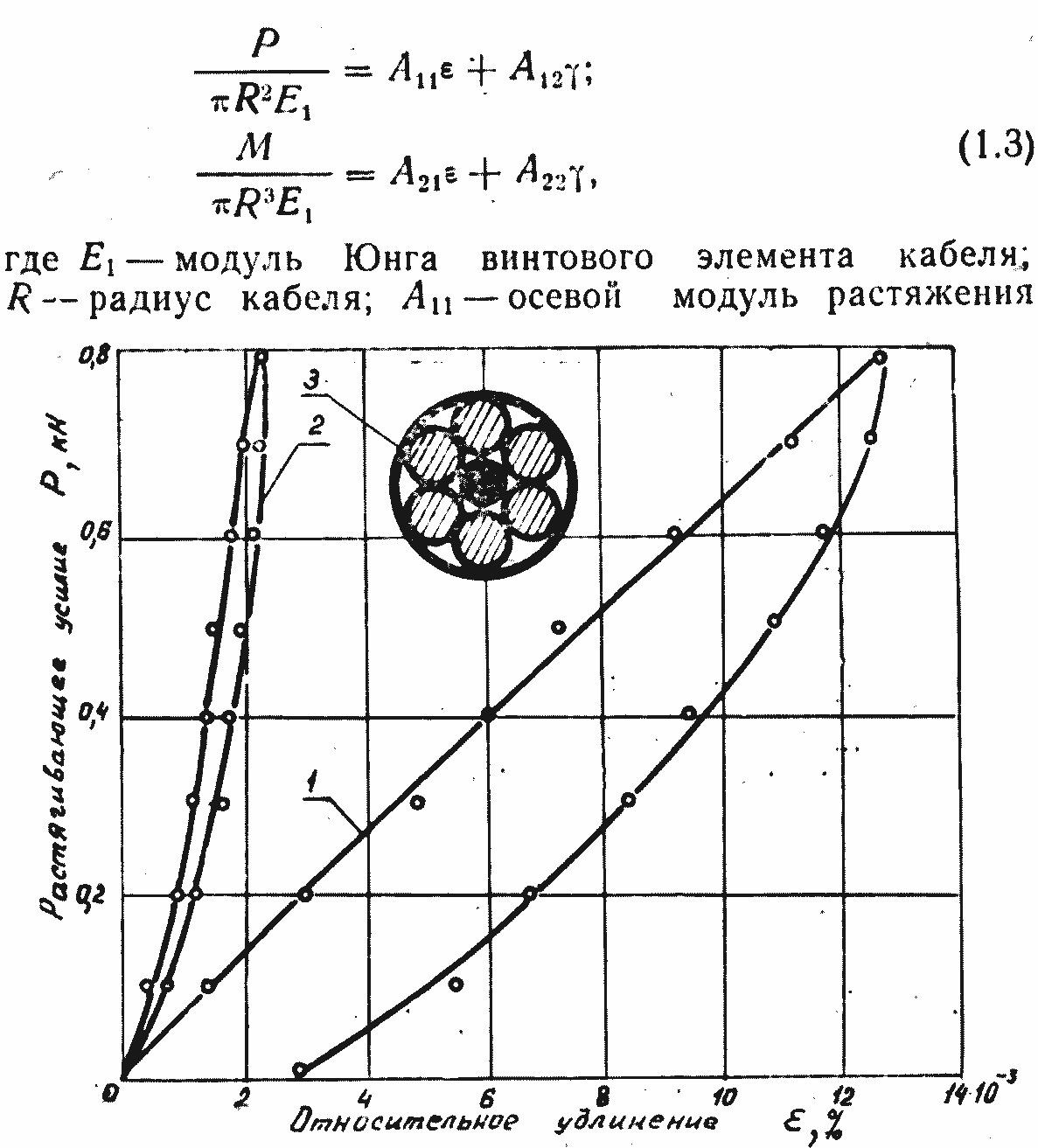
Рис. 1.5. Диаграмма Р~е кабеля КГШ: 1 — свободное растяжение- разгрузка; 2 — стесненное растяжение — разгрузка; 3 — поперечное сечение кабеля
Таблица 1.1

кабеля; А12=А21 — крутильно-растягивающий модуль (коэффициент влияния); А22 — модуль кручения; γ —  погонный угол закручивания.
Рассмотрим два варианта загружения, соответствующие приведенным графикам. Пусть растяжение реализуется в стесненных условиях, когда γ=0 (см. рис. 1.4—1.7, диаграмма 2).

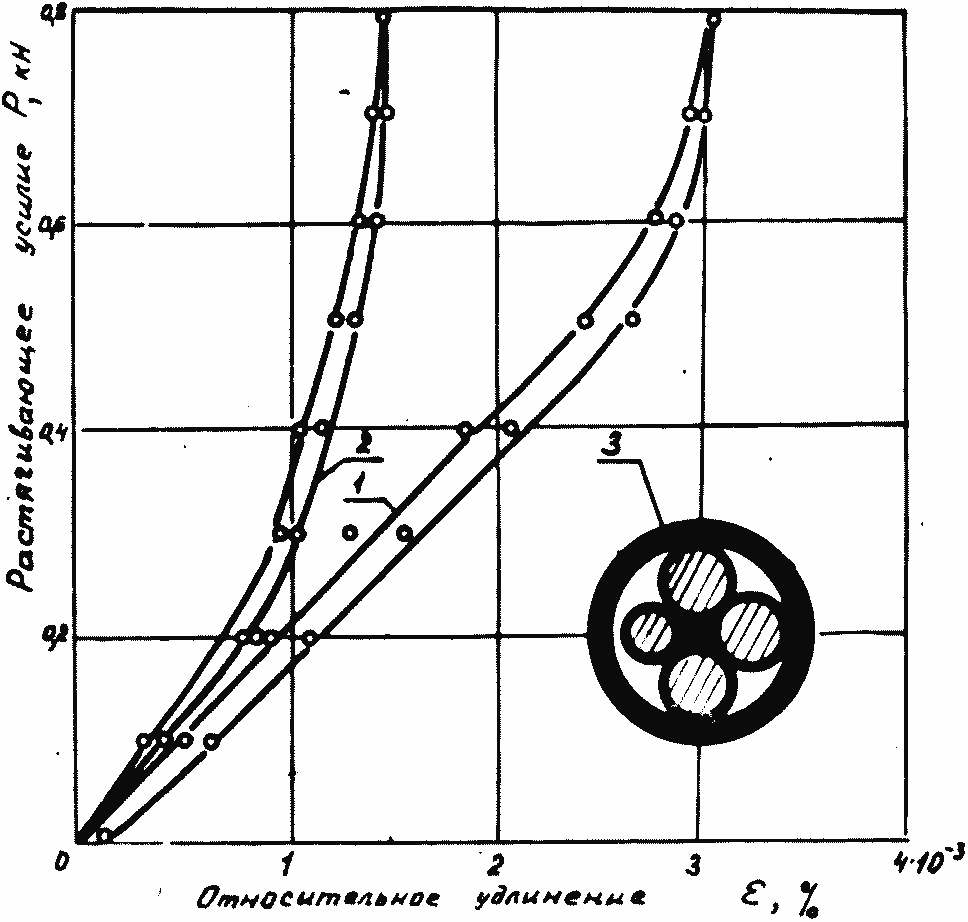
Рис. 1.6. Диаграмма Р~ε кабеля КРПС с круглым сердечником: 1 — свободное растяжение — разгрузка; 2 — стесненное растяжение — разгрузка; 3 — поперечное сечение кабеля
Тогда из (1.3) получаем (примем зависимости Р~ε линейными):


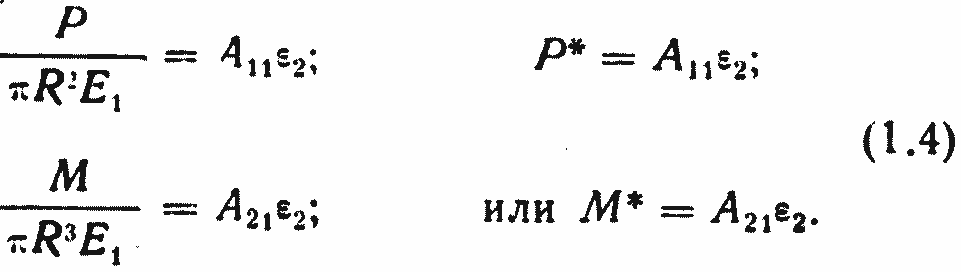
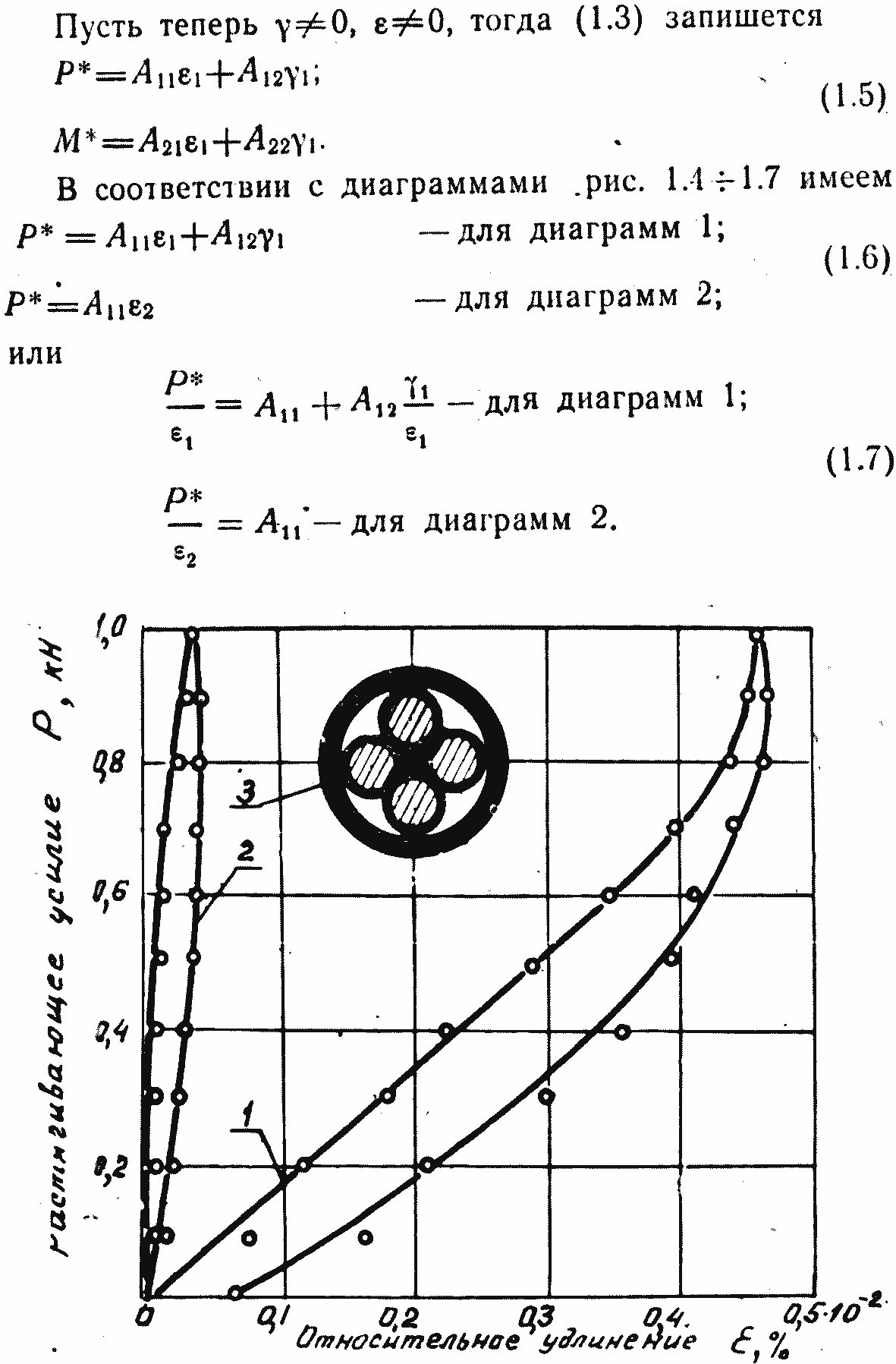
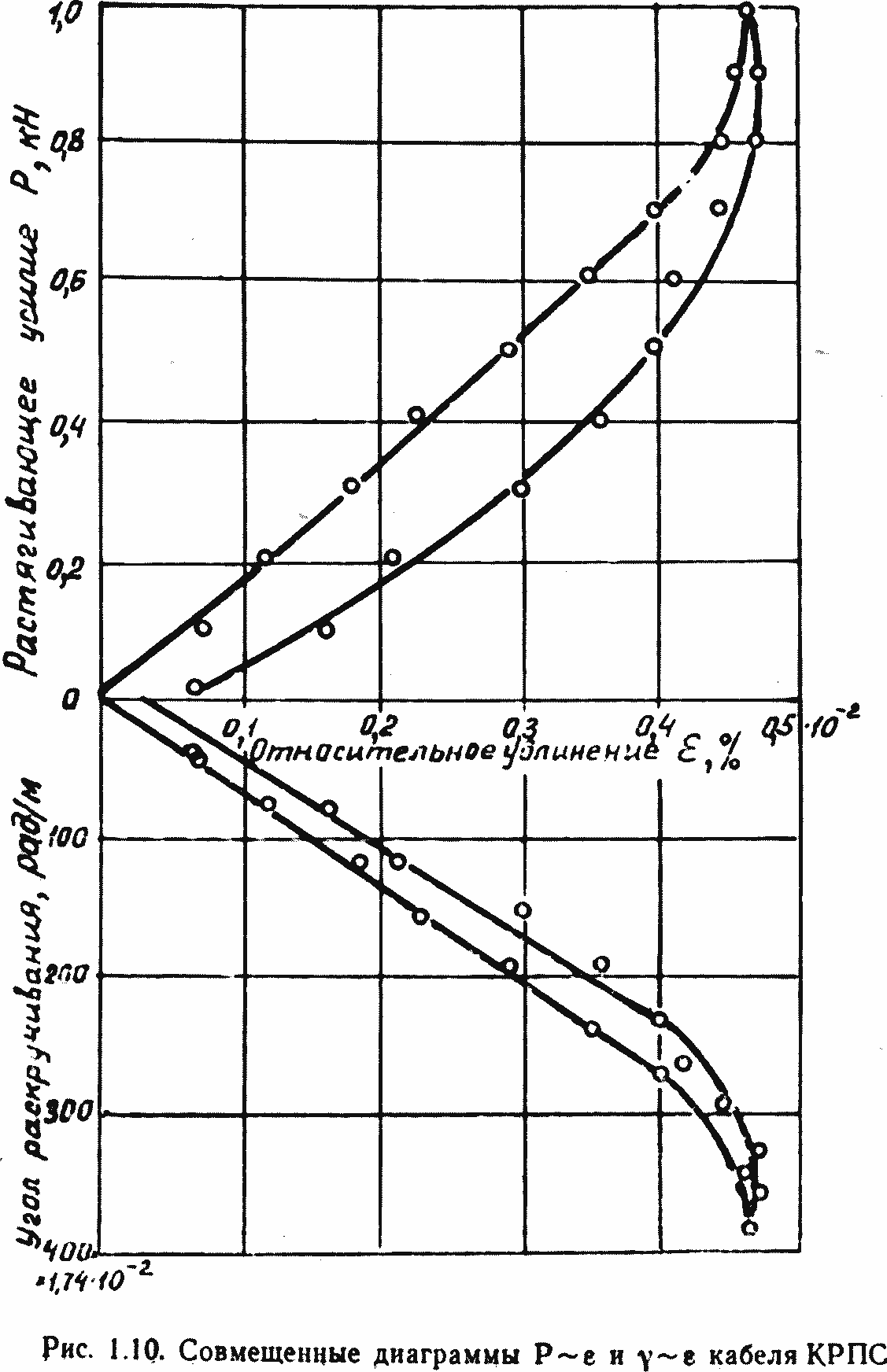
Рис. 1.7. Диаграмма Р~ε кабеля КРПС: 1 — свободное растяжение-разгрузка; 2 — стесненное растяжение — разгрузка; 3 — поперечное сечение кабеля

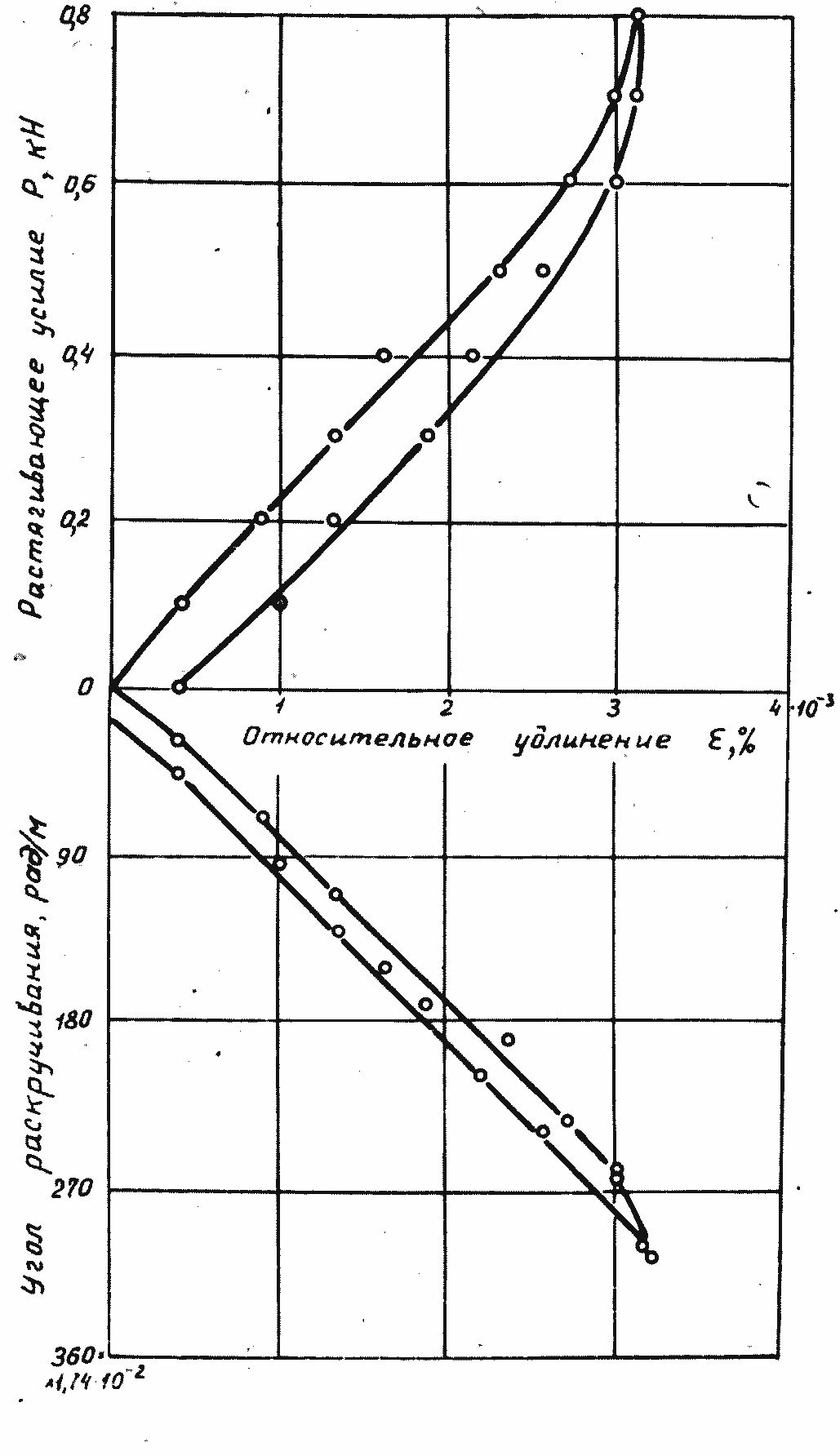
Рис. 1.8. Совмещенные диаграммы Р~ε и γ~ε кабеля КРПТ

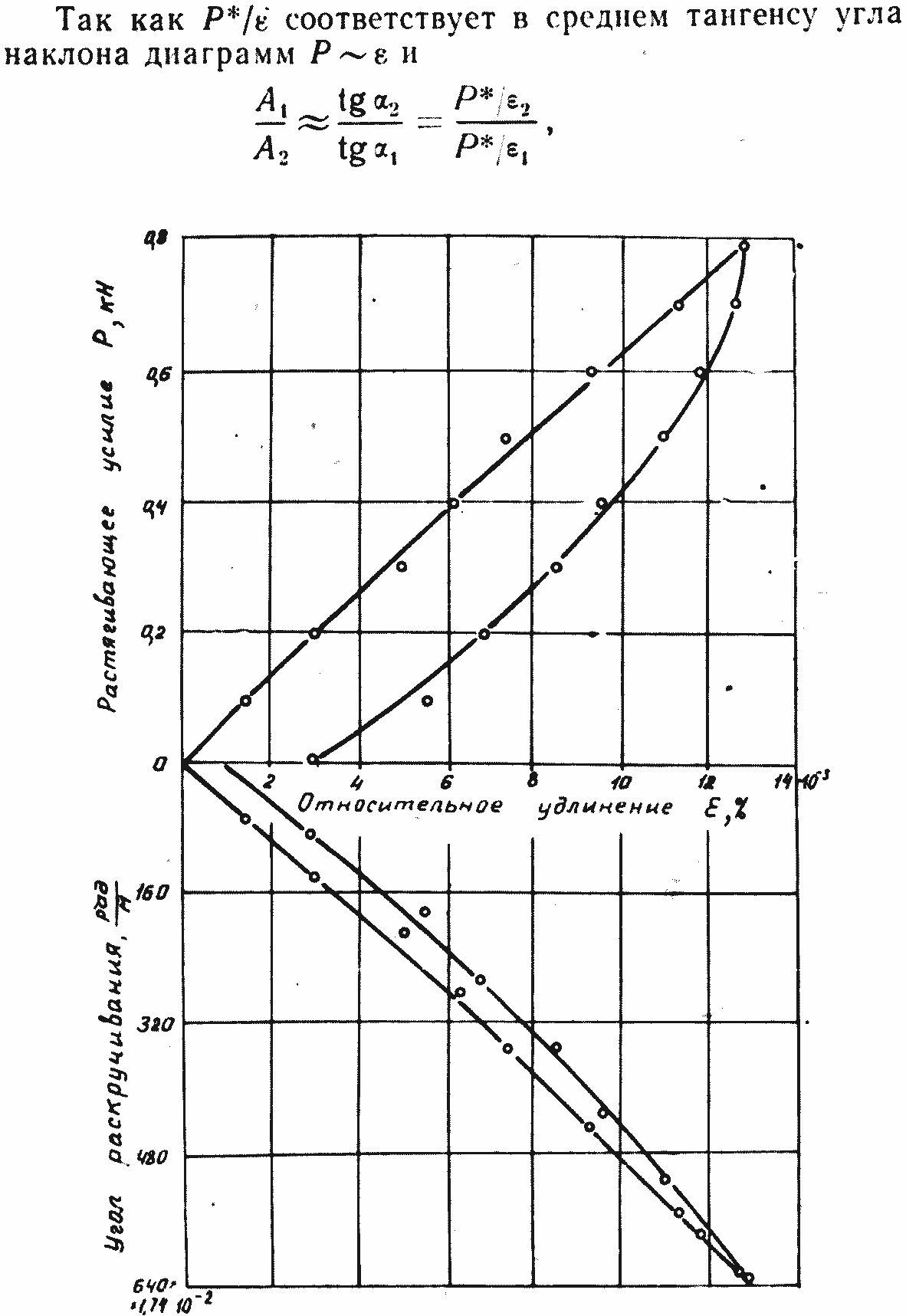
Рис. 1.9. Совмещенные диаграммы Р~ε и γ~ε кабеля КГШ
то, разделив верхнее равенство на нижнее из (1.7), получим (см. рис. 1.4)

Следует отметить, что именно А определено в работе [17]. Значение же А22 определяется при реализации третьего независимого эксперимента при ε=0, γ≠0. Тогда (1.3) дает

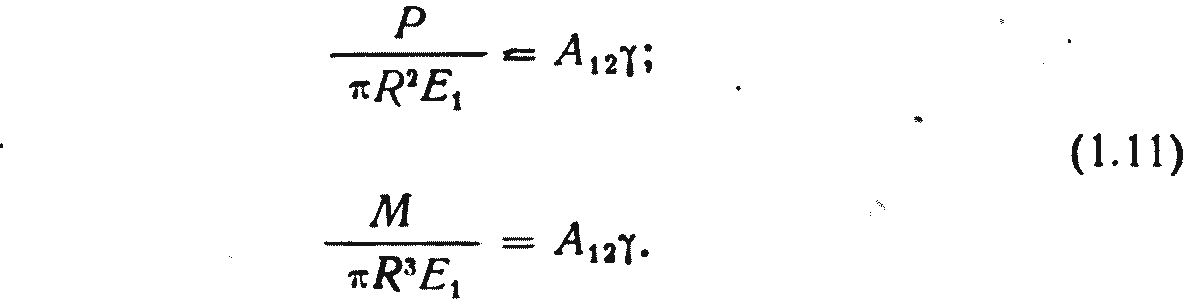
Экспериментальная установка и методика эксперимента по определению жесткости при кручении GI0 описаны в разд. 1.1. Жесткость при кручении GI=B связана с моментом М зависимостью

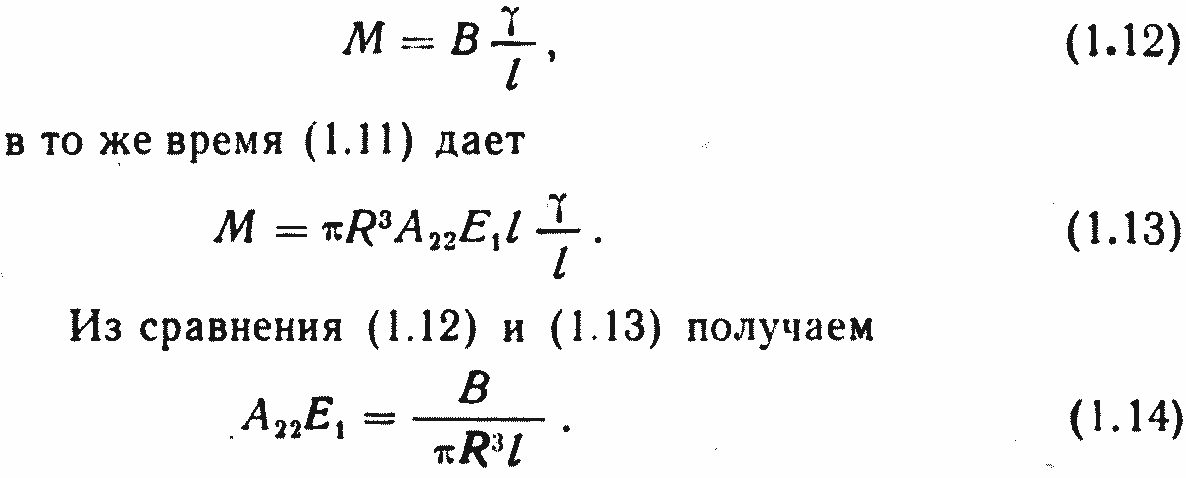
На рис. 1.11 представлены диаграммы М~γ для кабеля КрПТ. Из диаграммы получено значение для В = 200 кг-см². Тогда расчет по формуле (1.14) приводит к результату А22Е1=4,677·105 кг/см².

Таблица 1.2

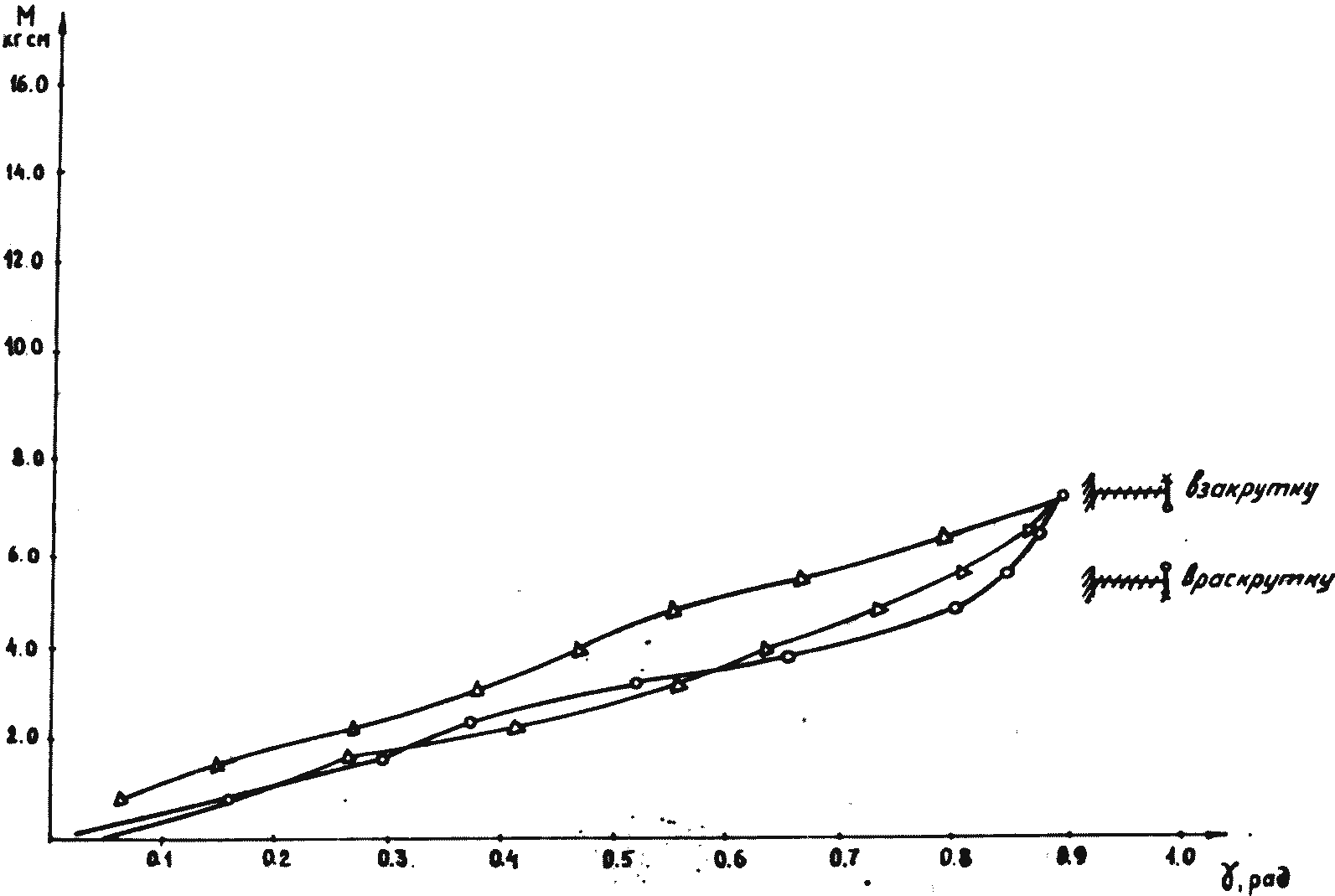
Рис, 1.11. Диаграмма кручения кабеля КРПТ

В табл. 1.2 приведены вычисленные жесткости для каждого из приведенных кабелей. Значение А22 на два порядка выше, чем значение. Зная все модули, находим значения G, E1, v1 при решении алгебраической системы уравнений [15]: