Автоматизированный анализ аварийных ситуаций энергосистем - Принципы построения моделей УРЗА для автоматизированного анализа

ПРИНЦИПЫ ПОСТРОЕНИЯ МОДЕЛЕЙ УРЗА ДЛЯ АВТОМАТИЗИРОВАННОГО АНАЛИЗА ФУНКЦИОНИРОВАНИЯ
Моделирование измерительных органов УРЗА. Любое устройство релейной защиты и автоматики для целей автоматизированного анализа функционирования должно быть представлено соответствующим алгоритмическим (математическим) описанием. Если воспользоваться общепринятой [11] функциональной схемой УРЗА (рис. 5.7), то можно выделить следующие математические методы для ее описания:
измерительные органы (блок 1 на рис. 5.7), которые преобразуют непрерывные входные сигналы (как правило, токи, напряжения и их функции) в дискретные, представляются системами дифференциальных и (или) алгебраических уравнений и неравенств;
остальная часть УРЗА (блок 2), которая преобразует дискретные сигналы и может быть представлена системами логических уравнений.
В рамках данной работы основное внимание будет уделено защитам, реагирующим на вынужденную составляющую токов, напряжений и функций от них при КЗ, на объектах напряжением не более 220 кВ.

Рис. 5.7. Функциональная схема УРЗА:
ИО — измерительные органы; ЛЧ — логическая часть; М — множество выходных сигналов от ИО;К — множество входных логических сигналов ЛЧ
Для таких защит в большинстве случаев измерительные органы могут быть достаточно достоверно представлены системами алгебраических уравнений и неравенств.
В качестве примера можно привести описание измерительного органа сопротивления с характеристикой в форме н-угольника (рис. 5.8).
Если точка Ζ располагается внутри многоугольника или на его границе, то выполняется условие:
(5.8)
в противном случае условие не выполняется
(5.9)
Аналогичные условия существуют и для характеристики в форме окружности (рис. 5.9).
(5.10)
Если выполняется условие (5.10), то точка (Ζ') находится внутри окружности, в противном случае — вне ее. Для объектов без интенсивных переходных процессов времена срабатывания измерительных органов могут быть учтены следующим образом:
вычисляется время выполнения условия срабатывания (например (5.8) или (5.10) для реле сопротивления);
это время сравнивается с заданным и принимается решение о срабатывании реле;
аналогично, после срабатывания, вычисляется условие возврата с учетом коэффициента возврата реле;
вынужденные составляющие электрических величин, на которые реагирует ИО, при моделировании вычисляются поданным ЦО с применением цифровой фильтрации.


Рис. 5.9. Определение условий срабатывания измерительного органа сопротивления (окружность)
Рис. 5.8. Определение условий срабатывания измерительного органа сопротивления (многоугольник)
После определения состояния измерительных органов производится моделирование функционирования логической части защиты. Устройства РЗА относятся к асинхронным конечным автоматам с памятью 112].
Математически такие автоматы представляются следующей системой логических уравнений:
(5.11)
В этом выражении   вектор входных логических переменных в момент времени t + 1. К. понятию времени в этом уравнении обратимся ниже. Вектор выходных логических переменных обозначен Yt+1.  Логические функции обозначены f и φ.
Рассмотрим подробнее понятие времени в смысле системы (5.11). Время в таких системах называют дискретным. Это можно понимать в том смысле, что между моментами времени t+ 1 и t в системе (5.11) не происходит изменений. Изменения происходят только в моменты t е 0, 1,..., п. Это можно проиллюстрировать на примере временной диаграммы (рис. 5.10, 6) для схемы рис. 5.10, а.
Для схемы рис. 5.10 с учетом диаграммы можно составить систему уравнений вида (5.11) по табл. 5.2.
В обозначениях системы (5.11) КА = X, KLt = St, KLt+1 = St+ 1.
В целях упрощения анализа (без потери общности) будем предполагать, что Y= St+ 1. Как правило, это условие выполняется.
Для аналитической записи в дизъюнктивной совершенной нормальной форме (ДСНФ) [12] системы (5.11) можно использовать правило единиц. Для каждой строки, в которой значение функции равно единице, записывается конъюнкция, причем переменная, равная единице,


Рис. 5.10. Схема токовой защиты (а) и временная диаграмма (б)
записывается в конъюнкцию сама, а для переменной, равной нулю, записывается отрицание. Все конъюнкции, полученные для строк, объединяются дизъюнкцией. Так в табл. 5.2 в столбце S две единицы. (5.12)
(5.13)
Таким образом, система (5.11) для схемы рис. 5.10, я имеет вид (5.12). Из алгебры логики известно, что выражения вида (5.13) являются уравнениями триггеров. Таким образом, схема рис. 5.10, я может быть реализована с помощью одного триггера, роль которого в схеме выполняет реле KL. Триггерный эффект определяют задержки на срабатывание и возврат.
Таблица 5.2. Значения логических переменных (состояния контактов реле), соответствующие рис. 5.10

Не вдаваясь в математические подробности, можно отметить, что любое одностабильное реле может быть представлено триггером. Запись в форме табл. 5.2 или в форме системы (5.12) позволяет сделать следующие выводы.
Анализ релейно-контактных схем (РКС), а также временных логических функций вида (5.11), значительно сложнее часто используемого представления таких схем без учета времени. Так в нашем примере (см. рис. 5.13, а) без учета времени система (5.12) вырождается в выражение КА = KL.
Если анализировать все возможные состояния системы (5.12) с учетом любых неисправностей, то придется рассмотреть шестнадцать подобных таблиц (табл. 5.3).
Жирным шрифтом выделена функция, соответствующая схеме рис. 5.10, а.
Часть функций на первый взгляд не имеет смысла. Временная диаграмма для такой таблицы приведена на рис. 5.12.
Такая последовательность событий в схеме рис. 5.10, а может иметь место в случае использования размыкающего контакта при срабатывании его без задержки и возврата с задержкой. Такую последовательность событий в результате неисправностей в схеме рис. 5.10, а можно рассматривать как маловероятную. Следует, однако, заметить, что если уравнение (5.12) реализовано не на электромеханических реле (микропроцессорные защиты), то подобная ситуация может иметь значимую вероятность. Аналогичные рассуждения можно провести для всех S. В качестве примера приведены табл. 5.5 — 5.8 и соответствующие им временною диаграммы (рис. 5.13 — 5.16).
Рассмотренный пример можно несколько усложнить введением в схему еще одного реле (рис. 5.17). Это позволит оценить, как возрастает число возможных последовательностей с ростом числа реле.
Этой схеме и диаграмме соответствует табл. 5.9.
В соответствии с этой таблицей теоретически существует 223 = 256 функций для и столько же для S2. Каждая из функций должна быть проанализирована. В результате часть из них признается возможной и принимается во внимание, а часть отбрасываются, как маловероятная. Число возможных последовательностей для случая срабатывание — возврат каждого реле составит 6! = 720. Выше отмечалось, что для целей анализа функционирования такой отбор может производить модель УРЗА, что значительно ускоряет анализ, так как в качестве эталона выбирается одна последовательность, соответствующая входным переменным состояния измерительных органов и исходному состоянию УРЗА, соответствующему предаварийному режиму.
Таблица 5.12. Наборы значений для области А реле при Кв=/=1

Представление асинхронного автомата синхронным. В приложении 3 показано, что любая схема релейной защиты может быть представлена как асинхронный автомат. Моделирование асинхронных автоматов при большом количестве реле, каждое из которых имеет свою выдержку времени на срабатывание и возврат, весьма затруднительно. Это связано с трудностями разбиения оси времени на большое количество неравномерных отрезков, определяемых этими выдержками времени. Разбиение оси времени целесообразно выполнять с шагом, равным шагу обработки цифровой осциллограммы. Выше отмечалось, что эта обработка осуществляется с шагом < Т. Моделирование должно вестись на каждом шаге, следовательно, синхронное время для моделирования определяется шагом обработки осциллограмм. Гораздо проще представить синхронный автомат, для которого дискретное время равномерно.
Сокращенная таблица

Рис. 5.25. Алгоритм функционирования реле (максимального)
Если разбить ось времени на достаточно малые интервалы времени ΔТ, много меньшие любой выдержки времени, то и получается синхронная ось времени. При этом любая выдержка времени с достаточной степенью точности будет представлена целым числом.
(5.22)
Теперь набор времени срабатывания (возврата) любого реле можно представить счетчиком. Если содержимое счетчика больше соответствующей уставки (Кср, Ки), то реле меняет свое состояние на противоположное. Увеличение содержимого счетчика происходит в том случае, если выполняется условие срабатывания (возврата).
Описание динамического поведения реле статически. Рассмотренным выше принципам представления реле соответствует алгоритм, приведенный на рис. 5.25.
Для функционирования этого алгоритма необходимы следующие данные:
условие срабатывания и возврата реле;
коэффициент возврата;
время срабатывания и возврата реле;
начальное положение реле.
Ниже подробнее рассматриваются эти параметры.
Одностабильные реле (реле тока, напряжения, сопротивления, промежуточные, времени и т.д.), которые рассматривались выше, могут
иметь несколько различные описания. Измерительные органы, для которых существенно значение Кв, целесообразно рассматривать при выполнении условия срабатывания и условия возврата. Сами эти условия определяются системами алгебраических неравенств. Время срабатывания и возврата может задаваться константой (для реле с независимыми
Таблица 5.13. Таблица значений переменных и функций для реле с Кв=1

выдержками времени) или функциями (для реле с зависимыми характеристиками). Уставка реле задается в базе данных, так как она может изменяться в процессе эксплуатации. Собственные параметры реле (К, собственное время срабатывания и возврата для реле без время зависимых характеристик) желательно задавать непосредственно в описании реле.
Таблица 5.14. Сокращенная таблица для реле

Начальное состояние контакта реле должно соответствовать его изображению на схеме в соответствии с ГОСТ (замыкающий — 0, размыкающий — 1). Пример описания реле тока по приведенным правилам: #КА1
Т1 = 0.02 Т2 = 0.035 RELAY ON ABS(la) > ABS(lcp 1) RELAY_OFF ABS(la) < ABS(lcpl * KB) TIMEON T1
TIME_OFF T2
В этом описании знак # определяет начало описания реле с именем (идентификатором) КА1. Константы Т1, Т2 задают время срабатывания и возврата реле соответственно.
АналогичнoTIMEON и TIME OFF определяют время срабатывания и возврата.

Puc. 5.26. Схема токовой отсечки
Действия, производимые после операторов RELAY всегда производятся над комплексными числами.
Допустимы следующие действия: сложение вычитание умножение деление
возведение в степень “Л”
Допускается наличие скобок любой степени вложенности (до 65 000).
Встроенные функции:
“abs” ((аргумент)) — возвращает модуль аргумента;
“ге” «аргумент» — возвращает действительную часть аргумента;
“im” ((аргумент)) — возвращает мнимую часть аргумента;
“ехр «аргумент)) — аналогия
еМ(f— угол в градусах):
“arg” ((комплексное число)) — возвращает угол комплексного числа в градусах (0 — 360).
Для описания логических реле (промежуточных, времени, указательных) может использоваться упрощенная форма. Так как для этих реле Кн значения не имеют, то условие возврата, соответствует условию несрабатывания и наоборот. По этой причине условия возврата (RELAY OFF) может не записываться. Условие срабатывания определяется логическими функциями. Так для схемы рис. 5.26 описания реле KL1 и КН1 имеют вид:
#KLI
Т1 = 0.02 // время срабатывания
Т2 = 0.035
RELAY ON
(КА1 or КА2) and SX9
TIME ON
TI
TIME OFF T2
#KHI
Tl =0. 02 T2 = 0. 035 RELAY ON KLI
TIME ON Tl
TIME OFF T2
Комментарии, следующие та символом “//”, во внимание не принимаются и служат только для персонала.

Рис. 5.27. Пример схемы, число вычислений которой зависит от порядка записи уравнений
Использование операторов RELAY ON, RELAY OFF позволяет вводить описание двухпозиционных реле (триггеров в алгебре логики). К таким элементам относятся выключатели, реле фиксации команды, автоматы и т.д. Ниже будет дан пример такого описания.
Вышеуказанные статические описания порождают с помощью алгоритма приведенные на рис. 5.25 динамические последовательности.
Изложенные принципы описания позволяют “собирать” любую схему защиты. Это может быть релейно-контактная схема, микроэлектронная или микропроцессорная защита. Важно, чтобы были известны условия функционирования измерительных органов и логической части. Для релейно-контактных и микроэлектронных схем УРЗА эти описания могут выполняться по схемам, для микропроцессорных — по функциональным схемам фирм производителей. Такие описания должен уметь анализировать и составлять персонал служб РЗА. Хотя существуют стандартные описания панелей, комплектов и т.д., на каждом конкретном объекте вносятся нестандартные изменения или дополнения. Эти нестандартные решения должны быть внесены в описание.
Учет переходного процесса в логической части защиты при моделировании. Выше уже отмечалось, что в каждом временном сечении моделируется большое количество реле. При этом в схеме могут возникать нежелательные замедления и даже пропуски сигналов, если не учитывать особенностей построения модели. Для примера рассматривается схема, приведенная на рис. 5.27. Для упрощения считаем, что все реле имеют одинаковые выдержки времени на срабатывание и возврат, равные х. В этом случае дискретная ось времени также имеет шаг (рис. 5.28,5.29):

Каждое реле представлено своим счетчиком. Если реле в состоянии “О”, то счетчик набирает выдержку времени на срабатывание. После
срабатывания счетчик сбрасывается и, при выполнении условия возврата, набирает выдержку времени на возврат.
Системы уравнений, описывающие схему на рис. 5.27, записаны в виде:



Рис. 5.29. Временная диаграмма для системы (5.31)
Рис. 5.28. Временная диаграмма для системы (5.24)
(5.25)
(5.26)
(5.27)
(5.28)
(5.29)
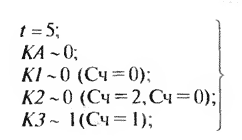(5.30)
Система (5.25) дает состояние схемы при /= 0. В момент t = 1 (5.26) происходит срабатывание КА (от внешних причин, так как это измерительный орган). В счетчик реле А7 записывается “1”, что соответствует началу набора выдержки времени на срабатывание. В момент t = 2 реле К7 срабатывает, так как значение его счетчика 2, т.е. больше уставки. Срабатывание вызывает обнуление счетчика. Счетчик реле К 2 записывает “ 1 ”, так как К 1= 1 Далее все продолжается аналогично для систем (5.28) - (5.30). Временная диаграмма (рис. 5.28) правильно отображает ход событий.
Теперь рассматривается моделирование схемы рис. 5.27, но порядок записи уравнений изменен:
(5.31)
Проведя аналогичные рассуждения для систем уравнений

1. — (5.37) получим временную диаграмму, приведенную на рис. 5.29:

(5.32)
(5.33)
(5.34)
(5.35)

(5.36)
(5.37)
Из диаграммы видно, что реле КЗ вообще не сработало. Из рассмотренного примера можно сделать вывод, что результат моделирования зависит от порядка записи уравнений в системах (5 26), (5.31).
Устранить этот недостаток можно двумя способами. Первый — разбить ось с шагом много меньшим τ, но это в значительной степени увеличит время моделирования (пропорционально уменьшению шага разбиения). Второй — решать каждую из систем (5.32) — (5.37) нс один раз, а до тех пор, пока не перестанут меняться значения счетчиков. Этот способ предпочтительнее, так как увеличение времени моделирования значительно меньше. В этом случае необходимо запоминать значения всех счетчиков на предшествующем шаге. В табл. 5.15 приведено решение системы (5.34) вторым способом.
При заполнении таблицы выполняются следующие правила:
при любом количестве шагов каждый счетчик может измениться только на 1;
Таблица 5.15. Многошаговое решение системы (5.34) для момента времени 1=1

шаги прекращаются, если на предшествующем и текущем шаге все счетчики совпадают.
Сравнение результата, полученного на третьем шаге для (5.34) с (5.27) показывает полное соответствие.
Продолжая аналогичные вычисления для остальных моментов времени (3,4, 5), получим временную диаграмму (см. рис. 5.28).
Зависимость решения от порядка записи уравнений устранена.

Рис. 5.30. Принципиальная схема токовой защиты нулевой последовательности (ТЗНП) и цепи управления выключателем
По рассмотренным правилам можно выполнить в текстовом файле полное описание любой схемы РЗА. Ниже в качестве примера дается описание схемы (см приложение 6, протокол 5.1) четырехступенчатой ненаправленной токовой защиты нулевой последовательности, схемы управления выключателем и АПВ (рис. 5.30).
Приведенный в приложении 5 файл описания содержит все необходимые комментарии, следующие за символом.
Схема взаимодействия программы моделирования с внешними данными приведена на рис. 5.31.
Все необходимые для работы программы моделирования данных формируются логической структурой. База данных (БД) содержит уставки РЗА, положение накладок и перемычек. При любом изменении базы данных запускается программа сканер, которая выбирает данные (только числовые) для программы моделирования. Словарь содержит все необходимые для протоколов имена. Файл осциллограмм и списки идентификаторов входных аналоговых и дискретных сигналов обеспечивают выбор необходимой информации. Необходимо напомнить, что поврежденное присоединение уже определено с использованием дискретной информации (см гл. 4).

Рис. 5.31. Схема взаимодействия timereg с внешними данными

Рис. 5.32. Модельная осциллограмма
Описание алгоритма функционирования — текстовый файл, приведенный выше, соответствует поврежденному присоединению.
Файлы списка защит и присоединений используются для моделирования функционирования всех остальных защит, которые запускались при данной аварии, но нс действовали на отключение выключателей.
Установка модели в предаварийное состояние. Выше отмечалось, что описание модели произведено в предположении отсутствия всех воздействий (токов и напряжений). В предаварийном режиме существуют токи и напряжения.
По этим записям модели РЗА должны установиться в определенное состояние. Эта задача решается путем моделирования функционирования по одному или нескольким начальным сечениям предаварийного режима до тех пор, пока все релейные элементы не будут изменять состояние своих счетчиков в двух соседних шагах, как это было рассмотрено выше. После этого осуществляется движение по всем остальным сечениям.
Программа моделирования может формировать промежуточные результаты (см. приложение 6, протокол 5.2), окончательный протокол (см. приложение 6, протокол 5.3) и соответствующие осциллограммы (рис. 5.32).
Окончательным этапом анализа является сравнение модельной и реальной регистраций событий. При совпадении протоколов (с заданной по времени точностью) выдается комментарий “функционировала правильно”, в противоположном случае кроме комментария “функционировала неправильно” можно просмотреть осциллограммы обеих регистраций.