В современных электрических системах схемы питающих электрических сетей могут быть весьма сложными. Число узлов в них может исчисляться сотнями, а число замкнутых контуров — десятками. В объединенных энергетических системах схемы электрических сетей могут быть еще более громоздкими. Практически расчеты сложных замкнутых сетей могут производиться с помощью автоматических цифровых вычислительных машин (ЦВМ). При весьма сложных схемах в зависимости от назначения расчетов приходится применять специальные методы эквивалентирования схем замещения электрических сетей. Часто в сложных замкнутых сетях имеются линии нескольких различных номинальных напряжений. В этих случаях параметры всех электрических сетей обычно приводят к одному напряжению. При анализе режимов работы сложнозамкнутых электрических сетей и при составлении алгоритмов их расчетов на ЦВМ удобно использовать так называемые матричные методы расчетов. Они основаны на применении алгебры матриц и элементов теории графов. При этом используется аналитическое представление схемы или направленный граф сети. Предварительно фиксируются все характерные элементы сети—ветви, независимые узлы, независимые замкнутые контуры. Они нумеруются; порядок нумерации выбирается произвольно.
При этом для каждой ветви и каждого независимого контура произвольно выбираются и фиксируются определенные положительные направления. Относительно них ориентируются и знаки токов и э. д. с. каждой ветви.
Один из узлов, обычно наиболее мощный источник питания, выбирается в качестве узла баланса. Его мощность заранее неизвестна. Он должен покрыть часть нагрузки потребителей и потерь мощности в сети, не покрытую другими источниками с фиксированным режимом работы. Узел баланса обычно совмещают с базисным узлом, в котором известно напряжение. Параметры одного из узлов зависят от параметров остальных узлов. Поэтому число у независимых узлов на единицу меньше общего числа узлов схемы.
Число независимых замкнутых контуров в замкнутой схеме сети должно соответствовать минимальному числу контурных уравнений, необходимых для определения неизвестных контурных токов. Для остальных замкнутых контуров, называемых зависимыми, соответствующие контурные уравнения могут быть получены путем комбинации контурных уравнений для независимых контуров.
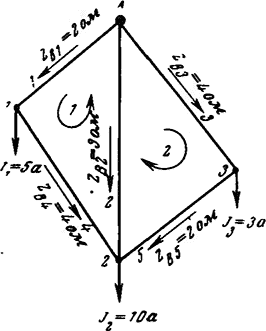
Рис. 2-24. Схема сети с двумя замкнутыми контурами к примерам 2-6 и 2-7.
При аналитическом представлении схемы сети обеспечивается достаточно компактная и наглядная обобщенная запись основных соотношений между параметрами режима, что весьма удобно при выполнении необходимых преобразований и составлении алгоритма решений. Одновременно получается определенная автоматичность в выполнении вычислений. В частности, облегчается программирование расчетов на ЦВМ -вследствие возможности использования стандартных подпрограмм.
Матричные методы расчетов электрических сетей подробно описаны в литературе [Л. 8, 25, 26, 28 и др.]. Ниже дается понятие об основах этих методов. При этом предполагается, что основные сведения из алгебры матриц известны из курса математики. Следует иметь в виду, что применение матричных методов практически целесообразно для достаточно сложных схем замкнутых сетей. Рассмотренные ниже примеры их использования для простейшей замкнутой сети с двумя замкнутыми контурами (рис. 2-24) даны лишь в целях иллюстрации приведенных положений.
Аналитическое представление схем электрической сети производится с помощью так называемых матриц инциденций.
![]()
Первая матрица инциденций М представляет соединение ветвей в независимых узлах схемы. В общем случае матрица М является прямоугольной, число строк ее равно у — числу независимых узлов, а число столбцов — числу ветвей в:
Коэффициент М,j показывает соединение узла i с ветвью / . Он может принимать одно из трех значений: + 1, —1 и 0. Коэффициент Mi, равен положительной единице, если узел i является началом ветви /; отрицательной единице, если узел i является концом ветви, и нулю, если ветвь / не соединена с узлом i.
Таким образом, каждая строка i матрицы М показывает, какие ветви и как по направлению соединены с узлом i схемы. Каждый столбец / показывает, между какими узлами включена ветвь / схемы.
![]()
Вторая матрица инциденций N представляет соединение ветвей в независимые замкнутые контуры схемы. Это прямоугольная матрица. Число ее строк равно числу к независимых контуров схемы, а число столбцов — числу ветвей в схемы:
Коэффициент Ntj показывает соединение ветви / с контуром L Он равен положительной единице, если ветвь / входит в состав контура i и совпадает с ним по направлению; отрицательной — если ветвь / входит в состав контура i с противоположным направлением, и нулю — если не входит.
Каждая строка i матрицы N показывает, какие ветви и как по направлению входят в состав независимого контура схемы. Каждый ее столбец / показывает, в какие контуры и как входит ветвь / схемы.
Очень эффективным при этом оказывается применение итеративных методов расчета. Известно, что итеративные методы расчета основаны на постепенном уточнении результатов приближенного решения. При этом применяется один и тот же алгоритм решения. В связи с этим использование итеративных методов очень удобно при проведении расчетов на ЦВМ.
Для нелинейных схем в случае нагрузок, заданных мощностями, решение резко усложняется. Для получения решения приходится применять соответствующие итеративные методы или производить линеаризацию схем замещения.
В настоящее время существует значительное количество методов определения параметров режима сложнозамкнутых сетей, а также специальных приемов, уменьшающих вычислительную работу и ускоряющих процесс решения. Применение тех или иных методов и приемов расчета может быть более или менее эффективным в зависимости от сложности сети и характера решаемой задачи.
Ниже в целях иллюстрации показано применение контурного уравнения. При этом приведено решение в общем виде, а также дано решение, удобное для приближенных расчетов (первого этапа) вручную. Оно может быть использовано для расчетов сравнительно несложных нелинейных схем напряжением 110—220 кВ.
При определении параметров режима часто бывает целесообразно использовать разделение замкнутой схемы сети на дерево и хорды. Деревом схемы называют ее разомкнутую часть, соединяющую узел баланса со всеми независимыми узлами. Число возможных деревьев для каждой схемы может быть достаточно большим. Хордами называют остальные ветви замкнутой схемы.
Добавление каждой из хорд к дереву схемы приводит к созданию одного независимого замкнутого контура.

