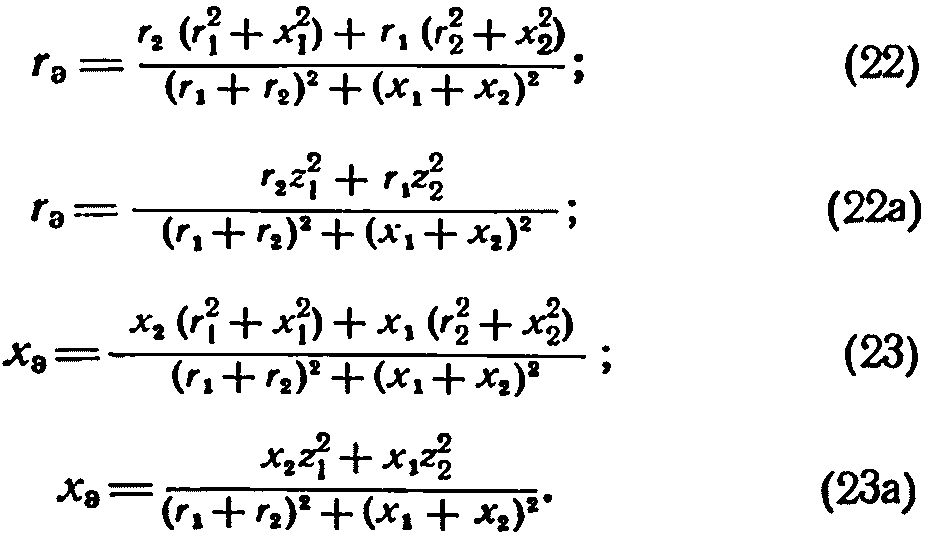Полное сопротивление z какого-либо участка сети является геометрической суммой активного r и индуктивного х сопротивлений и определяется как
Поэтому при определении полного сопротивления цепи до места к. з. необходимо отдельно определить суммарное активное сопротивление r ς , отдельно суммарное индуктивное сопротивление z ς , затем найти их геометрическую сумму как
. Если же определить r=
для каждого элемента сети и затем найти их арифметическую сумму, то величина полного сопротивления будет преувеличенной, а значение тока короткого замыкания—преуменьшенным.
Численно одинаковые результаты могут быть получены только в одном частном случае, когда отношение r/x для всех участков сети одинаково. В действительных же сетях это отношение всегда различно для разных участков. Так, полное сопротивление системы и сопротивление крупных трансформаторов практически равны их индуктивному сопротивлению.
Отношение активных и индуктивных сопротивлений линий 6—35 кВ с проводами А-70, А-95, AС-70, AС-95 и медными М-50, М-70 близко к единице.
Отношение r/x для линий с проводами, имеющими небольшое сечение (А-25, А-16), равно примерно 2—3, а для стальных проводов r/х во много раз больше.
Рис. 5. Графическое определение сопротивлений к примеру 6. а — правильно; б — неправильно.
До сих пор речь шла об определении суммарного полного сопротивления для цепи, состоящей из нескольких сопротивлений, включенных последовательно. В сетях часто встречается параллельное включение двух или нескольких сопротивлений. Эквивалентное сопротивление такой схемы определяется по следующему выражению:
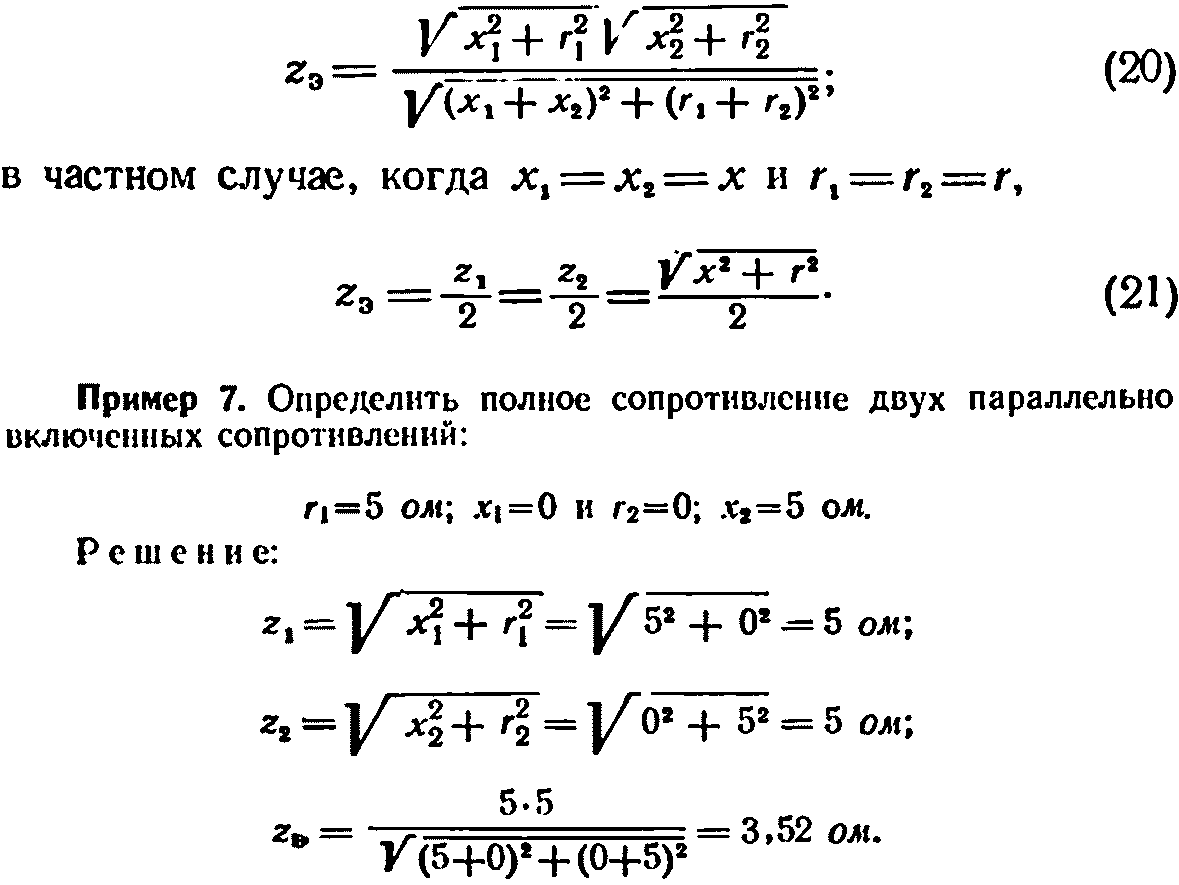
Эквивалентные активные и реактивные сопротивления цепи, состоящей из двух параллельно включенных сопротивлений, определяются согласно следующим выражениям:
