Векторные диаграммы трансформатора

Уравнения трансформатора (16) могут быть решены аналитическим или графическим методом. Графический метод решения основан на построении векторных диаграмм. Он является более наглядным и часто используется для качественного анализа различных режимов работы трансформатора.

Режим холостого хода

В режиме холостого хода первичная обмотка трансформатора включена в сеть на напряжение , а вторичная разомкнута . Для этого режима справедливы уравнения

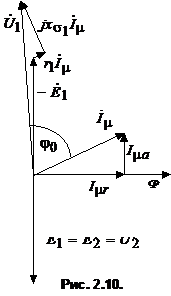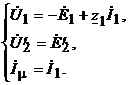                            (17)
Ток первичной обмотки представляет собой намагничивающий ток трансформатора. Построение векторной диаграммы (рис.10) начинают с вектора потока . ЭДС  и  отстают от потока на угол 90°. Реактивная составляющая тока намагничивания  совпадает по фазе с потоком, а его активная составляющая опережает поток на 90°. Намагничивающий ток  несколько опережает поток . Для получения вектора первичного напряжения необходимо построить вектор  и прибавить к нему падения напряжений на активном  и индуктивном  сопротивлениях. Из векторной диаграммы видно, что  очень мал. Обычно . Трансформатор потребляет из сети реактивную мощность на создание магнитного поля в трансформаторе.

Режим короткого замыкания

Режимом короткого замыкания называют режим при замкнутой накоротко вторичной обмотке . Схема замещения трансформатора в этом режиме имеет вид, представленный на рис. 11. Для режима короткого замыкания справедливы следующие уравнения:

Векторная диаграмма (рис. 12) в этом режиме строится аналогично векторной диаграмме для режима холостого хода. Угол  определяется параметрами вторичной обмотки:
.
Особенность этого режима состоит в том, что ЭДС  значительно отличается от напряжения  из-за больших токов короткого замыкания. Учитывая, что , током  можно пренебречь. Тогда схема замещения может быть упрощена (рис. 13).
Из схемы замещения получаем
.
Если принять, что , то действующее значение ЭДС  будет равно половине действующего значения напряжения :

.
Поэтому в режиме короткого замыкания магнитопровод трансформатора оказывается ненасыщенным.
Действующее значение тока короткого замыкания в соответствии с рис. 13
,
где  - модуль комплексного сопротивления короткого замыкания трансформатора.
При  ток короткого замыкания может превосходить номинальное значение в 10-50 раз. Поэтому в условиях эксплуатации режим короткого замыкания является аварийным. Однако этот режим часто проводится при пониженном напряжении для определения параметров трансформатора.
Напряжение , при котором ток короткого замыкания равен номинальному, называется напряжением короткого замыкания и обозначается
.
Отсюда следует, что напряжение короткого замыкания  представляет собой падение напряжения на внутреннем сопротивлении трансформатора при номинальном токе и поэтому является важной характеристикой трансформатора.
Если совместить вещественную ось с вектором тока , то комплексное значение  можно представить как , где ,  - активная и реактивная составляющие напряжения короткого замыкания. Обычно модуль  выражают в относительных единицах,
,
либо в процентах,
.
Величина  оказывает существенное влияние на свойства трансформатора в рабочих и аварийных режимах. Поэтому  является паспортной величиной наряду с номинальными данными.

Режим нагрузки трансформатора

Векторные диаграммы при нагрузке строят по уравнениям (16). Вид векторной диаграммы зависит от характера нагрузки (рис. 14).

Векторная диаграмма а рис. 14 соответствует активно-индуктивной нагрузке, а векторная диаграмма  б - активно-емкостной нагрузке.
Сопоставляя обе диаграммы, можно заключить, что при  и  увеличение активно-индуктивной нагрузки вызывает снижение напряжения , а при увеличении активно-емкостной нагрузки напряжение  возрастает. Это объясняется тем, что при активно-индуктивной нагрузке происходит некоторое размагничивание трансформатора (поток Ф уменьшается, так как ток  имеет составляющую, направленную навстречу току ), а при активно-емкостной нагрузке трансформатор дополнительно намагничивается (поток Ф возрастает, так как ток  имеет составляющую, совпадающую с ).

Для оценки диапазона изменения напряжения  вводится величина , представляющая собой арифметическую разность между вторичным напряжением трансформатора при холостом ходе () и при номинальной нагрузке (). Напряжение первичной обмотки принимается постоянным и равным номинальному .
.                       (18)
Для расчета  примем допущение , тогда, используя
упрощенную схему замещения (рис.15), получим
.                              (19)
Уравнению (19) соответствует векторная диаграмма, представленная на рис. 16. Из векторной диаграммы следует, что

.

Подставляя приближенное выражение для  в уравнение (18), получим
.
Отрезок  можно выразить через составляющие напряжения короткого замыкания:

,

где . Учитывая, что , , получим для  простое выражение
.
На рис. 17 представлена зависимость  при .
Максимальное снижение напряжения имеет место при , а при  напряжение  не зависит от нагрузки.