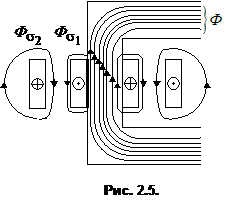|
Реальное магнитное поле трансформатора имеет довольно сложный характер. С целью упрощения анализа магнитное поле разделяют на поле взаимной индукции, трубки которого замыкаются по стальному сердечнику и образуют поток Ф, и поле рассеяния, которое обусловливает потоки ![]() и
и ![]() , каждый из которых сцеплен только со своей обмоткой (рис.2.5). Магнитное поле взаимной индукции можно рассчитать с помощью закона полного тока. Для любого контура, полностью замыкающегося по стальному сердечнику, имеем
, каждый из которых сцеплен только со своей обмоткой (рис.2.5). Магнитное поле взаимной индукции можно рассчитать с помощью закона полного тока. Для любого контура, полностью замыкающегося по стальному сердечнику, имеем
![]() .
.
Уравнение упрощается, если принять допущение о равномерности магнитного поля по сечению магнитопровода ![]() :
:
![]() .
.
Введем обозначения: ![]() - МДС первичной обмотки;
- МДС первичной обмотки; ![]() - МДС вторичной обмотки;
- МДС вторичной обмотки; ![]() - результирующая МДС. И учитывая, что
- результирующая МДС. И учитывая, что ![]() , получим
, получим
 , (2.4)
, (2.4)
где ![]() - магнитное сопротивление;
- магнитное сопротивление; ![]() и
и ![]() - длина и площадь поперечного сечения магнитопровода
- длина и площадь поперечного сечения магнитопровода
Выражение (2.4) можно трактовать как закон Ома для магнитной цепи: МДС аналогична ЭДС, поток - току, магнитное сопротивление - электрическому сопротивлению.
Если выразить результирующую МДС ![]() через ток намагничивания
через ток намагничивания ![]() ,
,
![]() ,
,
то получим уравнение магнитной характеристики трансформатора без учета потерь
![]() . (2.5)
. (2.5)
Поток Ф образует с первичной обмоткой потокосцепление ![]() , а со вторичной -
, а со вторичной - ![]() ;
;
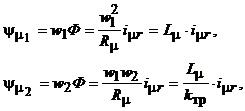
где ![]() - взаимная индуктивность первичной обмотки;
- взаимная индуктивность первичной обмотки; ![]() - коэффициент трансформации.
- коэффициент трансформации.
Магнитные поля рассеяния образуют потокосцепления рассеяния соответствующих обмоток:
![]() ;
;
![]() ,
,
где ![]() и
и ![]() - индуктивности рассеяния первичной и вторичной обмоток соответственно.
- индуктивности рассеяния первичной и вторичной обмоток соответственно.
Индуктивности рассеяния обмоток трансформатора значительно меньше взаимной индуктивности ![]() , так как определяются потоками рассеяния, замыкающимися, главным образом, по немагнитным участкам (рис. 2.5). По этой же причине индуктивности
, так как определяются потоками рассеяния, замыкающимися, главным образом, по немагнитным участкам (рис. 2.5). По этой же причине индуктивности ![]() и
и ![]() можно принять постоянными, в то время как взаимная индуктивность
можно принять постоянными, в то время как взаимная индуктивность ![]() зависит от степени насыщения стали
зависит от степени насыщения стали ![]() .
.