Расчет электростатических полей высокого напряжения методом эквивалентных зарядов

УДК 621.319.7.027.3     ·

 Изоляция электрооборудования высокого напряжения и вентильные разрядники. Труды ВЭИ, 1982, вып. 91, с. 59—68.
Представлены результаты расчета электростатических полей промежутка стержень — плоскость и генератора импульсных напряжений. Показана эффективность модифицированного метода для многоэлектродных систем.
Библиогр.: 5.

В. E. Бобиков, А. А. Гycapoe
РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ КОНСТРУКЦИЙ ВЫСОКОГО НАПРЯЖЕНИЯ МОДИФИЦИРОВАННЫМ МЕТОДОМ ЭКВИВАЛЕНТНЫХ ЗАРЯДОВ
Интенсивное развитие электротехники требует от исследователей все более полного анализа разрабатываемого оборудования. Проведение такого анализа только экспериментальным путем требует больших материальных затрат и увеличивает время на разработку. Использование численного эксперимента позволяет провести значительную часть исследования на ЭВМ и повышает эффективность и качество разработок. При разработке математической модели для предполагаемого исследования необходимо стремиться к наиболее полному математическому описанию объекта исследования, а это в свою очередь требует привлечения эффективных численных методов.
При расчете электростатических полей такими методами являются методы конечных разностей (МКР), конечных элементов (МКЭ) и эквивалентных зарядов. Каждый из них имеет как преимущества, так и недостатки. Так, при расчете в областях со сложной границей методом конечных разностей в расчетной сетке появляются иррегулярные узлы, которые часто приводят к потере точности расчета. Введение неравномерного разбиения области в целях учета физических особенностей конкретной задачи приводит к усложнению разрешающего алгоритма задачи. При расчете внешних задач приходится вводить искусственные границы на расстоянии, равном пяти размерам интересующей нас области, что сильно завышает время расчета и загружает оперативную память ЭВМ.
Метод конечных элементов позволяет точнее, чем МКР, учитывать конфигурацию рассматриваемого пространства, однако при расчете внешних задач имеет также недостатки.

Рис. 1. Система электродов стержень — плоскость
В последнее время при расчетах электростатических полей конструкций высокого напряжения популярность приобрел метод эквивалентных зарядов, который лишен указанных недостатков. Этот метод предполагает решение системы алгебраических уравнений вида:
0
где- матрица потенциальных коэффициентов;— вектор
неизвестных зарядов;    — вектор потенциалов.

Введение в метод целевой функции от зарядов и их координат [1 ] повышает его эффективность.
Целевая функция для системы эквивалентных зарядов имеет следующий вид:


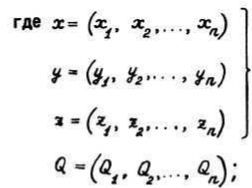
координаты эквивалентных зарядов;
n— количество эквивалентных зарядов; m — количество контурных точек на поверхности проводника.
Если рассматривать задачу минимизации функции (2) только по зарядам, то, продифференцировав целевую функцию, получим систему уравнений (1), т. е. задачи (1) и (2) в этом случае эквивалентны. При рассмотрении резконеоднородных полей достаточно трудно определить подходящее расположение и количество эквивалентных зарядов. Поэтому целесообразно проводить минимизацию не только по зарядам, но и по координатам их местоположения. Такой подход позволяет с любой заданной точностью рассчитывать электростатическое поле для многих практических задач электротехники. Ниже приводятся расчеты электрических полей двух характерных для техники высоких напряжений систем электродов.
Расчет электростатического поля электродов стержень — плоскость. Во многих электрофизических исследованиях коронных разрядов, механизма пробоя различных диэлектриков и т. д. возникает необходимость в расчете полей электродов в виде стержень — плоскость (рис. 1).
Данная задача рассматривалась различными авторами, она стала как бы тестовой задачей для каждого метода. Методом эквивалентных зарядов эта задача впервые была решена в [2]. Однако трудность выбора удачного расположения зарядов, очевидно, объясняется ограничением размера промежутка G/R = 200+50. Поэтому в [3] для промежутков 10—1 был применен метод конечных разностей. В работе [4] методом эквивалентных зарядов эта задача была решена для всего диапазона изменений расстояния стержня до плоскости, но, к сожалению, нет данных о расположении эквивалентных зарядов, приведена только зависимость коэффициента использования от межэлектродного расстояния. Поэтому, не останавливаясь подробно на этой задаче, здесь приводятся только данные о расположении зарядов и зависимости напряженности на всем промежутке, полученные методом эквивалентных зарядов с использованием целевой функции. Система эквивалентных зарядов представлена точечным зарядом вблизи центра полусферы и полубесконечными линейными зарядами, лежащими вдоль осевой линии стержня. На поверхности стержневого электрода выбиралось произвольно т. контрольных точек, в месте закругления стержня их частота была увеличена.
В цилиндрической системе координат целевая функция

где Uo — потенциал проводника; Ui— потенциал, вычисленный в ι-й контрольной точке; Q — элементарный заряд.
Начальный вектор переменных [r, ,z Q находился из (1) методом наименьших квадратов, где за неизвестные принимались только заряды.

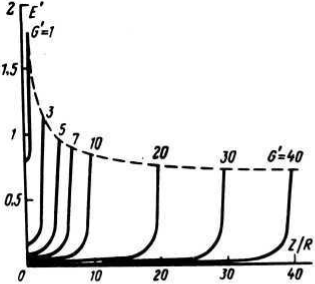
Рис. 2. Относительные значения напряженности поля Е'на оси при различной длине промежутка G=G/R

Определение точки минимума данной функции дает значения зарядов и их координат.
При расчете G/R= 200 оказалось возможным сократить количество линейных зарядов с 9 до 7. При этом точность выполнения граничных условий составила меньше 1%. Это говорит о том, что в работе [1] использовалась не оптимальная система эквивалентных зарядов. Для расчета промежутков с различными значениями G/R число полубесконечных нитей изменялось от 7 до 9, число контурных точек бралось равным 17. Расчеты проводились на ЭВМ ЕС-1020.
Полученные в результате расчетов кривые распределения относительной напряженности поля E=ER/U воздушных промежутков по осевой линии приведены на рис. 2. Пунктиром отмечена линия максимальной напряженности поля. Координаты элементарных зарядов и их значения для малых межэлектродных промежутков приведены в табл. 1. Используя данные этой таблицы, можно достаточно быстро рассчитать значение напряженностей и потенциала для любых соотношений G/R в этом диапазоне.
Из приведенного примера видно, что введение целевой функции в метод эквивалентных зарядов позволяет рассчитывать электрические поля простых электродных систем (стержень — плоскость , шар — стержень и т. д. ) для всего диапазона изменений межэлектродного промежутка.
Расчет напряженностей на экранах оборудования высокого напряжения. Повышение уровня напряженности линий электропередачи привело к необходимости создания и строительства испытательного оборудования на сверхвысокие напряжения. В связи с этим большое значение уделяется расчету электростатических полей различных вариантов исполнения такого оборудования высокого напряжения.
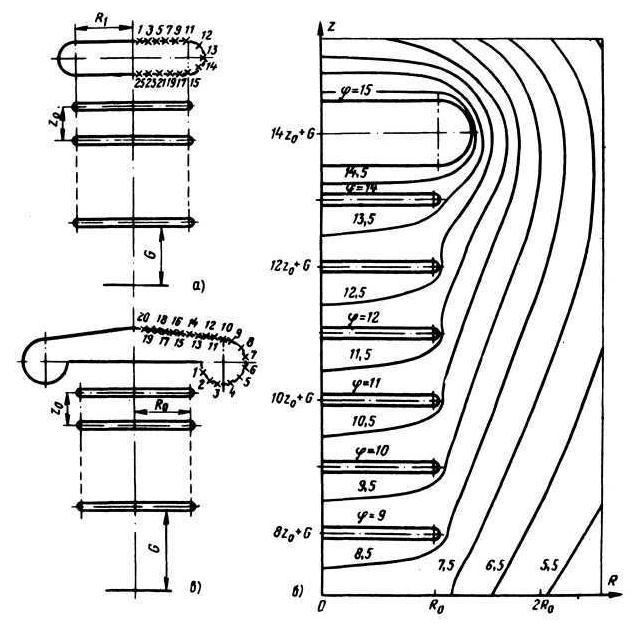
Знание напряженностей на поверхности экранов позволяет сравнивать их различные варианты и выбирать наиболее целесообразные в отношении электрических, экономических и прочих показателей. Ниже на основе электростатических полей сравниваются два варианта исполнения верхнего экрана генератора импульсных напряжений (ГИН) (рис. 3,а,в).
При многоэлектродных системах с различными условиями в целевую функцию (3) вводится весовой коэффициент β=1/U. Это позволяет сократить время на минимизацию функции и точнее выполнить граничные условия на каждом из экранов.

Таблица 1

В качестве элементарных зарядов использовались тороидальные нити [5] и плоские заряженные диски [1] с распределением заряда согласно

где б — поверхностная плотность заряда; Q — полный заряд диска; r — радиус диска.

Потенциал, создаваемый в любой точке пространства заряженным диском, определяется по выражению

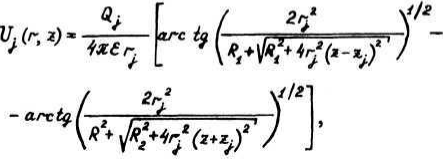
Рис. 3. Экраны высокого напряжения и картина электростатического поля ГИН

Поверхностный заряд каждого межэтажного перекрытия заменялся двумя плоскими заряженными дисками и одной тороидальной нитью. На каждом из объемных дисков бралось 25 контурных точек, из них 5 на закруглении. Минимизирующая функция имела вид:
(У
где U0k— потенциал каждого этажа; т — количество этажей; n — количество контрольных точек на этаже.
Проверка точности решения проводилась в 50 контурных точках на каждом межэтажном перекрытии и экранах высокого напряжения. Погрешность выполнения граничных условий по потенциалу составила менее 1 и 2% соответственно. Полученная картина электростатического поля ГИН (вариант 1) приведена на рис. 3,б. Расчет напряженностей для заряженных дисков проводился по формулам:

Относительные напряженности (, где R — радиус закругления этажа; U - разность потенциалов между этажами) для двух вариантов исполнения ГИН высокого напряжения сопоставляются в табл. 2. Второй вариант экрана высокого напряжения гораздо предпочтительнее в электрическом отношении, чем первый.

Таблица 2

Кроме того, в этом случае возможно применение и полиэлектродного экрана, т. е. экрана, состоящего из многих одиночных дисков. Такой экран обладает рядом преимуществ: он легок, экономичен и прост в изготовлении. Хотя максимальная напряженность поля такого экрана и выше на 20-60% [5] , для второго варианта это вполне допустимо.
В процессе исследования оказалось возможным выявить закономерность в расположении эквивалентных зарядов при расчете подобных устройств высокого напряжения с любым количеством этажей (при исполнении верхнего электрода по первому варианту). Использование данных табл. 3 при решении уравнения (1) методом наименьших квадратов позволяет получить погрешность расчета, не превышающую 3%.

Таблица 3

Расчеты проводились на ЭВМ ЕС-1020, время счета каждого из вариантов при использовании целевой функции (4) составило 46 мин, при использовании данных табл. 2—12 мин. Во всех примерах для минимизации целевой функции использовались подпрограммы математического обеспечения FMFP и FMCG, основанные на методах Давидона и сопряженных градиентов соответственно.
Список литературы

1. Гусаров А. А., Бобиков В. Е. Расчет электростатических полей методом эквивалентных зарядов. — Электричество, 1979, № 2, с. 65—66.
2. Abou-Seada M.S., Nasser Е. Digital Computer Calculation of the Potential and Field of Rod Gap. — Proc. IEEE, 1968, vol. 56, №5, p. 813-820.
3. I s a X. Field Analysis of Sphere—Sphere and Rod—Plane Gaps and Its Application to Calculation of'Breakdow Voltage. - Electr. Engng in Japan, 1971, Bd 91, № 5, p. 89-100.
4. SteinbigIer H. Digitale Berechung etektrisher Felder. — Electrotechn. Z„ 1969, Bd 90, № 25, p. 663-666.
5. Singer H., Steinbigler H., Weiss P. The simulet ion method for the calculation of high voltage fields. — IEEE Trans. Power Appar. and Syst., 1974, Bd 3, p. 1660-1668.