Гидравлика зданий ГЭС - Расчет эжекции в нижний бьеф

8-3. РАСЧЕТ ЭЖЕКЦИИ В НИЖНИЙ БЬЕФ
Эжекция в нижний бьеф осуществляется сбросом рабочего (эжектирующего) потока в нижний бьеф через водосбросы различного типа. При этом турбинный (эжектируемый) поток выходит из отсасывающей трубы либо под водосбросную струю, либо сбоку от нее. Расчетные формулы в этих случаях несколько различаются.
Различаются расчетные формулы и в зависимости от режима сопряжения бьефов. Поэтому расчетам эжекции должны предшествовать расчеты критических режимов.
388

При известных пьезометрических напорах в выходном сечении отсасывающей трубы (отсчитываемых от сливной кромки уступа) при эжекции и без таковой эффект эжекции по напору может быть вычислен как разность: 1) пьезометрических напоров; 2) пьезометрических уровней, отвечающих этим напорам; 3) пьезометрического эффекта эжекции и перепада восстановления:
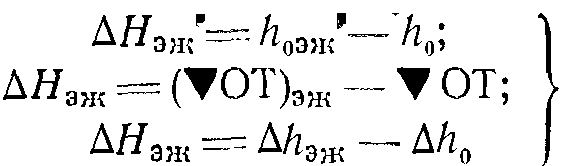(8-4)
или как разность напоров по формуле (8-1), причем Нт.эж может быть вычислен по формуле (2-7), а Нт—по формулам (2-6) — (2-6").
Нахождение пьезометрического напора в выходном сечении отсасывающей трубы при отсутствии эжектирующего потока рассматривается в гл. 2. В настоящей главе рассмотрим способы определения пьезометрического напорав выходном сечении отсасывающей трубы при эжекторовании.
Основными уравнениями для отыскания пьезометрического напора являются уравнения Бернулли и уравнение количества движения (6-39), составленные для некоторых сечений и отсеков потока, прошедшего через здание ГЭС.

а) Эжекция при сбросе воды через водослив

Исходным для получения формул, связывающих пьезометрический напор h0 и глубину нижнего бьефа t, остается уравнение (6-39). . Для упрощения несколько изменяем выражения некоторых сил в сечении 1—1 на рис. 6-27. Так, при донном режиме силу давления в струе в створе уступа принимаем равной, что отвечает эпюре давления в виде не зависящего от h0 треугольника (рис. 6-24), а силу давления на торцы быков

Для донного режима получаем следующие формулы.

При падении струи на наклонный участок водобоя

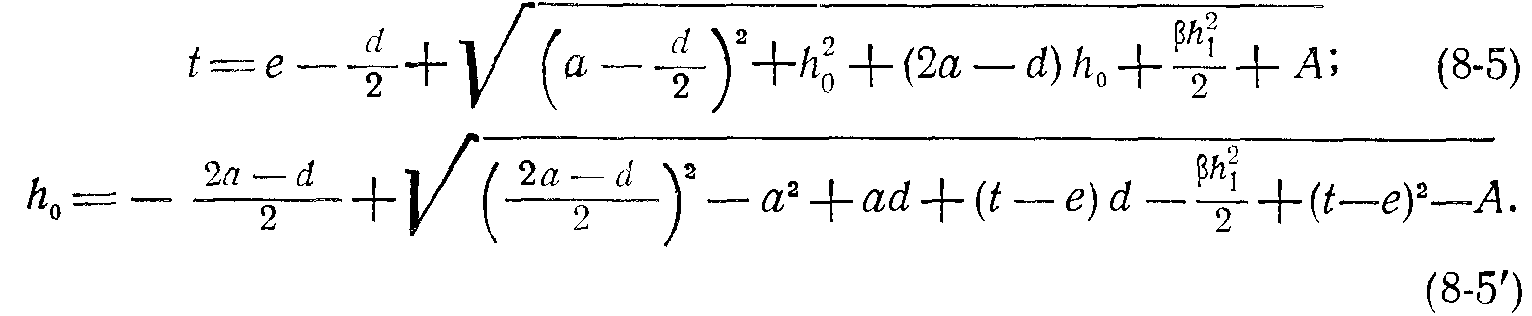
При падении струи за наклонный участок водобоя, т. е. при наклонном участке в пределах донного вальца:

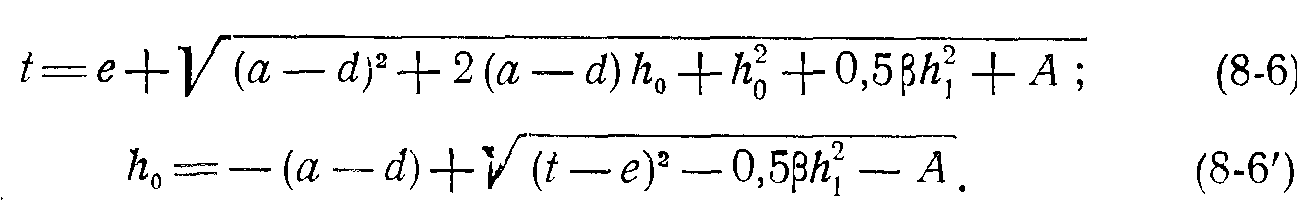
Эти формулы не изменяются при наличии на водосливе дополнительного быка, в котором размещена турбинная шахта, поскольку за ширину b принимается ширина водослива на сливной кромке носка.
Приформулы действительны при условии обеспечения свободного доступа воздуха под струю в створе уступа.
Обозначения в формулах остались прежними (рис. 6-27), член А вычисляется по формуле (6-52).

ГДе ∆t — превышение свободной поверхности нижнего бьефа на рисберме над сливной кромкой носка; qB — удельный расход на сливной кромке водослива в кубических метрах в секунду.
В настоящее время не разработан способ расчета эжекции при донном восстановленном, а также при поверхностном восстановленном режимах. При этих режимах для расчета h0, так же как и при затопленном поверхностном прыжке, не хватает данных для определения глубины на уступе и скорости в сечении сливной кромки уступа.
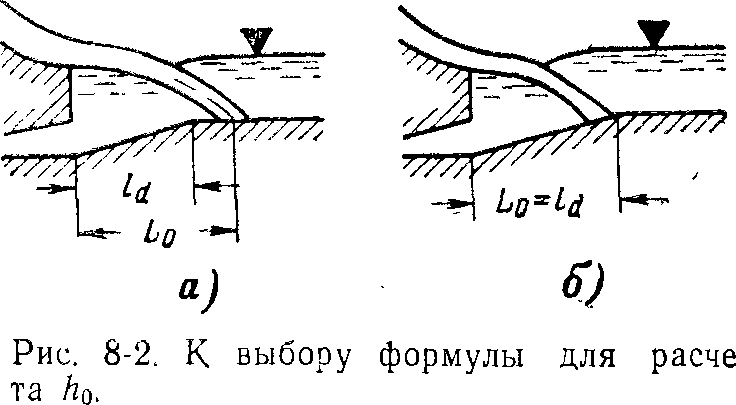
При выборе расчетной формулы требуется знать, находится ли наклонный участок в пределах донного вальца или частично вне донного вальца, т. е. оказывает ли сбросная струя непосредственное динамическое воздействие на наклонный участок. Ответ на этот вопрос в первом
приближении можно найти, используя формулы Μ. Ф. Складнева (табл. 6-8) или формулы § 6-9.
Ответить на вопрос, будет ли падать струя за наклонный участок или на наклонный участок, можно, используя формулы дальности отлета свободной струи (6-98), (6-103), (6-104). Если из этой формулы следует, что свободная струя отлетает за наклонный участок (рис.8-2,а), то, так как при h0>hi дальность отлета струи увеличивается, наклонный участок водобоя будет определенно в области донного вальца. Если же в соответствии с расчетом свободная струя падает в конце наклонного участка (рис. 8-2,б) или в начале горизонтального участка, то подтопленная струя при h0<h1 будет падать на наклонный участок водобоя.

б) Эжекция при сбросе воды через напорные водосбросы

Здесь А определяется, как и ранее, по формуле (6-52).

При донном режиме расчет эжекции при сбросе воды через напорные водосбросы можно вести по тем же формулам, что и при сбросе
через водосливы. Во всех случаях h1 есть высота водосбросных отверстий в свету. Формулы остаются в силе при отсутствии промежуточных быков в конце водосбросов. Если промежуточные быки имеют длину, одинаковую с основными быками, то В0 следует принимать равной суммарному расстоянию между быками в свету.

в) Эжекция при сбросе воды по бокам отсасывающей трубы

Эжекция при сбросе воды по бокам отсасывающей трубы может осуществляться при отсутствии уступа у водосливов или напорных водосбросов, между которыми расположен агрегат, и при наличии уступа.
Расчетная формула для случая отсутствия уступа по бокам отсасывающей трубы дана Креем [96].
Водосбросы но бокам отсасывающей трубы могут представлять собой подтопленные водосливы с широким порогом или напорные водосбросы с отверстиями, имеющими пороги на уровне дна отводящего русла. Во втором случае, а также при истечении из-под затвора в конце водослива с широким порогом в нижнем бьефе будет иметь место донный затопленный прыжок. Это обстоятельство, а также неравномерность распределения скоростей в сечениях, выделяющих при составлении уравнения количества движения отсек нижнего бьефа, формулой Крея не учитывается.

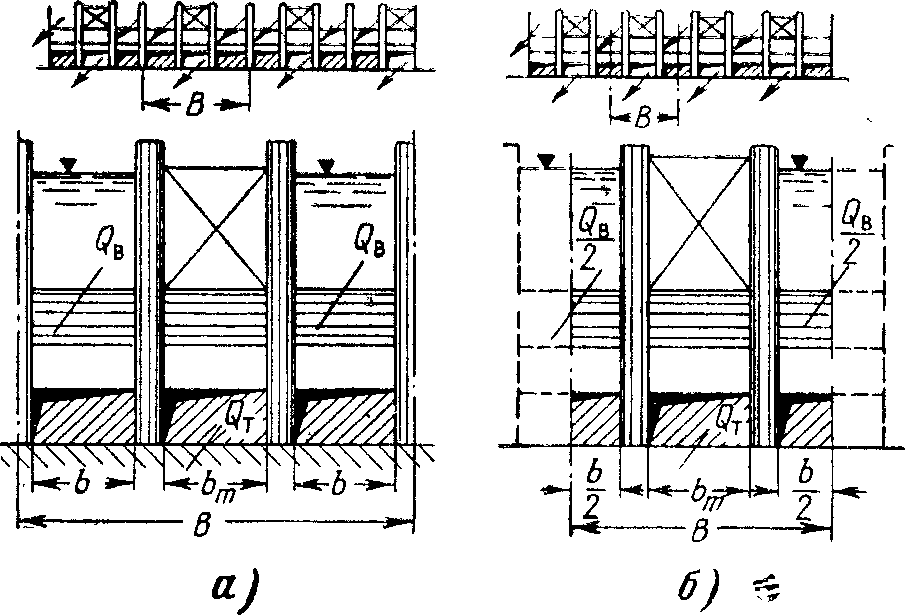
Рис. 8-3. К расчету эжекции при сбросе воды по бокам отсасывающей трубы.
а — сброс при открытии пролетов по два через один; б — при открытии пролетов через один.
Ранее нами была рассмотрена эжекция при сбросе воды через водосливы по бокам отсасывающей трубы [239] на примере водосливной ГЭС при открытии по два водосливных отверстия через одно или чередовании открытых и закрытых отверстий (рис. 8-3). Опытами на модели трех блоков было установлено, что если быки, разделяющие турбинные блоки, значительно короче водоворотных областей под водосбросными струями, то давление в отверстии отсасывающей трубы и в створе уступов выравнивается, т. е. vOT = y/z0. Поэтому для случаев, соответствующих схемам, изображенным на рис. 8-3, при донном режиме могут быть использованы формулы (8-5), (8-6), а при поверхностном режиме — формулы (8-7) — (8-9). Формулы также применимы при работе всех турбин и чередовании открытых и закрытых отверстий.

г) Влияние на эффект эжекции диффузорной камеры и эжекторной балки

При использовании диффузорной камеры расход, проходящий через водосбросы, увеличивается (§ 7-8). Но одновременно вследствие увеличения размеров отверстия, из которого поступает в нижний бьеф сбросной расход, снижается скорость потока и несколько возрастает коэффициент количества движения в этом сечении. Отношение приращений количества движения для отсека отводящего русла при наличии и отсутствии камеры близко к единице, что говорит о малом влиянии камеры на эффект эжекции в нижнем бьефе.
Эжекторная балка конструктивно схожа с диффузорной камерой без козырька (рис. 7-28,а, е, ж и др.), у которой отсутствует дно, разделяющее в пределах камеры сбросной и турбинный потоки.

В. И. Синотин [225] на основании проведенных исследований эжекторной балки на довольно крупной модели (ширина лотка 0,73 м) без турбины утверждает, что эжектирование с применением балки повышает «паводочный напор ГЭС до 40%, т. е. оно примерно в два раза эффективней эжекции при пропуске паводка любой обеспеченности» [225, стр. 191]. Экспериментальные данные подтверждаются им расчетами по формуле эффекта эжекции с учетом перепада восстановления за балкой. Но величина эффекта эжекции В. И. Синотиным завышена, а его формула весьма приближенна, поскольку он исходил из гидростатического распределения давления в выходном сечении отсасывающей трубы и считал, что эффект эжекции определяется разностью уровней свободной поверхности нижнего бьефа за балкой и перед ней. В действительности пьезометрические напоры под водосбросной струей и над ней различны, что необходимо учитывать при введении в расчетную схему сил давления в начальном сечении и на наклонный участок водобоя. Совпадение расчетных и опытных точек обеспечено надлежащим подбором входящих в формулу коэффициента ε=h/t и «коэффициента восстановления напора» η в формуле Борда, использованной для определения перепада восстановления за балкой (строго говоря, неприменимой к открытым потокам).
Придание кромке балки обтекаемых форм, т. е. устройство козырька, подобного рассмотренному для диффузорной камеры, может обеспечить увеличение разности уровней свободной поверхности до балки и за ней в 1,7 раза. Максимальная разность указанных уровней была получена при заложении наклонного участка водобоя 2—2,5 и расположении балки в створе окончания наклонного участка.
Автор рассматриваемой работы рекомендует применять эжекторные балки для увеличения расхода через затопленные отверстия различных сооружений. В этом случае конструкция концевого участка водосброса представляет собой диффузорную камеру, расчет которой можно производить по формулам гл. 7.

д) Эжекция при сопряжении бьефов свободной отброшенной струей

 Как показывают опыты и теоретический анализ явления, при сопряжении бьефов свободной отброшенной струей уровень под струей устанавливается в зависимости от параметров потока и сооружения выше или ниже уровня в отводящем русле за местом падения струи. В последнем случае напор турбины увеличивается, т. е. отброшенная струя оказывает на турбинный поток эжектирующее влияние. Оценка влияния сброса паводка на уровень под струей необходима прежде всего для правильного назначения высотного положения некоторых элементов здания ГЭС, а также для определения высоты отсасывания в целях оценки возможности появления кавитационных режимов работы турбин.

Для плоской задачи расчет уровня свободной поверхности под свободной отброшенной струей дан [25] в связи с определением уровня нижнего бьефа в отводящем русле, при котором возможно появление неустойчивости струи в виде ее биения в вертикальной плоскости. Это  расчет уровня свободной поверхности под струей с учетом перечисленных факторов затруднителен вследствие отсутствия возможности их достаточно достоверного учета. Расчет без учета влияния аэрации струи и ее распаде возможен, но его результаты не могут быть признаны достаточно надежными вследствие отсутствия их проверки по данным натурных наблюдений. По-видимому, чем меньше дальность отлета струи, тем большую достоверность имеют результаты расчета. Для схемы, изображенной на рис. 8-4, превышение сливной кромки уступа над уровнем воды под струей может быть определено, разумеется приближенно, по по формулам (8-5'), (8-6'), где по-прежнему
Эти формулы получены в предположении, что уровни в поперечных сечениях в створе уступа и за местом падения струи постоянны по сечению, чего нет в действительности.
Эффект эжекции при сопряжении бьефов свободно отброшенной струей зафиксирован натурными наблюдениями на Высотной Асуанской плотине1. При Нст= 48 м, работающих турбинах и водосбросах четырех турбинных блоков (—750 м³/сек) зафиксирована при полном открытии отверстий (1 600 м/сек) разность уровней в створе за местом падения струи и в створе отверстия отсасывающих труб, равная 1,1 м. При открытии двух отверстий полностью, а двух на 0,48 от полного (1 080 м³/сек) разность уровней в указанных створах равна 0,9 м.
Поскольку при неработающих водосбросах в отводящем русле здания явление в натуре возможно только тогда, когда под  струей за уступом образуется воздушная полость.
Сопоставление расчетов с опытными данными, проведенное автором предложенной зависимости, дало вполне приемлемые результаты. В натурных условиях образование воздушной полости под струей может быть только при длинных низовых быках и большом наклоне струи в сторону нижнего бьефа при сходе ее с консоли (на ГЭС типа Плявиньской) или с уступа. Но поскольку неустойчивость струи недопустима, воздушная полость под струей для срыва вакуума не должна быть замкнутой.
Применяя к отсеку нижнего бьефа со свободно отброшенной струей уравнение количества движения, получаем те же зависимости, что и для расчета пьезометрического напора под водосбросной струей при свободном доступе воздуха под струю. Однако вследствие аэрации струи на сливе, распада струи и дальнейшего насыщения ее воздухом в свободном падении необходимо в расчет вводить объемный вес, глубину и скорость воды с учетом насыщения струи воздухом. Следует также учитывать расширение струи в плане на водосливе. Неопределенность в такой расчет вносит трудность учета действительного распределения скоростей в сечении за местом падения струи, особенно в связи с тем, что ширина нижнего бьефа обычно больше ширины струи в плане.

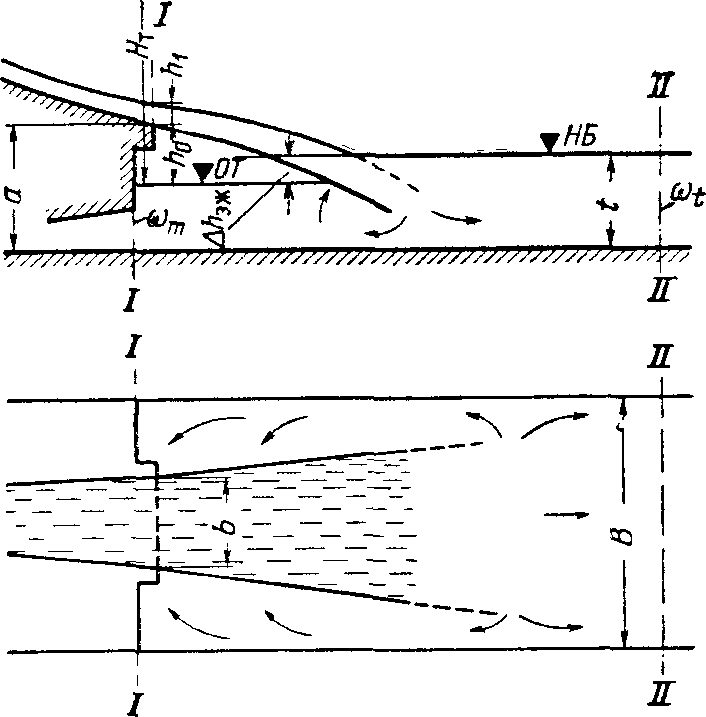
Рис. 8-4. К расчету эжекции при сопряжении бьефов свободно отброшенной струи.
Данные любезно предоставлены Директором Департамента водохранилища Высотной Асуанской плотины доктором инж. Камаль Юзефом Камаль.

ГЭС наблюдается подпор 0,15—0,20 м, пьезометрический эффект эжекции в рассматриваемых случаях равен 1,25—1,3 м и 1,05—1,1 м.
При открытии всех водосбросов ожидается согласно исследованиям пространственной модели Асуанской ГЭС понижение уровня в створе отверстий отсасывающих труб на величину порядка 3 м. Но поскольку при одновременной работе турбин и водосбросов потери напора в подводящем туннеле существенно возрастают, напор турбины за счет эжекции не увеличивается, а лишь частично восстанавливается, т. е. за счет эжекции может компенсироваться часть потерь напора в подводящем тракте. В данном случае возможность восстановления мощности не будет использоваться, так как потери напора могут компенсироваться увеличением расхода турбин за счет большего открытия направляющего аппарата.

е) Влияние на эффект эжекции свободного доступа воздуха под водосбросную струю

При донных режимах в случае низовых быков, значительно выдвинутых в нижний бьеф, возможно образование под струей вакуума, что недопустимо вследствие его отрицательного влияния на эффект эжекции, неустойчивости струи (§ 6-14) и динамических ударов при срыве вакуума.
То, что образование под струей вакуума снижает напор турбины, кажется противоречащим здравому смыслу. Однако это следует из экспериментальных данных (рис. 8-5) и анализа уравнения количества движения.
Рассмотрим отсек нижнего бьефа при постоянных расходах QT и QB в двух случаях: при наличии и отсутствии воздушной полости под струей (рис. 8-6,а, б). На рис. 8-6,б полость заполнена водой за счет вакуума под струей, образовавшегося в результате захвата струей воздуха.

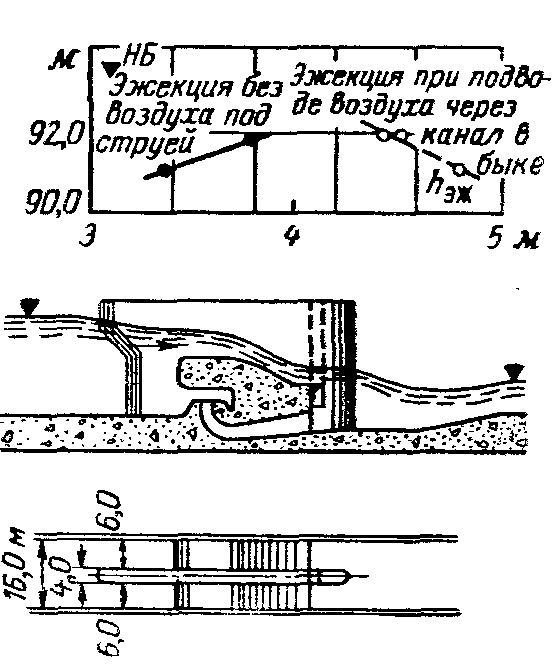
Рис. 8-5. Результаты опытов на модели Камской водосливной ГЭС, показывающие влияния вакуума под струей на эффект эжекции (опыты автора).
Уравнения количества движения, составленные для отсеков нижнего бьефа, для двух случаев отличаются лишь выражением импульсов сил в створе уступа, которые вследствие равенства остальных членов уравнений должны быть равны, т. е. смотрении эпюр давления на рис. 8-6. С появлением отрицательной части эпюры на рис. 8-6,б положительная часть эпюры давления на уступ увеличивается (сумма площадей постоянна), что уменьшает hоб (уменьшает напор турбины).


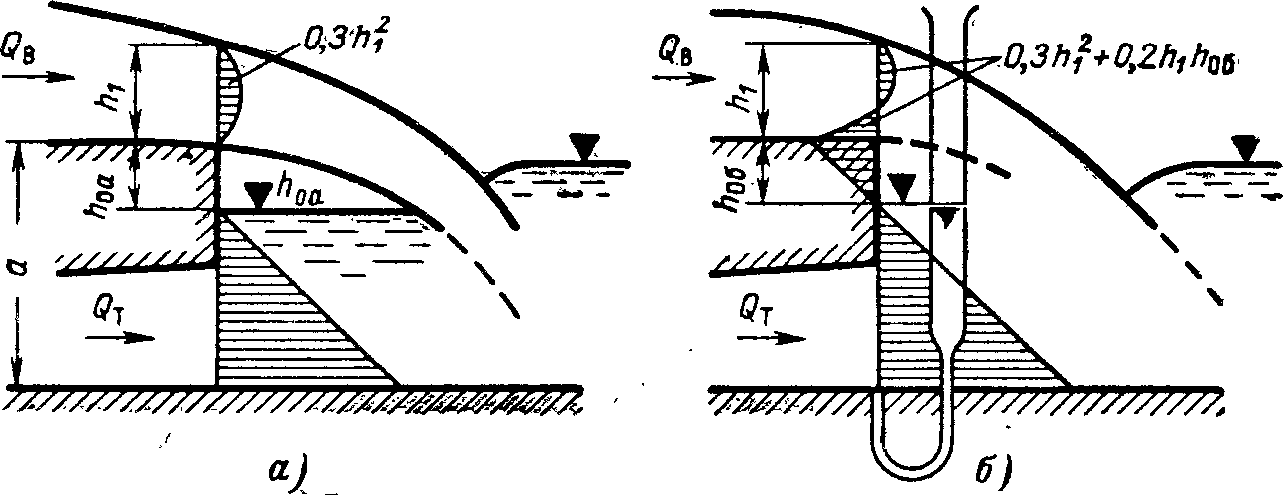
Рис. 8-6. К оценке влияния вакуума под струей на напор турбины при эжекции.
а — под струей воздушная полость; б — в результате образования вакуума воздушная полость под струей заполнена водой.